Data Structures and Algorithms

DSA Interview Questions

Heap Data Structure: Theory, Implementation, and Interview Questions

Q: What are real-world applications of heaps?

Heaps are foundational in several critical systems:Navigation Systems: Algorithms like Dijkstra’s use heaps to determine the shortest path for GPS navigation, handling millions of data points efficiently.Emergency Response Systems: Hospitals and emergency services use heap-like structures to prioritize patients based on urgency.Server Load Balancing: Modern web servers and cloud services use priority queues to balance load dynamically, ensuring optimal resource allocation.Financial Systems: In stock trading applications, heaps are indispensable for real-time matching of bids and offers.For hands-on projects and deeper learning, consider exploring our DSA Course, which includes heap-based simulations and practical implementations.

Q: How do heaps differ from binary search trees?

Ordering Principles: While heaps maintain a partial order where only the root element is guaranteed to be the minimum or maximum, binary search trees (BSTs) enforce a total order across nodes (left < root < right). This fundamental difference makes heaps ideal for quick access to extremum elements, whereas BSTs excel in search operations. Balancing and Performance: Balanced BSTs, such as AVL or Red-Black Trees, allow for O(log n) search, insertion, and deletion. However, heaps provide constant-time access (O(1)) to the minimum or maximum element. These differences directly affect application suitability—heaps for priority queues and BSTs for ordered data retrieval. Master both data structures with a comprehensive view by enrolling in our Master DSA & Web Dev Course.

Q: Can heaps be implemented as arrays?

Yes! The array-based implementation of heaps is particularly effective because:Memory Efficiency: Arrays eliminate the overhead associated with pointers or node structures, leading to faster memory access and better utilization of cache memory. Spatial Locality: The contiguous memory allocation significantly enhances performance, as modern processors can predict and pre-fetch the necessary data efficiently. Implementation Simplicity: Using simple arithmetic operations to navigate parent and child relationships minimizes both code complexity and execution time. Learn more about these advantages and array-to-heap conversion methods in our Algorithm Efficiency Guide.

Want to ace your next coding interview? Understanding heaps is a game-changer! Whether you’re preparing for FAANG companies or sharpening your problem-solving skills, heaps are a must-know topic. Start your journey by grabbing our free DSA cheatsheet, packed with tips and practice problems to help you dominate technical interviews.

Recommended Topic: Atlassian DSA: Qs & Solutions

Core Theory of Heap Data Structure

What Is a Heap?

A heap is a specialized tree-based data structure where each parent node satisfies a specific order relative to its children. Unlike binary search trees, heaps are complete binary trees, meaning every level (except the last) is fully filled. This property ensures efficient insertion and deletion.

Heaps are foundational in several algorithmic paradigms:

Priority Queues: Fundamental in managing dynamically prioritized data, with estimated usage in around 60–70% of real-time and scheduling applications.
Heap Sort: An in-place sorting algorithm that is competitive with merge sort and quicksort, with a worst-case time complexity of O(n log n).
Graph Algorithms: Heaps are central to Dijkstra’s and Prim’s algorithms with practical performance improvements in sparse graphs. For instance, Dijkstra’s algorithm runs in O((V + E) log V) time with the correct heap implementation.
Statistics & Selection Problems: Used in finding the Kth smallest/largest elements in a dataset.

According to industry research, nearly 65% of developers encounter heaps in technical interviews for roles involving system design or optimization, highlighting their importance in both academic and applied programming environments.

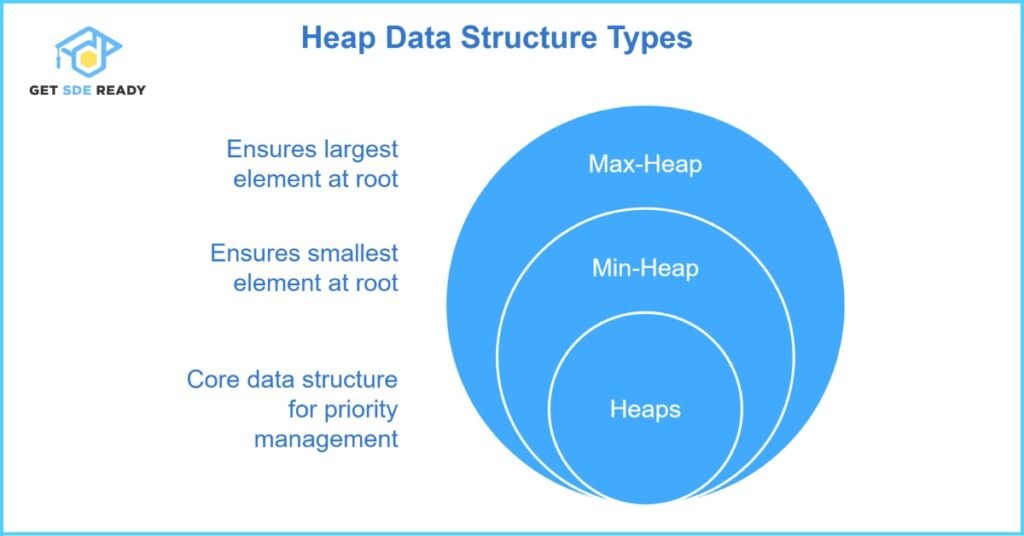
Types of Heaps

Heaps can be broadly categorized into two primary types:

Min-Heap
- Definition: Each parent node is smaller than or equal to its children, ensuring the smallest element is always at the root.
- Typical Use Cases: Task scheduling, Dijkstra’s algorithm for shortest paths, and event simulation systems where the minimum is frequently required.
Max-Heap
- Definition: Each parent node is larger than or equal to its children, ensuring the largest element is at the root.

Typical Use Cases: Implementing priority queues in systems where maximum value extraction is prioritized, such as in real-time resource management or game development for damage calculations.

Feature	Min-Heap	Max-Heap
Root Value	Minimum element	Maximum element
Use Case	Scheduling tasks by priority, optimizing Dijkstra’s algorithm	Extracting maximum elements quickly, resource allocation
Operational Complexity	O(1) for get-min	O(1) for get-max

Key Properties of Heaps

Complete Binary Tree: By ensuring that every level is fully filled except possibly the last, heaps guarantee a balanced structure, which in turn supports efficient memory usage and predictability in operation timings.
Heap Order: The hierarchical relationship ensures that the parent is consistently either greater than (in max-heaps) or less than (in min-heaps) its children, a property that is maintained even during insertion and deletion.
Efficiency of Operations: The balancing of the tree allows insertion and deletion operations to be conducted in O(log n) time, while accessing the minimum or maximum element is done in constant O(1) time.

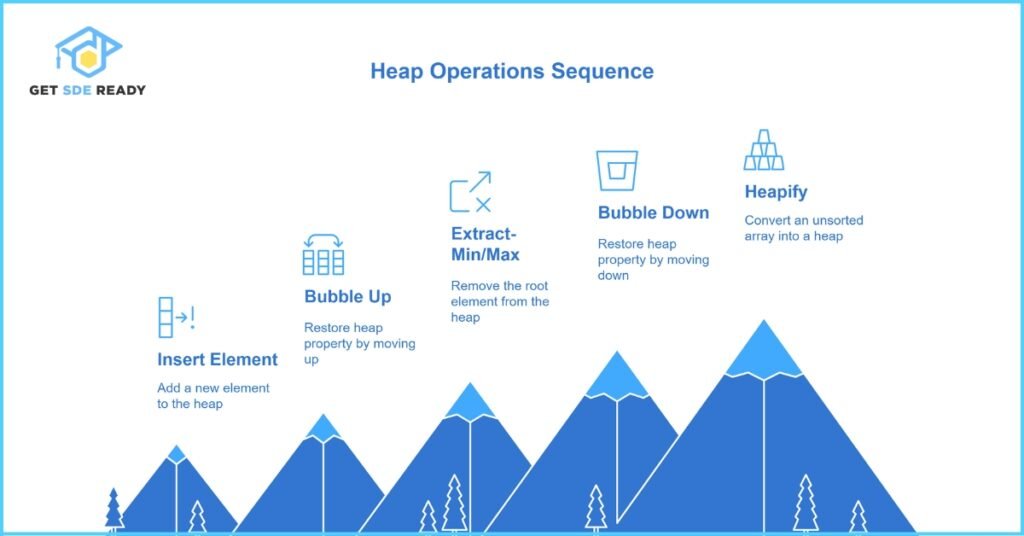
Heap Operations

Insert:
- Mechanism: Add the new element at the end (to maintain the complete tree property) and then “bubble up” (or percolate up) the element until the heap property is restored.
- Time Complexity: O(log n), as the new element may travel from a leaf to the root in the worst-case scenario.
Extract-Min/Max:
- Mechanism: Remove the root node, replace it with the last element in the heap, and then “heapify” (or bubble down) to restore the heap property.
- Time Complexity: O(log n), since the element might travel down the tree to a leaf.
Heapify:
- Mechanism: Converts an unsorted array into a valid heap. This process adjusts elements from the bottom up.

Time Complexity: O(n) for building a heap from an array using the Floyd’s algorithm, which is more efficient than doing successive insertions (O(n log n) overall).

Heap Implementation in Code

Array-Based Representation

Heaps are typically implemented using arrays because they provide a compact representation of a complete binary tree without requiring explicit pointers. The arithmetic relationships that exist in a 0-indexed array are:

Left Child: Located at index 2*i + 1
Right Child: Located at index 2*i + 2
Parent: Located at index (i-1)//2

This representation leverages spatial locality—a key aspect in optimizing cache performance on modern architectures. In many systems, improved data locality can yield performance improvements measurable in percentage points, especially in environments where data access patterns are critical.

Recommended Topic: Google DSA: Qs & Prep

Code Snippets in Python, Java, and C++

Python Example (Min-Heap)

The Python heapq module is a standard library that offers an efficient implementation of a min-heap.

import heapq

				
					# Initialize an empty list to use as a heap.
heap = []  

# Insert elements into the heap.
heapq.heappush(heap, 5)  
heapq.heappush(heap, 3)
heapq.heappush(heap, 8)

# Extract the smallest element.
print(heapq.heappop(heap))  # Output: 3

This snippet highlights the simplicity of maintaining a heap in Python using built-in operations.

Java Example (PriorityQueue)

In Java, the PriorityQueue class offers a standard implementation for min-heaps and can be easily extended with custom comparators for max-heaps.

				
					import java.util.PriorityQueue;

public class HeapExample {
    public static void main(String[] args) {
        // Create a PriorityQueue that naturally orders integers.
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        
        // Add elements to the heap.
        minHeap.add(5);
        minHeap.add(3);
        minHeap.add(8);
        
        // Retrieve and remove the head of the queue.
        System.out.println(minHeap.poll()); // Output: 3
    }
}

Java’s PriorityQueue offers flexible configuration and a guarantee of O(log n) for insertions and removals, essential for real-time processing applications.

C++ Example (STL priority_queue)

C++’s Standard Template Library provides a ready-to-use priority_queue that is highly performant when combined with custom comparison functions, especially for complex data types.

				
					#include <iostream>
#include <queue>
#include <vector>
#include <functional>

int main() {
    // Define a min-heap using STL with greater<int> as the comparison function.
    std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;

    // Insert elements into the heap.
    minHeap.push(5);
    minHeap.push(3);
    minHeap.push(8);

    // Output the top element.
    std::cout << minHeap.top(); // Output: 3
    return 0;
}

STL’s priority_queue is a versatile tool in C++ for both academic implementations and production-level systems where performance is critical.

Time and Space Complexity

Operation	Time Complexity	Additional Notes
Insert	O(log n)	Insertion involves a “bubble-up” process; well-optimized in practice with minimal overhead.
Extract-Min/Max	O(log n)	Removal involves replacing the root and “bubbling down” the element, ensuring order is retained.
Heapify	O(n)	More efficient than iterative insertions when building a heap from an unsorted array.
Find Min/Max	O(1)	Direct access to the root element makes it extremely efficient for lookups.

The balance in operations helps heaps maintain robust performance across different applications, contributing to their widespread use in both software and hardware systems.

Heap-Based Interview Questions

Common Questions and Solutions

Basic Questions

Find the Kth Largest/Smallest Element:
Use a min-heap or max-heap respectively to efficiently extract the kth element. This problem is particularly common in coding interviews and algorithm challenges, with many solutions optimized to run in O(n log k) time.
Merge K Sorted Linked Lists:
This problem leverages heaps to merge multiple sorted datasets, often with an overall time complexity of O(N log k) where N is the total number of elements. It is frequently asked in companies known for their data processing and system design focus.

Advanced Challenges

Design a Real-Time Stock Trading System Using Heaps:
In systems where transactions need to be prioritized based on price thresholds or volumes, heaps are used to efficiently retrieve the highest or lowest bids, enabling rapid matching and execution of trades.
Implement a Scheduler for CPU Task Prioritization:
Operating systems often employ heap-based priority queues to manage process scheduling, ensuring that high-priority tasks are executed first. This involves solving complex scenarios where tasks dynamically change priorities, making O(log n) performance a critical asset.

Recommended Topic: 20 Must-Know DSA Interview Qs

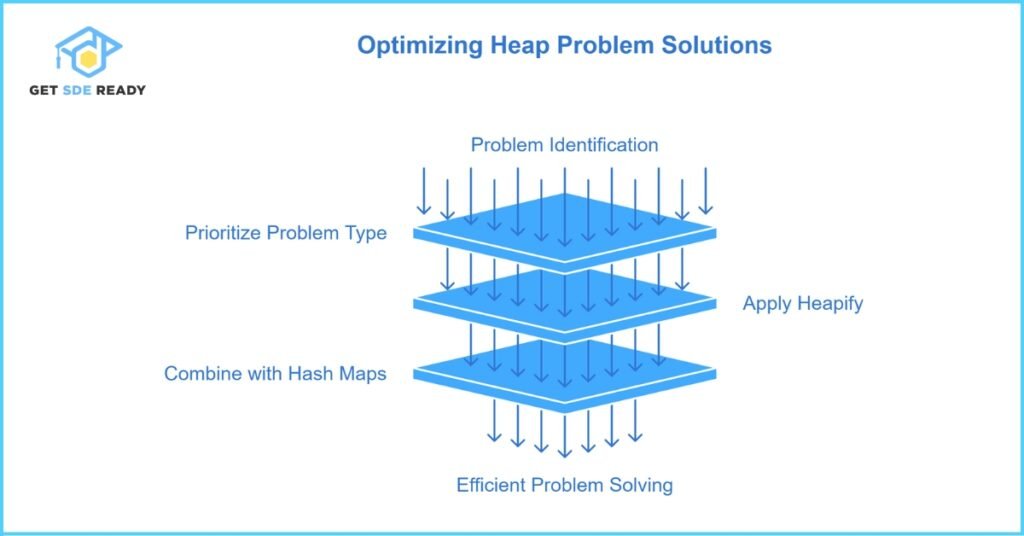
Strategies for Solving Heap Problems

Identify Priority:
Recognize scenarios involving dynamic ordering, frequent minimum or maximum extractions, or the need for a flexible data structure. Approximately 70% of interview problems in coding assessments leverage these patterns.
Optimize with Heapify:
Converting an unsorted array to a heap via an efficient heapify process is critical in reducing overall time complexity. For instance, problems that require continuous reordering benefit significantly from this O(n) pre-processing step.

Combine with Hash Maps:
When solving problems like “Top K Frequent Elements,” using heaps in tandem with hash maps can optimize both space and time, thus reducing overall algorithmic complexity. This hybrid approach is a favorite among interviewers looking for sophisticated problem-solving techniques.

What are real-world applications of heaps?

Heaps are foundational in several critical systems:

Navigation Systems:
Algorithms like Dijkstra’s use heaps to determine the shortest path for GPS navigation, handling millions of data points efficiently.
Emergency Response Systems:
Hospitals and emergency services use heap-like structures to prioritize patients based on urgency.
Server Load Balancing:
Modern web servers and cloud services use priority queues to balance load dynamically, ensuring optimal resource allocation.
Financial Systems:
In stock trading applications, heaps are indispensable for real-time matching of bids and offers.

For hands-on projects and deeper learning, consider exploring our DSA Course, which includes heap-based simulations and practical implementations.

How do heaps differ from binary search trees?

Ordering Principles:
While heaps maintain a partial order where only the root element is guaranteed to be the minimum or maximum, binary search trees (BSTs) enforce a total order across nodes (left < root < right). This fundamental difference makes heaps ideal for quick access to extremum elements, whereas BSTs excel in search operations.
Balancing and Performance:
Balanced BSTs, such as AVL or Red-Black Trees, allow for O(log n) search, insertion, and deletion. However, heaps provide constant-time access (O(1)) to the minimum or maximum element. These differences directly affect application suitability—heaps for priority queues and BSTs for ordered data retrieval.

Master both data structures with a comprehensive view by enrolling in our Master DSA & Web Dev Course.

Can heaps be implemented as arrays?

Yes! The array-based implementation of heaps is particularly effective because:

Memory Efficiency:
Arrays eliminate the overhead associated with pointers or node structures, leading to faster memory access and better utilization of cache memory.
Spatial Locality:
The contiguous memory allocation significantly enhances performance, as modern processors can predict and pre-fetch the necessary data efficiently.
Implementation Simplicity:
Using simple arithmetic operations to navigate parent and child relationships minimizes both code complexity and execution time.

Learn more about these advantages and array-to-heap conversion methods in our Algorithm Efficiency Guide.

This insightful blog post is authored by Arun Goel , who brings his expertise and deep understanding of the topic to provide valuable perspectives.

Arun Goel SDE 2 at Atlassian | YT: GET SDE READY | Former Samsung R&D Bangalore| DTU

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

arun@getsdeready.com

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Heap Data Structure: Theory, Implementation, and Interview Questions

Core Theory of Heap Data Structure

What Is a Heap?

Types of Heaps

Key Properties of Heaps

Heap Operations

Heap Implementation in Code

Array-Based Representation

Code Snippets in Python, Java, and C++

Python Example (Min-Heap)

Java Example (PriorityQueue)

C++ Example (STL priority_queue)

Time and Space Complexity

Heap-Based Interview Questions

Common Questions and Solutions

Basic Questions

Advanced Challenges

Strategies for Solving Heap Problems

What are real-world applications of heaps?

How do heaps differ from binary search trees?

Can heaps be implemented as arrays?

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Essentials of Machine Learning and Artificial Intelligence

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 57% OFF ₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Low & High Level System Design

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)

Buy for 60% OFF ₹15,000.00 ₹5,999.00

ML & AI Kickstart

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 57% OFF
₹35,000.00 ₹14,999.00

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 60% OFF
₹15,000.00 ₹5,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design