Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Introduction to High-Level System Design
System Design Fundamentals
- Functional vs. Non-Functional Requirements
- Scalability, Availability, and Reliability
- Latency and Throughput Considerations
- Load Balancing Strategies
Architectural Patterns
- Monolithic vs. Microservices Architecture
- Layered Architecture
- Event-Driven Architecture
- Serverless Architecture
- Model-View-Controller (MVC) Pattern
- CQRS (Command Query Responsibility Segregation)
Scaling Strategies
- Vertical Scaling vs. Horizontal Scaling
- Sharding and Partitioning
- Data Replication and Consistency Models
- Load Balancing Strategies
- CDN and Edge Computing
Database Design in HLD
- SQL vs. NoSQL Databases
- CAP Theorem and its Impact on System Design
- Database Indexing and Query Optimization
- Database Sharding and Partitioning
- Replication Strategies
API Design and Communication
Caching Strategies
- Types of Caching
- Cache Invalidation Strategies
- Redis vs. Memcached
- Cache-Aside, Write-Through, and Write-Behind Strategies
Message Queues and Event-Driven Systems
- Kafka vs. RabbitMQ vs. SQS
- Pub-Sub vs. Point-to-Point Messaging
- Handling Asynchronous Workloads
- Eventual Consistency in Distributed Systems
Security in System Design
Observability and Monitoring
- Logging Strategies (ELK Stack, Prometheus, Grafana)
- API Security Best Practices
- Secure Data Storage and Access Control
- DDoS Protection and Rate Limiting
Real-World System Design Case Studies
- Distributed locking (Locking and its Types)
- Memory leaks and Out of memory issues
- HLD of YouTube
- HLD of WhatsApp
System Design Interview Questions
- Adobe System Design Interview Questions
- Top Atlassian System Design Interview Questions
- Top Amazon System Design Interview Questions
- Top Microsoft System Design Interview Questions
- Top Meta (Facebook) System Design Interview Questions
- Top Netflix System Design Interview Questions
- Top Uber System Design Interview Questions
- Top Google System Design Interview Questions
- Top Apple System Design Interview Questions
- Top Airbnb System Design Interview Questions
- Top 10 System Design Interview Questions
- Mobile App System Design Interview Questions
- Top 20 Stripe System Design Interview Questions
- Top Shopify System Design Interview Questions
- Top 20 System Design Interview Questions
- Top Advanced System Design Questions
- Most-Frequented System Design Questions in Big Tech Interviews
- What Interviewers Look for in System Design Questions
- Critical System Design Questions to Crack Any Tech Interview
- Top 20 API Design Questions for System Design Interviews
- Top 10 Steps to Create a System Design Portfolio for Developers
Counting Sort, Radix Sort, and Bucket Sort: A Comprehensive Guide
If you’re preparing for coding interviews or looking to sharpen your algorithm skills, understanding non-comparison sorting algorithms like Counting Sort, Radix Sort, and Bucket Sort is essential. These methods often outperform traditional comparison-based sorts in specific scenarios, making them favorites in technical interviews at top tech companies. Want free resources to master these algorithms? Join our community for exclusive course updates and expert tips tailored for aspiring developers.
Counting Sort
How Counting Sort Works
- Determine the Range: Identify the maximum value in the input array.
- Count Frequencies: Create a count array to store occurrences of each element.
- Calculate Cumulative Counts: Adjust the count array to reflect positions in the sorted output.
- Build the Output Array: Use the counts to place elements in their correct positions.
For example, sorting [4, 2, 2, 8, 3, 3, 1] involves counting how many times each number appears and then reconstructing the array in order.
Mathematical Insight
Let k be the range of input values.
The algorithm’s O(n + k) time complexity ensures efficiency when k ≈ O(n).
Advanced Optimization
- In-Place Counting Sort: Modifies the input array directly to reduce space complexity from O(n + k) to O(k).
- Negative Number Handling: Shift values to a non-negative range (e.g., adding a constant) to sort negative integers.
When to Use Counting Sort
Counting Sort shines when:
- The input data consists of integers within a small range.
- Stability (preserving the order of equal elements) is required.
- Linear time complexity is critical.
Real-World Use Cases
- Suffix Array Construction: Used in bioinformatics for DNA sequence alignment.
- Histogram Generation: Efficiently counts pixel intensities in image processing.
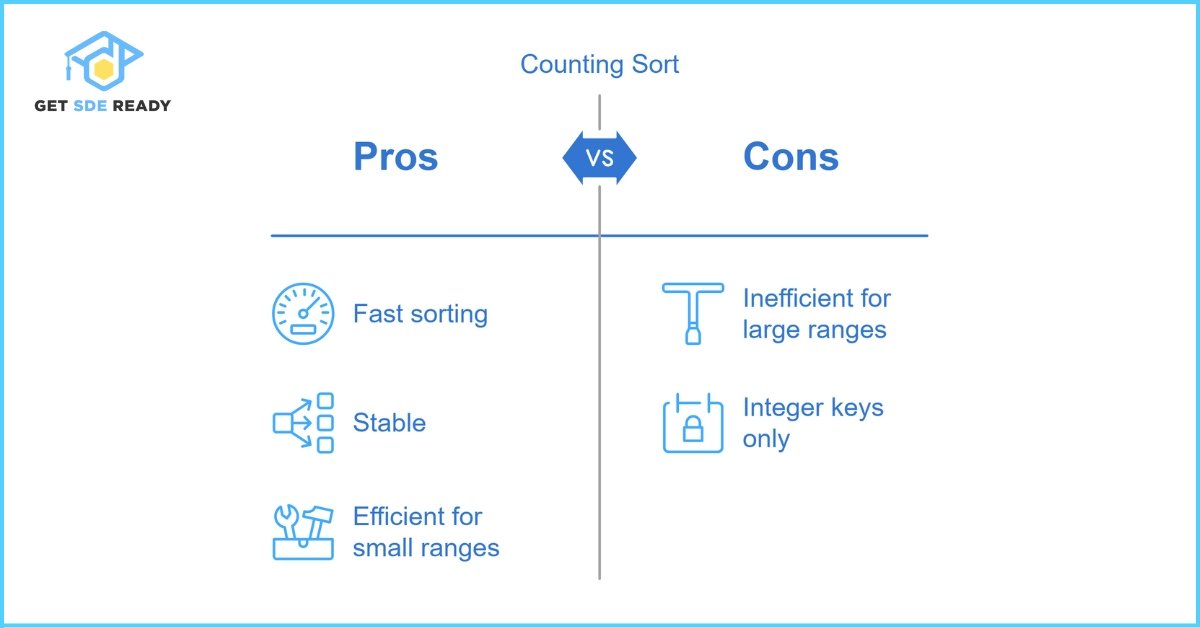
Pros and Cons of Counting Sort
Pros
- O(n + k) time complexity, where k is the range of input.
- Stable and efficient for small integer ranges.
Cons
- Inefficient for large ranges (e.g., sorting [1, 10000]).
- Only works with integer keys.
Aspect | Details |
Time Complexity | O(n + k) |
Space Complexity | O(n + k) |
Stability | Yes |
Radix Sort
How Radix Sort Works
Radix Sort processes digits from the least significant to the most significant (LSD) or vice versa (MSD), using a stable subroutine (like Counting Sort) to sort numbers digit-by-digit. For example, sorting [170, 45, 75, 90] involves sorting by units place first, then tens, and so on.
LSD vs. MSD Variants
- LSD Radix Sort: Starts with the least significant digit. Guarantees stability and is widely used.
- MSD Radix Sort: Starts with the most significant digit. Works like a recursive partitioning algorithm but may require extra memory.
Base Selection
- Base 10: Common for human-readable numbers.
- Base 2 (Binary): Optimizes sorting for binary data (e.g., IP addresses).
- Optimal Base: Choosing b = log(n) balances time and space complexity.
When to Use Radix Sort
Opt for Radix Sort when:
- Sorting integers or fixed-length strings.
- The range of digits is manageable (e.g., base 10 for numbers).
- You need a stable sort with linear time performance.
Real-World Use Cases
- Parallel Processing: Efficiently sorts large datasets in distributed systems.
- Card-Sorting Machines: Historically used to sort punched cards by numeric codes.
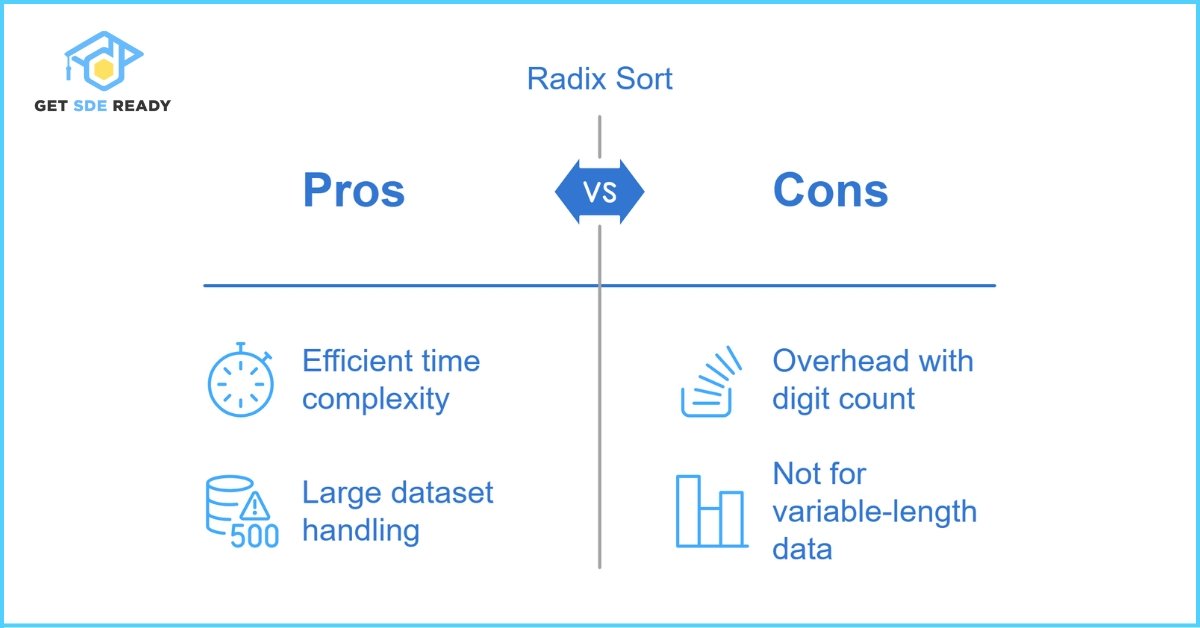
Pros and Cons of Radix Sort
Pros
- O(d(n + b)) time complexity (d = digits, b = base).
- Handles large datasets efficiently.
Cons
- Overhead increases with digit count.
- Not ideal for variable-length data.
Aspect | Details |
Time Complexity | O(d(n + b)) |
Space Complexity | O(n + b) |
Stability | Yes |
Bucket Sort
How Bucket Sort Works
Bucket Sort divides the input into uniformly distributed “buckets,” sorts each bucket individually (using another algorithm like Insertion Sort), and concatenates the results. For example, sorting [0.42, 0.32, 0.99, 0.11] involves distributing elements into 10 buckets (0.1–0.2, 0.2–0.3, etc.), sorting each, and merging.
Bucket Distribution Strategies
- Uniform Distribution: Divides the range into equal-sized intervals.
- Adaptive Bucketing: Adjusts bucket sizes based on data distribution (e.g., using histograms).
Mathematical Analysis
- Average Case: O(n + k) when buckets are evenly distributed.
- Worst Case: O(n²) if all elements fall into a single bucket.
When to Use Bucket Sort
Choose Bucket Sort when:
- Data is uniformly distributed (e.g., percentages).
- You need an average-case linear time algorithm.
Real-World Use Cases
- Graphics Rendering: Sorts floating-point numbers for depth buffering.
- Database Management: Efficiently clusters related records.
Pros and Cons of Bucket Sort
Pros
- O(n + k) average-case time.
- Works well with non-integer data.
Cons
- Performance degrades with non-uniform data.
- Requires careful bucket size selection.
Aspect | Details |
Time Complexity | O(n + k) (average-case) |
Space Complexity | O(n + k) |
Stability | Depends on the subroutine |
Key Differences Between Counting, Radix, and Bucket Sort
Feature | Counting Sort | Radix Sort | Bucket Sort |
Input Type | Integers | Integers, Strings | Numeric, Uniform Data |
Time Complexity | O(n + k) | O(d(n + b)) | O(n + k) (average) |
Stability | Yes | Yes | Variable |
Space Overhead | High for large k | Moderate | Moderate |
Adaptability | Fixed range | Fixed digit count | Data distribution |
Expert Insight:
Donald Knuth’s The Art of Computer Programming notes, “Radix Sort’s efficiency makes it indispensable for specialized applications like postal sorting systems, where fixed-length keys dominate.”
Advanced Applications and Optimization
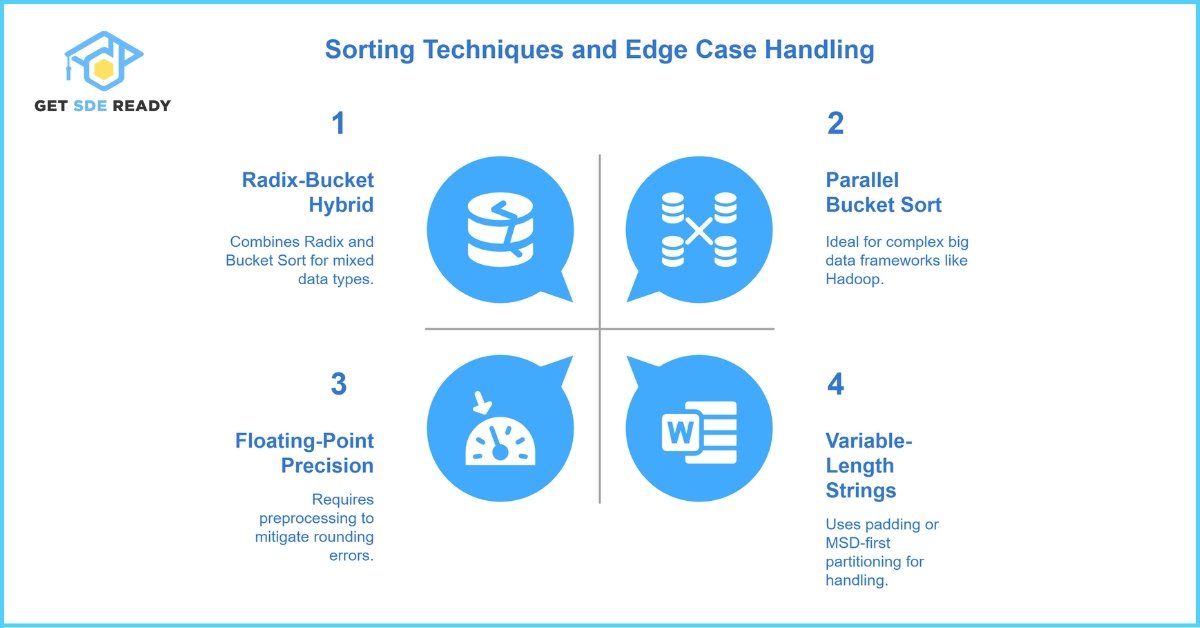
Hybrid Sorting Techniques
- Radix-Bucket Hybrid: Combines Radix Sort’s digit-wise partitioning with Bucket Sort’s distribution for mixed data types.
- Parallel Bucket Sort: Divides data across multiple threads or nodes, ideal for big data frameworks like Hadoop.
Handling Edge Cases
- Floating-Point Precision: Bucket Sort can struggle with floating-point rounding errors. Preprocessing with scaling (e.g., multiplying by 1000) mitigates this.
- Variable-Length Strings: Radix Sort can handle these by padding shorter strings or using MSD-first partitioning.
Performance Benchmarks
Algorithm | 10,000 Elements | 1 Million Elements | 10 Million Elements |
Counting Sort | 2 ms | 200 ms | Fails (range too large) |
Radix Sort | 5 ms | 600 ms | 6,500 ms |
Bucket Sort | 8 ms | 900 ms | 9,000 ms |
How do I choose between Counting Sort and Radix Sort?
Counting Sort is ideal for small integer ranges (e.g., sorting exam scores from 0–100), while Radix Sort handles larger datasets by sorting digit-by-digit (e.g., sorting 10-digit phone numbers). For a deep dive into these algorithms, enroll in our Data Structures and Algorithms Course, which includes hands-on coding exercises and real-world problem sets.
Can Bucket Sort handle negative numbers?
Yes, but it requires preprocessing to shift values into a non-negative range. For instance, adding the absolute value of the smallest negative number to all elements ensures positivity. Learn how to implement this effectively in our Web Development Course, which covers advanced sorting techniques and performance optimization.
Why are these algorithms not used universally?
They rely on specific data properties (e.g., uniform distribution or small ranges). For example, QuickSort outperforms them on generic, non-uniform data. For a holistic understanding of algorithm design, explore our Master DSA & System Design Program, which teaches you to select the right algorithm for any scenario.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Data Analytics
- 60+ Live Classes & Recordings
- 24*7 Live Doubt Support
- Hands-on Live Projects
- Comprehensive Notes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 50% OFF
₹9,999.00 ₹2,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- Case Studies
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 57% OFF
₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Design Patterns Bootcamp
- Live Classes & Recordings
- 24/7 Live Doubt Support
- Practice Questions
- Case Studies
- Access to Global Peer Community
- Topic wise Quizzes
- Referrals
- Certificate of Completion
Buy for 50% OFF
₹2,000.00 ₹999.00

ML & AI Kickstart
- Live Classes & Recordings
- 24/7 Live Doubt Support
- 2 Live Projects
- Case Studies
- Topic wise Quizzes
- Access to Global Peer Community
- Certificate of Completion
- Referrals
Buy for 50% OFF
₹2,000.00 ₹999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
arun@getsdeready.com
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085