Data Structures and Algorithms

DSA Interview Questions

Depth First Search (DFS) in Graphs: A Complete Guide

Want to master DFS and other essential algorithms used in top tech interviews? Sign up here to get access to free resources and exclusive course updates!

What is Depth First Search (DFS)?

Depth First Search (DFS) is a fundamental algorithm used for traversing or searching tree and graph data structures. Starting from a source node, DFS explores as far along each branch as possible before backtracking. It mimics the behavior of Preorder traversal in trees.

How DFS Works: Core Concept

DFS uses recursion (or an explicit stack) to keep track of visited nodes. To avoid visiting the same node multiple times in cyclic graphs, a visited[] array or set is maintained.

DFS Traversal Example (Using Insertion Order)

Example 1:

Input:

				
					adj = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]

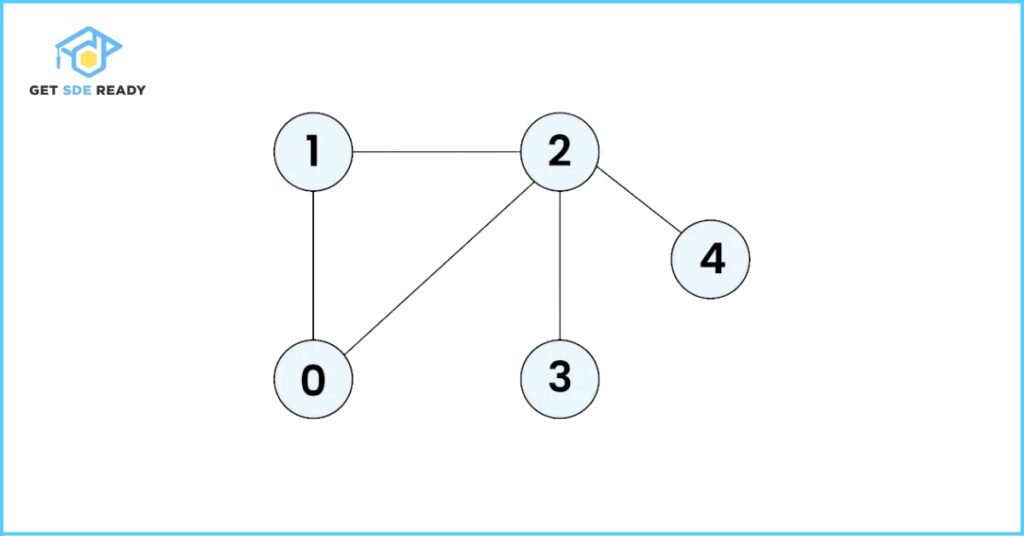
Expected Output:

				
					0 1 2 3 4

Explanation:

Start at node 0 — mark as visited → Output: 0
Move to node 1 → Output: 1
Move to node 2 → Output: 2
Move to node 3 → Output: 3 (backtrack to 2)
Move to node 4 → Output: 4

DFS visits nodes based on the order they appear in the adjacency list, hence multiple valid traversals may exist.

Example 2:

Input:

				
					adj = [[2, 3, 1], [0], [0, 4], [0], [2]]

Expected Output:

0 2 4 3 1

Explanation:

Start at node 0 → mark as visited → Output: 0
Move to node 2 → Output: 2
Move to node 4 → Output: 4
Backtrack to 2 and then to 0
Move to node 3 → Output: 3
Move to node 1 → Output: 1

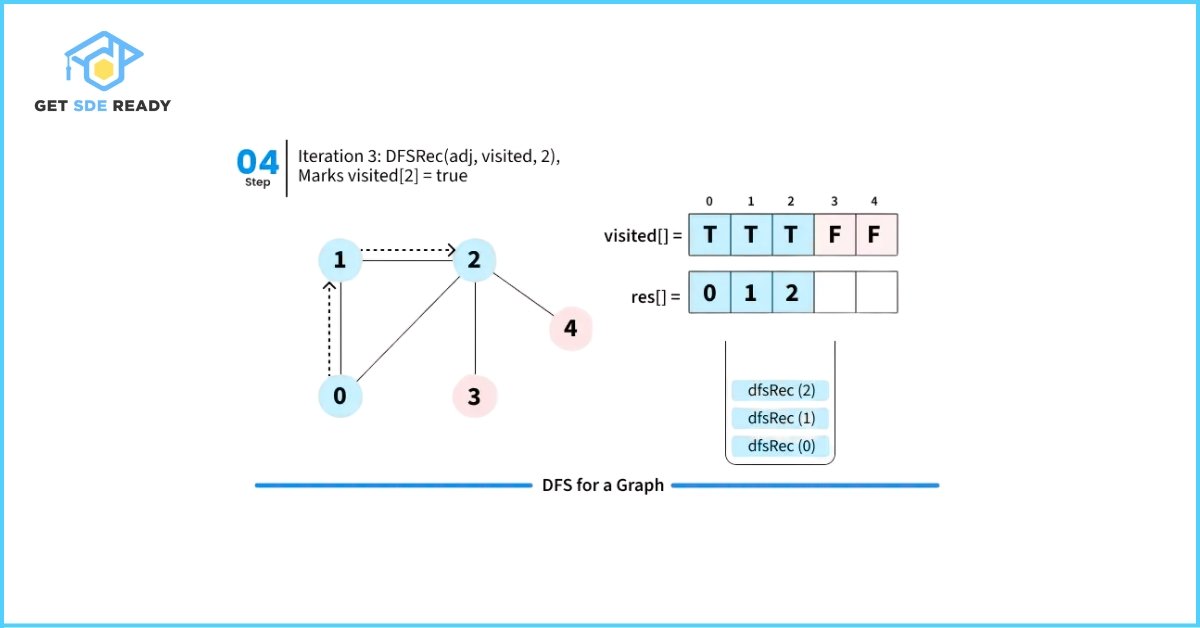
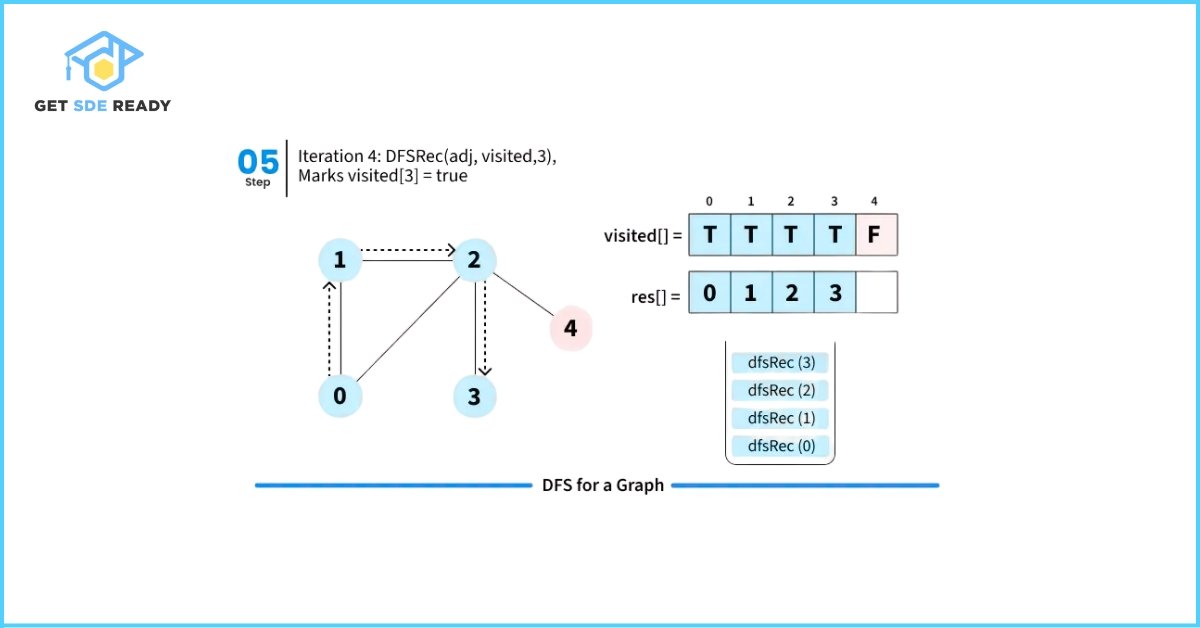
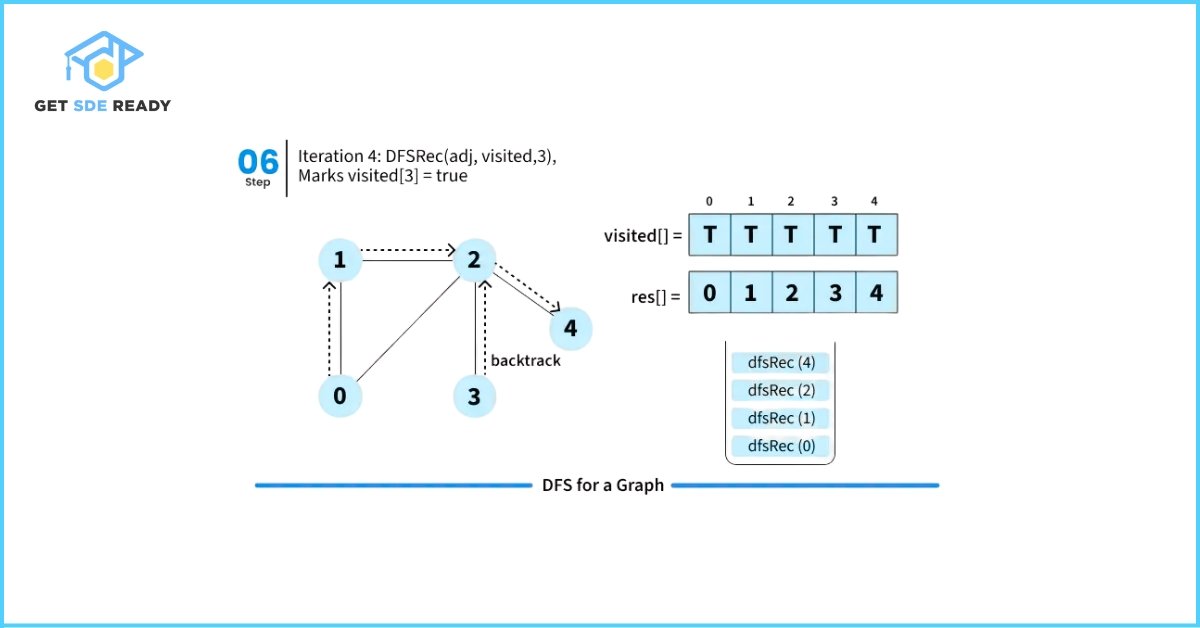
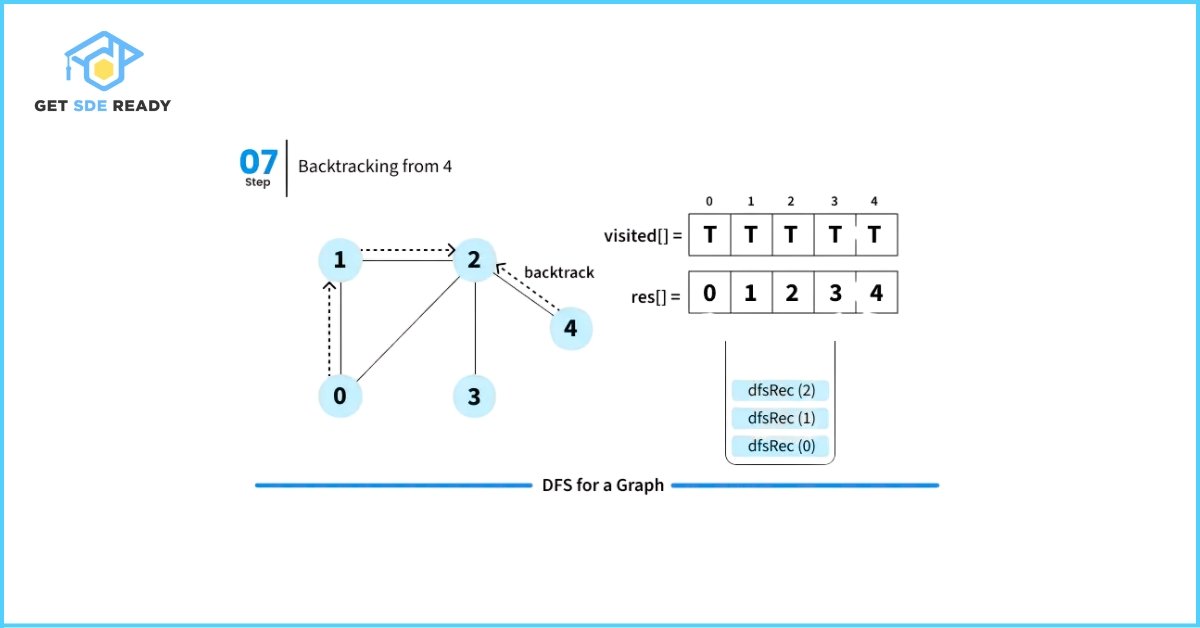
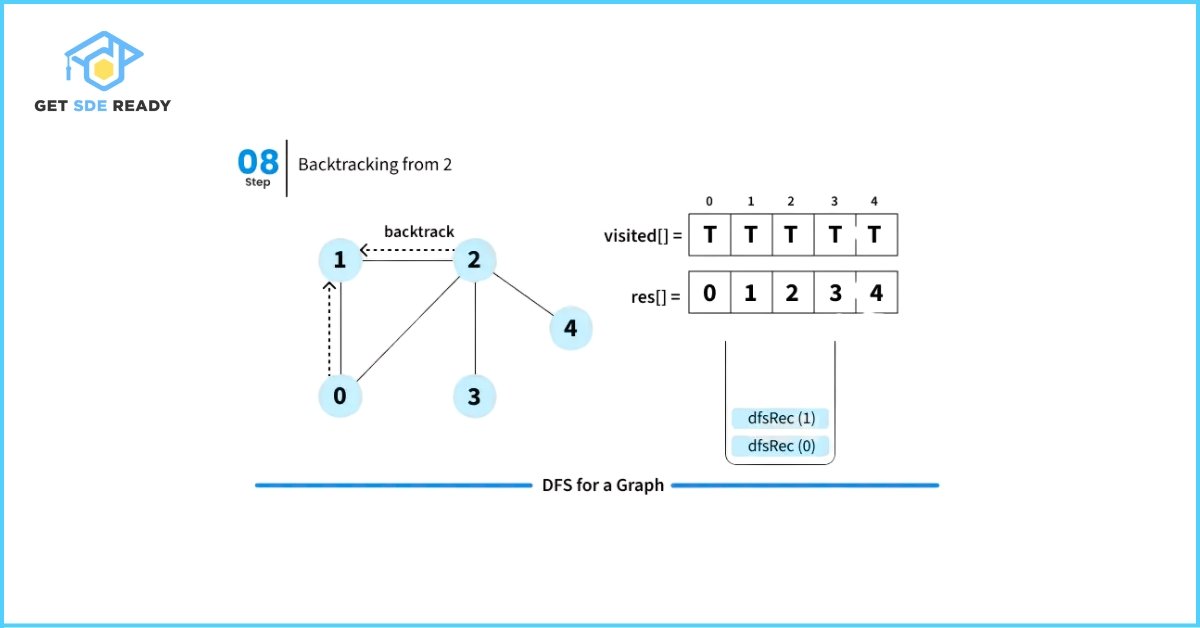
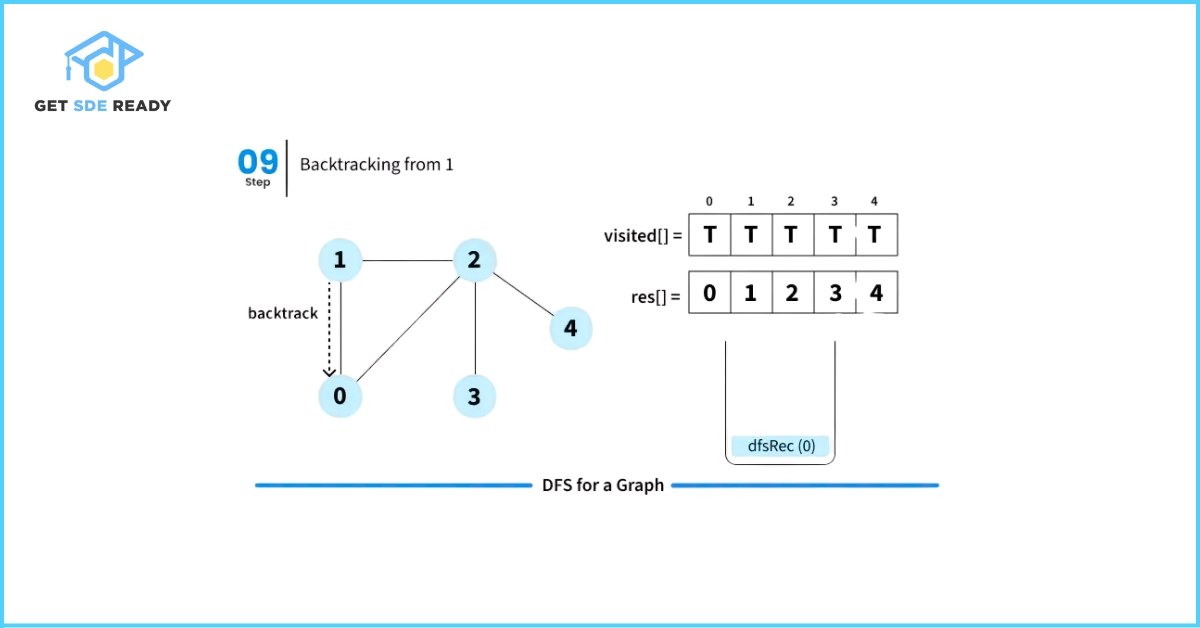
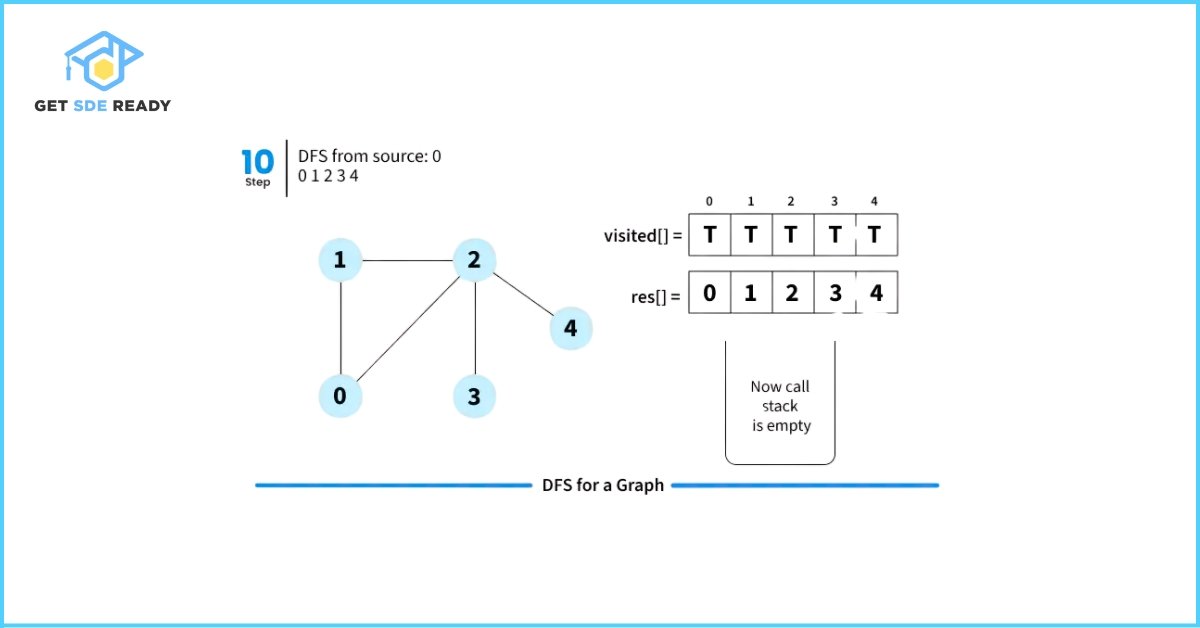
DFS from a Given Source

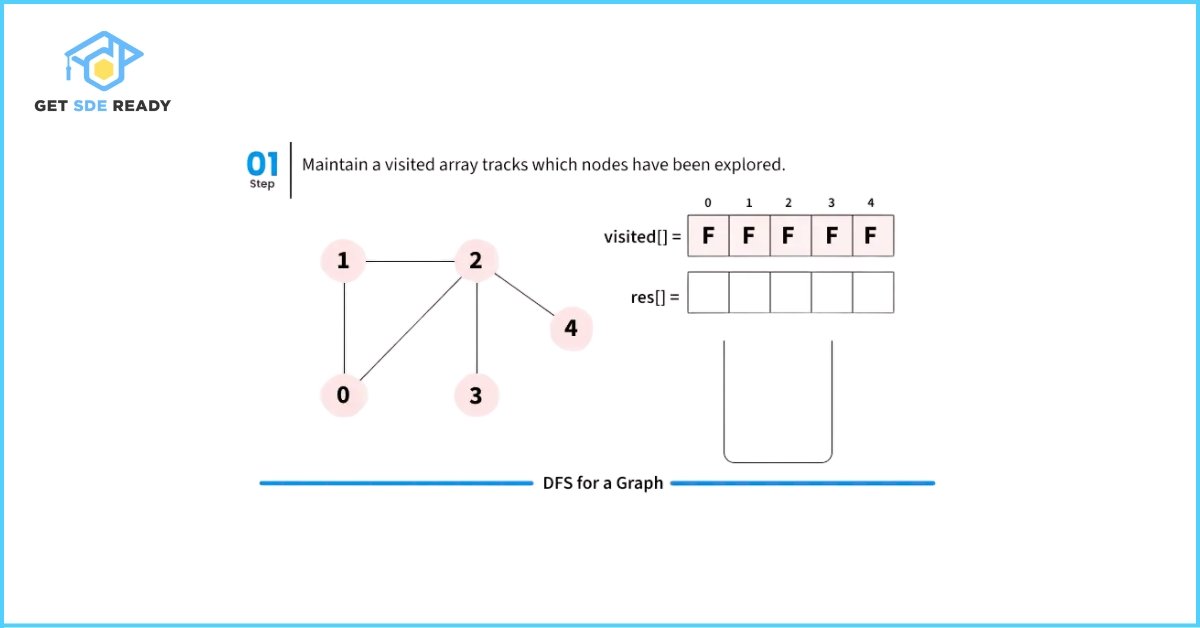
When DFS is initiated from a specific source node in an undirected graph, it visits only those vertices that are reachable from the source.

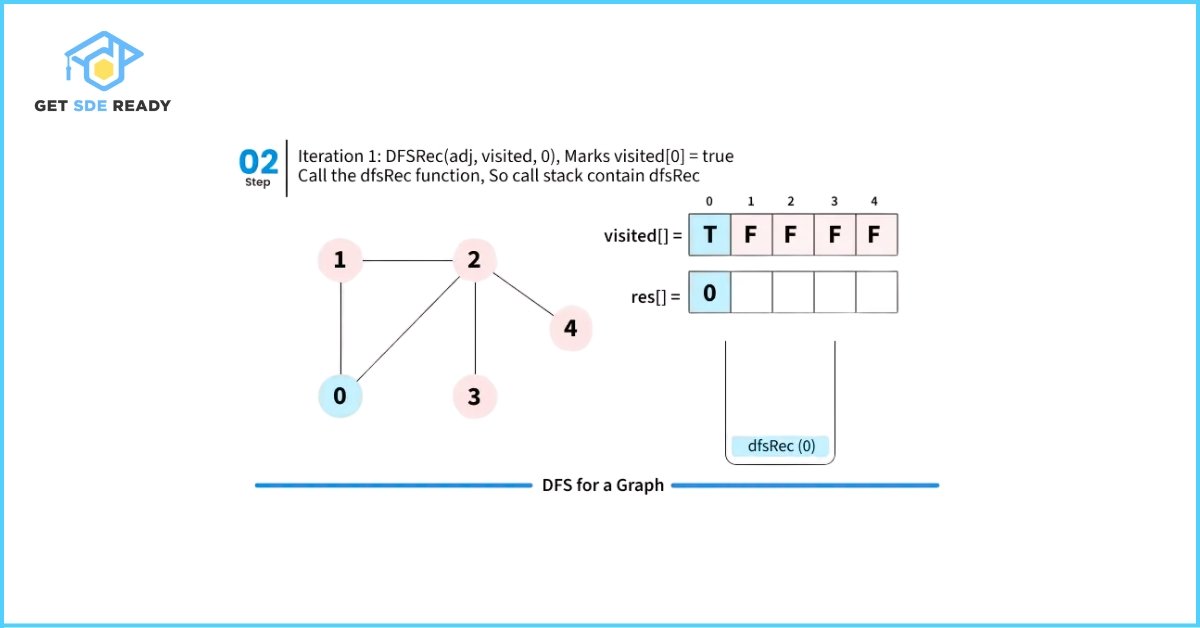
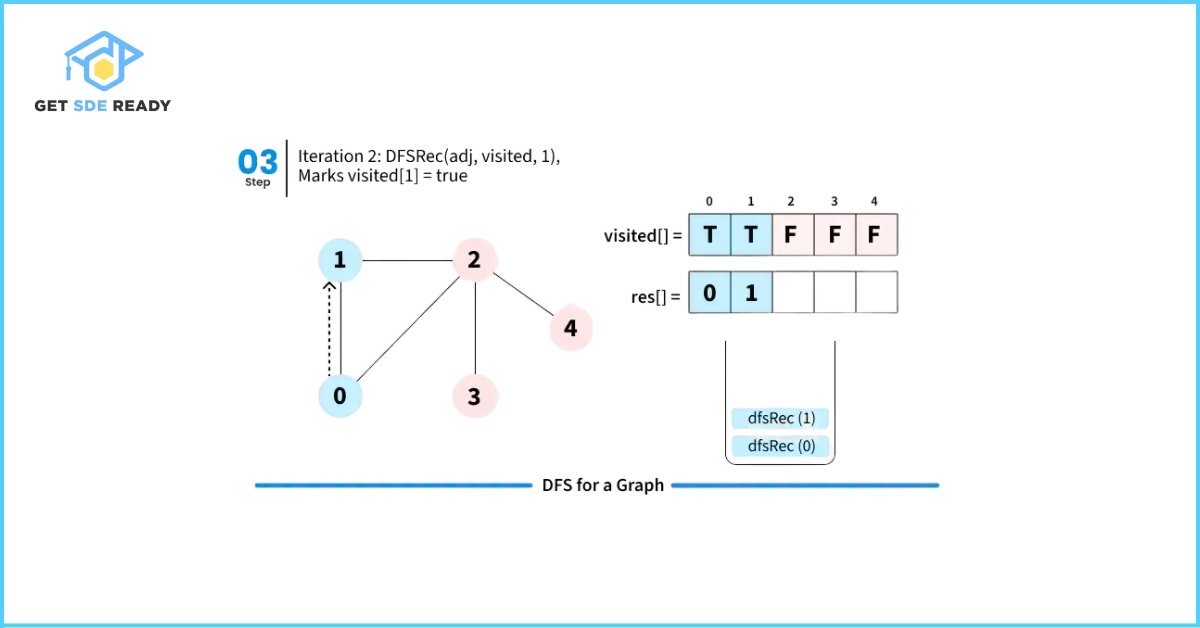
Let’s walk through how Depth First Search (DFS) works with a simple illustration starting from source node 0.

				
					#include <bits/stdc++.h>
using namespace std;

// Recursive function for DFS traversal
void dfsRec(vector<vector<int>> &adj, vector<bool> &visited, int s, vector<int> &res)
{

    visited[s] = true;

    res.push_back(s);

    // Recursively visit all adjacent vertices
    // that are not visited yet
    for (int i : adj[s])
        if (visited[i] == false)
            dfsRec(adj, visited, i, res);
}

// Main DFS function that initializes the visited array
// and call DFSRec
vector<int> DFS(vector<vector<int>> &adj)
{
    vector<bool> visited(adj.size(), false);
    vector<int> res;
    dfsRec(adj, visited, 0, res);
    return res;
}

// To add an edge in an undirected graph
void addEdge(vector<vector<int>> &adj, int s, int t)
{
    adj[s].push_back(t);
    adj[t].push_back(s);
}

int main()
{
    int V = 5;
    vector<vector<int>> adj(V);

    // Add edges
    vector<vector<int>> edges = {{1, 2}, {1, 0}, {2, 0}, {2, 3}, {2, 4}};
    for (auto &e : edges)
        addEdge(adj, e[0], e[1]);

    // Starting vertex for DFS
    vector<int> res = DFS(adj); // Perform DFS starting from the source verte 0;

    for (int i = 0; i < V; i++)
        cout << res[i] << " ";
}

Searching

Traverse the loop to find a target value, requiring safeguards against infinite loops.

For a quick refresher on these operations, try our crash course.

Implementation of Circular Linked Lists

Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.

				
					import java.util.*;

public class DFSGraph {
    // Recursive function for DFS traversal
    private static void
    dfsRec(ArrayList<ArrayList<Integer> > adj,
           boolean[] visited, int s, ArrayList<Integer> res)
    {
        visited[s] = true;
        res.add(s);

        // Recursively visit all adjacent vertices that are
        // not visited yet
        for (int i : adj.get(s)) {
            if (!visited[i]) {
                dfsRec(adj, visited, i, res);
            }
        }
    }

    // Main DFS function that initializes the visited array
    // and calls dfsRec
    public static ArrayList<Integer>
    DFS(ArrayList<ArrayList<Integer> > adj)
    {
        boolean[] visited = new boolean[adj.size()];
        ArrayList<Integer> res = new ArrayList<>();
        dfsRec(adj, visited, 0, res);
        return res;
    }

    // To add an edge in an undirected graph
    public static void
    addEdge(ArrayList<ArrayList<Integer> > adj, int s,
            int t)
    {
        adj.get(s).add(t);
        adj.get(t).add(s);
    }

    public static void main(String[] args)
    {
        int V = 5;
        ArrayList<ArrayList<Integer> > adj
            = new ArrayList<>();

        // Initialize adjacency list
        for (int i = 0; i < V; i++) {
            adj.add(new ArrayList<>());
        }

        // Add edges
        int[][] edges= { { 1, 2 },{ 1, 0 },{ 2, 0 },{ 2, 3 },{ 2, 4 } }; 
        for (int[] e : edges)
        {
            addEdge(adj, e[0], e[1]);
        }

        // Perform DFS starting from vertex 0
        ArrayList<Integer> res = DFS(adj);

        for (int i = 0; i < res.size(); i++) {
            System.out.print(res.get(i) + " ");
        }
    }
}

				
					function dfsRec(adj, visited, s, res)
{
    visited[s] = true;
    res.push(s);

    // Recursively visit all adjacent vertices that are not
    // visited yet
    for (let i = 0; i < adj.length; i++) {
        if (adj[s][i] === 1 && !visited[i]) {
            dfsRec(adj, visited, i, res);
        }
    }
}

function DFS(adj)
{
    let visited = new Array(adj.length).fill(false);
    let res = [];
    dfsRec(adj, visited, 0, res); // Start DFS from vertex 0
    return res;
}

function addEdge(adj, s, t)
{
    adj[s][t] = 1;
    adj[t][s] = 1; // Since it's an undirected graph
}

// Driver code
let V = 5;
let adj = Array.from(
    {length : V},
    () => new Array(V).fill(0)); // Adjacency matrix

// Define the edges of the graph
let edges =
    [ [ 1, 2 ], [ 1, 0 ], [ 2, 0 ], [ 2, 3 ], [ 2, 4 ] ];

// Populate the adjacency matrix with edges
edges.forEach(([ s, t ]) => addEdge(adj, s, t));

let res = DFS(adj); // Perform DFS
console.log(res.join(" "));

				
					def dfsRec(adj, visited, s, res):
    visited[s] = True
    res.append(s)

    # Recursively visit all adjacent vertices that are not visited yet
    for i in range(len(adj)):
        if adj[s][i] == 1 and not visited[i]:
            dfsRec(adj, visited, i, res)


def DFS(adj):
    visited = [False] * len(adj)
    res = []
    dfsRec(adj, visited, 0, res)  # Start DFS from vertex 0
    return res


def add_edge(adj, s, t):
    adj[s][t] = 1
    adj[t][s] = 1  # Since it's an undirected graph


# Driver code
V = 5
adj = [[0] * V for _ in range(V)]  # Adjacency matrix

# Define the edges of the graph
edges = [(1, 2), (1, 0), (2, 0), (2, 3), (2, 4)]

# Populate the adjacency matrix with edges
for s, t in edges:
    add_edge(adj, s, t)

res = DFS(adj)  # Perform DFS
print(" ".join(map(str, res)))

Output

0 1 2 3 4

Time & Space Complexity:

Time: O(V + E)
Space: O(V + E) — for visited array and recursion stack

To sharpen your knowledge of similar algorithms, check out our DSA Crash Course.

DFS for Disconnected Undirected Graphs

If the graph is disconnected, DFS from one source won’t reach all nodes. In such cases, run DFS for each unvisited node.

				
					#include <bits/stdc++.h>
using namespace std;

void addEdge(vector<vector<int>> &adj, int s, int t)
{
    adj[s].push_back(t);
    adj[t].push_back(s);
}

// Recursive function for DFS traversal
void dfsRec(vector<vector<int>> &adj, vector<bool> &visited, int s, vector<int> &res)
{
    // Mark the current vertex as visited
    visited[s] = true;

    res.push_back(s);

    // Recursively visit all adjacent vertices that are not visited yet
    for (int i : adj[s])
        if (visited[i] == false)
            dfsRec(adj, visited, i, res);
}

// Main DFS function to perform DFS for the entire graph
vector<int> DFS(vector<vector<int>> &adj)
{
    vector<bool> visited(adj.size(), false);
    vector<int> res;
    // Loop through all vertices to handle disconnected graph
    for (int i = 0; i < adj.size(); i++)
    {
        if (visited[i] == false)
        {
            // If vertex i has not been visited,
            // perform DFS from it
            dfsRec(adj, visited, i, res);
        }
    }

    return res;
}

int main()
{
    int V = 6;
    // Create an adjacency list for the graph
    vector<vector<int>> adj(V);

    // Define the edges of the graph
    vector<vector<int>> edges = {{1, 2}, {2, 0}, {0, 3}, {4, 5}};

    // Populate the adjacency list with edges
    for (auto &e : edges)
        addEdge(adj, e[0], e[1]);
    vector<int> res = DFS(adj);

    for (auto it : res)
        cout << it << " ";
    return 0;
}

Searching

Traverse the loop to find a target value, requiring safeguards against infinite loops.

For a quick refresher on these operations, try our crash course.

Implementation of Circular Linked Lists

Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.

				
					import java.util.*;

public class GfG {
    // Function to add an edge to the adjacency list
    public static void
    addEdge(ArrayList<ArrayList<Integer> > adj, int s,
            int t)
    {
        adj.get(s).add(t);
        adj.get(t).add(s);
    }

    // Recursive function for DFS traversal
    private static void
    dfsRec(ArrayList<ArrayList<Integer> > adj,
           boolean[] visited, int s, ArrayList<Integer> res)
    {
        visited[s] = true;
        res.add(s);

        // Recursively visit all adjacent vertices that are
        // not visited yet
        for (int i : adj.get(s)) {
            if (!visited[i]) {
                dfsRec(adj, visited, i, res);
            }
        }
    }

    // Main DFS function to perform DFS for the entire graph
    public static ArrayList<Integer>
    DFS(ArrayList<ArrayList<Integer> > adj)
    {
        boolean[] visited = new boolean[adj.size()];
        ArrayList<Integer> res = new ArrayList<>();

        // Loop through all vertices to handle disconnected
        // graphs
        for (int i = 0; i < adj.size(); i++) {
            if (!visited[i]) {
                dfsRec(adj, visited, i, res);
            }
        }

        return res;
    }

    public static void main(String[] args)
    {
        int V = 6;
        // Create an adjacency list for the graph
        ArrayList<ArrayList<Integer> > adj
            = new ArrayList<>();

        // Initialize adjacency list
        for (int i = 0; i < V; i++) {
            adj.add(new ArrayList<>());
        }

        // Define the edges of the graph
        int[][] edges
            = { { 1, 2 }, { 2, 0 }, { 0, 3 }, { 4, 5 } };

        // Populate the adjacency list with edges
        for (int[] e : edges) {
            addEdge(adj, e[0], e[1]);
        }

        // Perform DFS
        ArrayList<Integer> res = DFS(adj);

        // Print the DFS traversal result
        for (int num : res) {
            System.out.print(num + " ");
        }
    }
}

				
					function addEdge(adj, s, t) {
    adj[s].push(t);
    adj[t].push(s);
}

// Recursive function for DFS traversal
function dfsRec(adj, visited, s, res) {
    visited[s] = true;
    res.push(s);

    // Recursively visit all adjacent vertices that are not visited yet
    for (let i of adj[s]) {
        if (!visited[i]) {
            dfsRec(adj, visited, i, res);
        }
    }
}

// Main DFS function to perform DFS for the entire graph
function DFS(adj) {
    let visited = new Array(adj.length).fill(false);
    let res = [];

    // Loop through all vertices to handle disconnected graphs
    for (let i = 0; i < adj.length; i++) {
        if (!visited[i]) {
            dfsRec(adj, visited, i, res);
        }
    }

    return res;
}

// Main Execution
let V = 6;
// Create an adjacency list for the graph
let adj = Array.from({ length: V }, () => []);

let edges = [[1, 2], [2, 0], [0, 3], [4, 5]];

// Populate the adjacency list with edges
for (let e of edges) {
    addEdge(adj, e[0], e[1]);
}

// Perform DFS
let res = DFS(adj);

// Print the DFS traversal result
console.log(res.join(" "));

Output Example:

0 2 1 3 4 5

Complexity:

Time: O(V + E)
Space: O(V + E)

Explore more real-world applications of DFS in our Web Development Course and Essential DSA + Web Dev Course.

Applications of DFS

Path Finding

Used in GPS navigation, maze solving, and AI for games.

Cycle Detection

Detecting cycles in both directed and undirected graphs.

Topological Sorting

Used in task scheduling and compiler design (for DAGs).

Connected Components

Identifying isolated groups of nodes in a graph.

You can practice advanced graph problems in our Master DSA + Web Dev + System Design Course.

Common DFS Interview Questions

Prepare for top tech interviews with handpicked DFS problems:

				
					# Create an adjacency list for the graph
from collections import defaultdict


def add_edge(adj, s, t):
    adj[s].append(t)
    adj[t].append(s)

# Recursive function for DFS traversal


def dfs_rec(adj, visited, s, res):
    # Mark the current vertex as visited
    visited[s] = True
    res.append(s)

    # Recursively visit all adjacent vertices that are not visited yet
    for i in adj[s]:
        if not visited[i]:
            dfs_rec(adj, visited, i, res)

# Main DFS function to perform DFS for the entire graph


def dfs(adj):
    visited = [False] * len(adj)
    res = []
    # Loop through all vertices to handle disconnected graph
    for i in range(len(adj)):
        if not visited[i]:
            # If vertex i has not been visited,
            # perform DFS from it
            dfs_rec(adj, visited, i, res)
    return res


V = 6
# Create an adjacency list for the graph
adj = defaultdict(list)

# Define the edges of the graph
edges = [[1, 2], [2, 0], [0, 3], [4, 5]]

# Populate the adjacency list with edges
for e in edges:
    add_edge(adj, e[0], e[1])
res = dfs(adj)

print(' '.join(map(str, res)))

What is the difference between DFS and BFS?

DFS goes as deep as possible in one direction before backtracking, while BFS explores level by level. If you want to learn both, check out our DSA Course.

Can DFS be used on directed graphs?

Yes, DFS works for both directed and undirected graphs. To explore more, consider our Web Development Course.

Is DFS recursive or iterative?

It can be implemented in both ways. The recursive version is simpler. Learn both techniques in our Design + DSA Combined Course.

When should I prefer DFS over BFS?

Use DFS for problems like topological sorting, solving puzzles, and detecting cycles. Master these use-cases in our Master DSA + Web Dev + System Design Course.

How is DFS used in real-world applications?

DFS is used in networking, pathfinding, scheduling tasks, and more. For data-focused applications, explore our Data Science Course.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Depth First Search (DFS) in Graphs: A Complete Guide

What is Depth First Search (DFS)?

How DFS Works: Core Concept

DFS Traversal Example (Using Insertion Order)

Example 1:

Expected Output:

Explanation:

Example 2:

Explanation:

DFS from a Given Source

Searching

Implementation of Circular Linked Lists

Output

Time & Space Complexity:

DFS for Disconnected Undirected Graphs

Searching

Implementation of Circular Linked Lists

Output Example:

Complexity:

Applications of DFS

Path Finding

Cycle Detection

Topological Sorting

Connected Components

Common DFS Interview Questions

What is the difference between DFS and BFS?

Can DFS be used on directed graphs?

Is DFS recursive or iterative?

When should I prefer DFS over BFS?

How is DFS used in real-world applications?

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Essentials of Machine Learning and Artificial Intelligence

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 57% OFF ₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Low & High Level System Design

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)

Buy for 60% OFF ₹15,000.00 ₹5,999.00

10 Day Google Interview Preparation Bootcamp

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 57% OFF
₹35,000.00 ₹14,999.00

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 60% OFF
₹15,000.00 ₹5,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design