Data Structures and Algorithms

DSA Interview Questions

Topological Sorting in Graphs: A Complete Guide for Developers and Data Scientists

Have you ever wondered how to sequence tasks that rely on one another, like putting on socks before shoes or compiling code with dependencies? Topological sorting provides the perfect solution! This powerful concept arranges the vertices of a Directed Acyclic Graph (DAG) in a linear order, ensuring that for every directed edge from vertex u to v, u comes before v. Whether you’re preparing for a tech interview or tackling real-world problems, understanding topological sorting is a must. Interested in mastering this and other key algorithms? Sign up for our free Data Structures and Algorithms course or fill out the form below to stay updated!

Note: Topological sorting is only possible in DAGs—graphs without cycles. Let’s dive into why that is and explore this topic in depth.

Example

Input:

				
					Vertices (V) = 6
Edges = [[2, 3], [3, 1], [4, 0], [4, 1], [5, 0], [5, 2]]

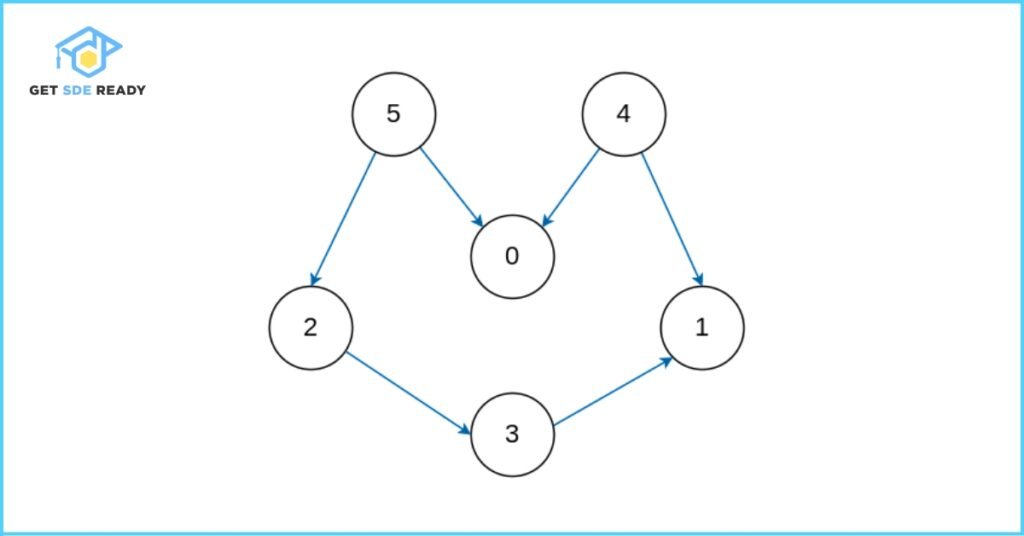
Output:

				
					5 4 2 3 1 0

Explanation:
In topological sorting, we start with vertices that have no incoming edges (in-degree of 0), like 5 and 4 in this graph. The sequence “5 4 2 3 1 0” satisfies the rule that for every edge u → v, u appears before v. Interestingly, this isn’t the only valid order—another possibility is “4 5 2 3 1 0”. This flexibility is a key feature of topological sorting.

Topological Sorting vs Depth First Traversal (DFS)

Topological sorting, however, is like creating a prioritized to-do list where each task depends on others being completed first. In DFS, we visit a vertex and then explore its neighbors recursively, printing as we go. In contrast, topological sorting ensures a vertex is printed before its neighbors, respecting dependencies.

For the graph above, a DFS starting at vertex 5 might yield “5 2 3 1 0 4″—a valid traversal but not a topological order, as 4 should precede 0 due to the edge 4 → 0. A correct topological sort, like “5 4 2 3 1 0”, aligns with the graph’s directed edges.

Curious about DFS? Check out our DSA course for a deeper dive.

Topological Sorting in Directed Acyclic Graphs (DAGs)

A Directed Acyclic Graph (DAG) is a directed graph with no cycles—think of it as a flowchart where tasks flow in one direction without looping back. Topological sorting thrives in DAGs because it relies on resolving dependencies linearly. But why is it exclusive to DAGs? Let’s break it down.

Why Topological Sort Fails in Undirected Graphs

In an undirected graph, edges go both ways: if u connects to v, v connects back to u. This mutual dependency creates an implicit cycle, making it impossible to place one vertex before the other without contradiction.

Why Cycles Break Topological Sort

Consider a cyclic graph with edges 1 → 2, 2 → 3, and 3 → 1. Start at 1, and you need 1 before 2, 2 before 3, but 3 before 1—an impossible loop! Cycles mean vertices depend on each other circularly, defying the linear order topological sorting demands.

Topological Order Isn’t Always Unique

Sure! Here’s the text exactly as you requested, without any changes:

What is Topological Sorting? (Minor heading for clarity)
Topological sorting solves dependency-based sequencing problems, where tasks must follow a specific order constrained by prerequisites. Imagine this real-world example:

Getting Dressed: A Topological Sorting Example
To reach school, you must first get dressed. Clothing choices follow dependencies—you can’t wear shoes before socks, for instance. The dependency graph below visualizes these rules.

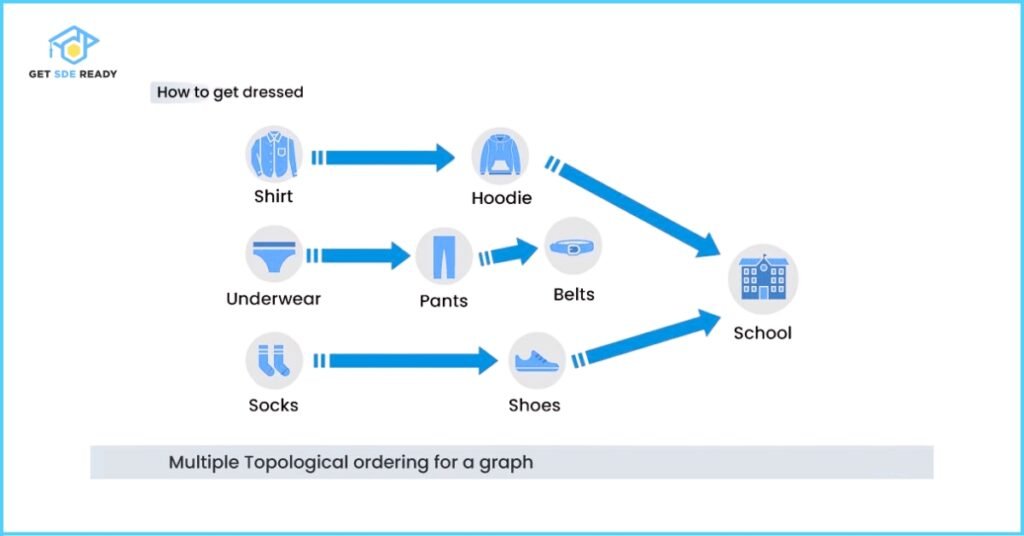
Multiple Valid Orderings Exist
As shown, there are numerous ways to order tasks while respecting dependencies. The image highlights a few valid sequences.

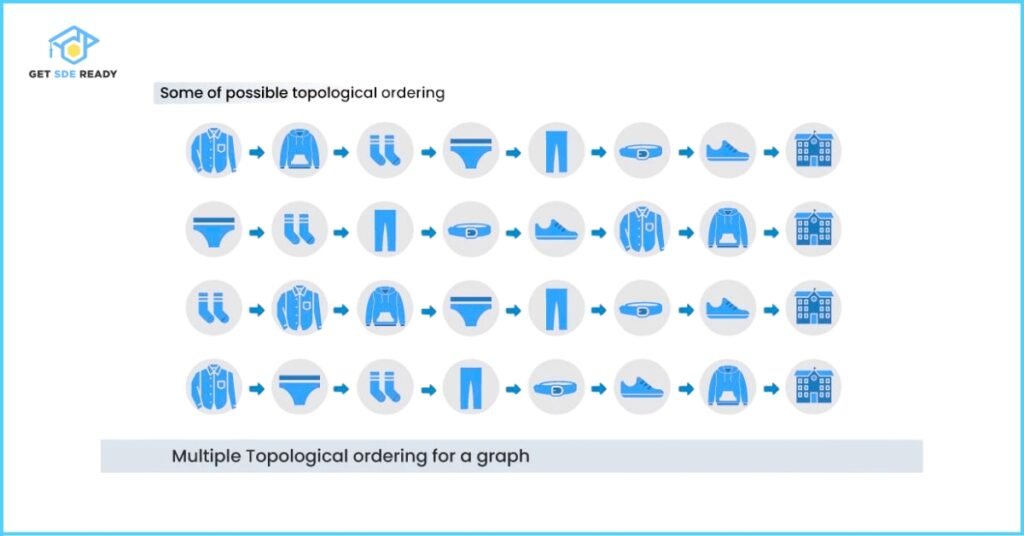
Challenge:
How many topological orderings can you derive from this clothing dependency graph? List all possible sequences to master this core graph algorithm concept!

Algorithm for Topological Sorting using DFS

Here’s how to perform topological sorting using DFS, step by step:

Build a graph with n vertices and m directed edges.
Set up a stack and a visited array of size n.
For each unvisited vertex:
- Run DFS: mark the vertex visited, explore all unvisited neighbors recursively, then push the vertex onto the stack once its neighbors are processed.
Pop the stack to get the topological order.

Example Walkthrough

Using the earlier graph (V = 6, edges = [[2, 3], [3, 1], [4, 0], [4, 1], [5, 0], [5, 2]]):

Start at 5: Visit 5 → 2 → 3 → 1 (push 1), back to 3 (push 3), back to 2 (push 2), 5 → 0 (push 0), push 5.
Move to 4: Visit 4, skip 0 and 1 (already visited), push 4.
Stack (top to bottom): 4, 5, 0, 2, 3, 1. Popping gives 5 4 2 3 1 0.

Time Complexity: O(V + E) — same as DFS, with an added stack.
Space Complexity: O(V) for the stack and visited array.

				
					#include <bits/stdc++.h>
using namespace std;

// Function to perform DFS and topological sorting
void topologicalSortUtil(int v, vector<vector<int>> &adj, vector<bool> &visited, stack<int> &st)
{

    // Mark the current node as visited
    visited[v] = true;

    // Recur for all adjacent vertices
    for (int i : adj[v])
    {
        if (!visited[i])
            topologicalSortUtil(i, adj, visited, st);
    }

    // Push current vertex to stack which stores the result
    st.push(v);
}

vector<vector<int>> constructadj(int V, vector<vector<int>> &edges)
{

    vector<vector<int>> adj(V);
    for (auto it : edges)
    {
        adj[it[0]].push_back(it[1]);
    }

    return adj;
}

// Function to perform Topological Sort
vector<int> topologicalSort(int V, vector<vector<int>> &edges)
{

    // Stack to store the result
    stack<int> st;

    vector<bool> visited(V, false);
    vector<vector<int>> adj = constructadj(V, edges);
    // Call the recursive helper function to store
    // Topological Sort starting from all vertices one by
    // one
    for (int i = 0; i < V; i++)
    {
        if (!visited[i])
            topologicalSortUtil(i, adj, visited, st);
    }

    vector<int> ans;

    // Append contents of stack
    while (!st.empty())
    {
        ans.push_back(st.top());
        st.pop();
    }

    return ans;
}

int main()
{

    // Graph represented as an adjacency list
    int v = 6;
    vector<vector<int>> edges = {{2, 3}, {3, 1}, {4, 0}, {4, 1}, {5, 0}, {5, 2}};

    vector<int> ans = topologicalSort(v, edges);

    for (auto node : ans)
    {
        cout << node << " ";
    }
    cout << endl;

    return 0;
}

Searching

Traverse the loop to find a target value, requiring safeguards against infinite loops.

For a quick refresher on these operations, try our crash course.

Implementation of Circular Linked Lists

Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.

				
					import java.util.*;

class GfG {

    private static void
    topologicalSortUtil(int v, List<Integer>[] adj,
                        boolean[] visited,
                        Stack<Integer> stack)
    {
        visited[v] = true;

        for (int i : adj[v]) {
            if (!visited[i]) {
                topologicalSortUtil(i, adj, visited, stack);
            }
        }

        stack.push(v);
    }
    static List<Integer>[] constructadj(int V,
                                        int[][] edges)
    {

        List<Integer>[] adj = new ArrayList[V];

        for (int i = 0; i < V; i++) {
            adj[i] = new ArrayList<>();
        }

        for (int[] edge : edges) {
            adj[edge[0]].add(edge[1]);
        }
        return adj;
    }
    static int[] topologicalSort(int V, int[][] edges)
    {
        Stack<Integer> stack = new Stack<>();
        boolean[] visited = new boolean[V];

        List<Integer>[] adj = constructadj(V, edges);
        for (int i = 0; i < V; i++) {
            if (!visited[i]) {
                topologicalSortUtil(i, adj, visited, stack);
            }
        }

        int[] result = new int[V];
        int index = 0;
        while (!stack.isEmpty()) {
            result[index++] = stack.pop();
        }

        return result;
    }

    public static void main(String[] args)
    {
        int v = 6;
        int[][] edges = {{2, 3}, {3, 1}, {4, 0},
                          {4, 1}, {5, 0}, {5, 2}};

        int[] ans = topologicalSort(v, edges);

        for (int node : ans) {
            System.out.print(node + " ");
        }
        System.out.println();
    }
}

				
					// Function to perform DFS and topological sorting
function topologicalSortUtil(v, adj, visited, st)
{
    // Mark the current node as visited
    visited[v] = true;

    // Recur for all adjacent vertices
    for (let i of adj[v]) {
        if (!visited[i])
            topologicalSortUtil(i, adj, visited, st);
    }

    // Push current vertex to stack which stores the result
    st.push(v);
}

function constructadj(V, edges)
{
    let adj = Array.from(
        {length : V},
        () => []); // Fixed the adjacency list declaration

    for (let it of edges) {
        adj[it[0]].push(
            it[1]); // Fixed adjacency list access
    }
    return adj;
}

// Function to perform Topological Sort
function topologicalSort(V, edges)
{
    // Stack to store the result
    let st = [];
    let visited = new Array(V).fill(false);

    let adj = constructadj(V, edges);

    // Call the recursive helper function to store
    // Topological Sort starting from all vertices one by
    // one
    for (let i = 0; i < V; i++) {
        if (!visited[i])
            topologicalSortUtil(i, adj, visited, st);
    }

    let ans = [];

    // Append contents of stack
    while (st.length > 0) {
        ans.push(st.pop());
    }

    return ans;
}

// Main function
let v = 6;
let edges = [
    [2, 3], [3, 1], [4, 0], [4, 1], [5, 0],
    [5, 2]
];

let ans = topologicalSort(v, edges);

console.log(ans.join(" ") + " ");

				
					# Function to perform DFS and topological sorting
def topologicalSortUtil(v, adj, visited, stack):
    # Mark the current node as visited
    visited[v] = True

    # Recur for all adjacent vertices
    for i in adj[v]:
        if not visited[i]:
            topologicalSortUtil(i, adj, visited, stack)

    # Push current vertex to stack which stores the result
    stack.append(v)


def constructadj(V, edges):
    adj = [[] for _ in range(V)]

    for it in edges:
        adj[it[0]].append(it[1])

    return adj

# Function to perform Topological Sort


def topologicalSort(V, edges):
    # Stack to store the result
    stack = []
    visited = [False] * V

    adj = constructadj(V, edges)
    # Call the recursive helper function to store
    # Topological Sort starting from all vertices one by one
    for i in range(V):
        if not visited[i]:
            topologicalSortUtil(i, adj, visited, stack)

    # Reverse stack to get the correct topological order
    return stack[::-1]


if __name__ == '__main__':
    # Graph represented as an adjacency list
    v = 6
    edges = [[2, 3], [3, 1], [4, 0], [4, 1], [5, 0], [5, 2]]

    ans = topologicalSort(v, edges)

    print(" ".join(map(str, ans)))

Topological Sorting Using BFS

Known as Kahn’s Algorithm, this BFS-based approach is intuitive and efficient:

Calculate the in-degree of each vertex (count of incoming edges).
Add all vertices with in-degree 0 to a queue.
While the queue isn’t empty:
- Remove a vertex, add it to the order.
- Reduce the in-degree of its neighbors by 1.
- Enqueue any neighbor whose in-degree drops to 0.
Verify all vertices are processed (if not, there’s a cycle).

Time Complexity: O(V + E).
Space Complexity: O(V) for the queue and in-degree array.

Advantages of Topological Sort

Simplifies scheduling tasks with dependencies.
Detects cycles in directed graphs.
Efficiently handles precedence-based problems.

Disadvantages of Topological Sort

Limited to DAGs—useless for cyclic or undirected graphs.
Multiple valid orders can complicate specific use cases.

Applications of Topological Sort

Scheduling tasks in project management or university courses.
Resolving dependencies in software builds (e.g., Makefile).
Managing package installations in systems like npm or apt.
Detecting deadlocks in operating systems.
Finding shortest paths in weighted DAGs (try our Data Science course for more!).
FAQs

What is topological sorting and why is it important?

Topological sorting is a linear ordering of vertices in a Directed Acyclic Graph (DAG) where, for every directed edge u → v, vertex u comes before v. It’s essential for tasks with dependencies, such as scheduling or resolving prerequisites in programming. To deepen your understanding of topological sorting and other key algorithms, explore our DSA Course.

How can I prepare for coding interviews?

Preparing for coding interviews requires mastering data structures, algorithms, and problem-solving techniques. You can ace your interviews with our comprehensive Master DSA, Web Dev, System Design Course, which covers all the essentials you need to succeed.

What skills do I need to become a web developer?

A: Becoming a web developer involves learning HTML, CSS, JavaScript, and popular frameworks like React or Angular. Kickstart your journey with our Web Development Course to build the skills employers demand.

Is it beneficial to learn both design and DSA?

A: Yes, combining design principles with data structures and algorithms (DSA) enhances both your creative and technical problem-solving abilities. Our Design and DSA Combined Course offers a perfect blend to strengthen these skills.

How can I transition into data science from a different field?

Transitioning to data science requires foundational knowledge in statistics, programming, and machine learning. Make the switch easier with our Data Science Course, tailored for career changers like you.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Topological Sorting in Graphs: A Complete Guide for Developers and Data Scientists

ExampleInput:

Output:

Topological Sorting vs Depth First Traversal (DFS)

Topological Sorting in Directed Acyclic Graphs (DAGs)

Why Topological Sort Fails in Undirected Graphs

Why Cycles Break Topological Sort

Topological Order Isn’t Always Unique

Algorithm for Topological Sorting using DFS

Example Walkthrough

Searching

Implementation of Circular Linked Lists

Topological Sorting Using BFS

Advantages of Topological Sort

Disadvantages of Topological Sort

Applications of Topological Sort

FAQs

What is topological sorting and why is it important?

How can I prepare for coding interviews?

What skills do I need to become a web developer?

Is it beneficial to learn both design and DSA?

How can I transition into data science from a different field?

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Low & High Level System Design

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Design Patterns Bootcamp

Buy for 50% OFF ₹2,000.00 ₹999.00

LLD Bootcamp

Buy for 50% OFF ₹2,000.00 ₹999.00

Essentials of Machine Learning and Artificial Intelligence

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 57% OFF ₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Example

Input:

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 50% OFF
₹2,000.00 ₹999.00

Buy for 50% OFF
₹2,000.00 ₹999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 57% OFF
₹35,000.00 ₹14,999.00

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design