Data Structures and Algorithms

DSA Interview Questions

How to Detect a Cycle in a Directed Graph

Detecting a cycle in a directed graph is a fundamental problem in graph theory and computer science. Given the number of vertices V and a list of directed edges, the task is to determine whether the graph contains any cycles.

Problem Statement

Input:

An integer V representing the number of vertices.
A list of directed edges edges[][], where each edge is represented as a pair [u, v] indicating a directed edge from vertex u to vertex v.

Output:

Return true if the directed graph contains a cycle.
Return false if no cycles are present in the graph.

Examples

Example 1:
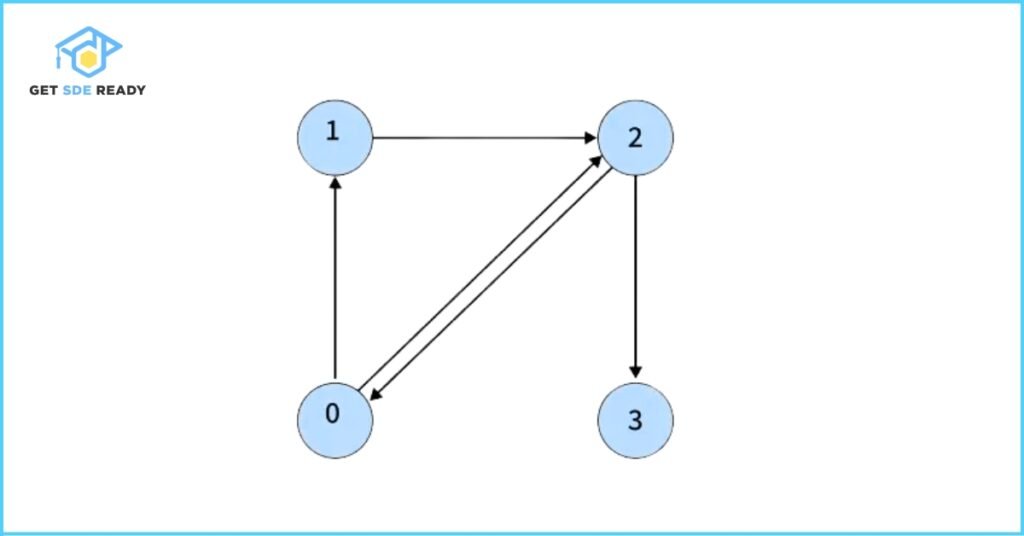
Input: V = 4, edges = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3]]
Output: true
Explanation: The graph contains a cycle: 0 → 2 → 0

Example 2:
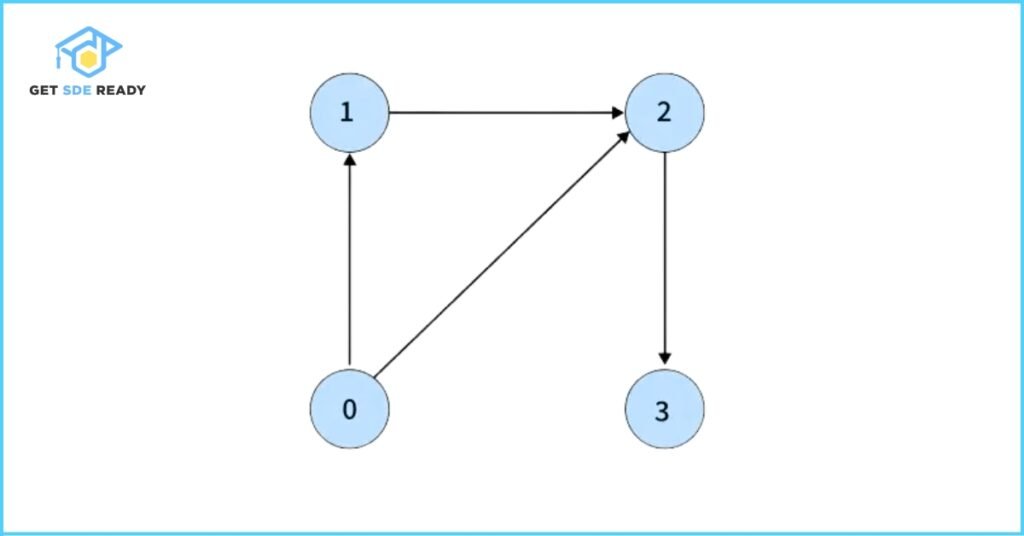
Input: V = 4, edges = [[0, 1], [0, 2], [1, 2], [2, 3]]
Output: false
Explanation: The graph has no cycles; all edges form a directed acyclic graph (DAG).

Approach 1 : Detect Cycle in a Directed Graph Using DFS

The cycle detection problem in a directed graph can be efficiently solved using Depth-First Search (DFS). This method relies on identifying back edges, which indicate the presence of a cycle.

Key Concept

In a directed graph, a cycle exists if there is a back edge—an edge that connects a vertex to one of its ancestors in the DFS traversal tree.

How DFS Helps Detect a Cycle

To detect a back edge using DFS, we need to:

Track all visited nodes.
Maintain a recursion stack to track nodes in the current DFS path.

During DFS traversal:

All ancestors of the current node are present in the recursion call stack.
If we find an edge from the current node to any node already in the stack, it means there is a back edge, hence a cycle.

Implementation Strategy

Use a boolean array visited[] to keep track of all visited vertices.
Use another boolean array recStack[] to track the recursion call stack:
- When a node’s DFS starts, mark it as true in recStack[].
- When DFS finishes for that node, mark it as false.
If during traversal we find an edge to a vertex that is already true in recStack[], it confirms the presence of a cycle.

Note:

If the directed graph is disconnected, it may consist of multiple components. In such cases, perform DFS on each disconnected component—this is known as constructing a DFS forest.

To detect a cycle in a disconnected graph:

Traverse each component individually using DFS.
Check for back edges in every DFS tree within the forest.

If any back edge is found in any component, the graph contains a cycle.

				
					#include <bits/stdc++.h>
using namespace std;

// Utility function for DFS to detect a cycle in a directed graph
bool isCyclicUtil(vector<vector<int>> &adj, int u, vector<bool> &visited, vector<bool> &recStack)
{
    // If the node is already in the recursion stack, a cycle is detected
    if (recStack[u])
        return true;

    // If the node is already visited and not in recursion stack, no need to check again
    if (visited[u])
        return false;

    // Mark the current node as visited and add it to the recursion stack
    visited[u] = true;
    recStack[u] = true;

    // Recur for all neighbors
    for (int x : adj[u])
    {
        if (isCyclicUtil(adj, x, visited, recStack))
            return true;
    }

    // Remove the node from the recursion stack
    recStack[u] = false;
    return false;
}

// Function to construct an adjacency list from edge list
vector<vector<int>> constructadj(int V, vector<vector<int>> &edges)
{
    vector<vector<int>> adj(V);
    for (auto &it : edges)
    {
        adj[it[0]].push_back(it[1]); // Directed edge from it[0] to it[1]
    }
    return adj;
}

// Function to detect cycle in a directed graph
bool isCyclic(int V, vector<vector<int>> &edges)
{
    // Construct the adjacency list
    vector<vector<int>> adj = constructadj(V, edges);

    // visited[] keeps track of visited nodes
    // recStack[] keeps track of nodes in the current recursion stack
    vector<bool> visited(V, false);
    vector<bool> recStack(V, false);

    // Check for cycles starting from every unvisited node
    for (int i = 0; i < V; i++)
    {
        if (!visited[i] && isCyclicUtil(adj, i, visited, recStack))
            return true; // Cycle found
    }

    return false; // No cycles detected
}

int main()
{
    int V = 4; // Number of vertices

    // Directed edges of the graph
    vector<vector<int>> edges = {{0, 1}, {0, 2}, {1, 2}, {2, 0}, {2, 3}};

    // Output whether the graph contains a cycle
    cout << (isCyclic(V, edges) ? "true" : "false") << endl;

    return 0;
}

				
					import java.util.*;

{

    // Function to perform DFS and detect cycle in a
    // directed graph
    private static boolean isCyclicUtil(List<Integer>[] adj,
                                        int u,
                                        boolean[] visited,
                                        boolean[] recStack)
    {
        // If the current node is already in the recursion
        // stack, a cycle is detected
        if (recStack[u])
            return true;

        // If already visited and not in recStack, it's not
        // part of a cycle
        if (visited[u])
            return false;

        // Mark the current node as visited and add it to
        // the recursion stack
        visited[u] = true;
        recStack[u] = true;

        // Recur for all adjacent vertices
        for (int v : adj[u]) {
            if (isCyclicUtil(adj, v, visited, recStack))
                return true;
        }

        // Backtrack: remove the vertex from recursion stack
        recStack[u] = false;
        return false;
    }

    // Function to construct adjacency list from edge list
    private static List<Integer>[] constructAdj(
        int V, int[][] edges)
    {
        // Create an array of lists
        List<Integer>[] adj = new ArrayList[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new ArrayList<>();
        }

        // Add edges to the adjacency list (directed)
        for (int[] edge : edges) {
            adj[edge[0]].add(edge[1]);
        }

        return adj;
    }

    // Main function to check if the directed graph contains
    // a cycle
    public static boolean isCyclic(int V, int[][] edges)
    {
        List<Integer>[] adj = constructAdj(V, edges);
        boolean[] visited = new boolean[V];
        boolean[] recStack = new boolean[V];

        // Perform DFS from each unvisited vertex
        for (int i = 0; i < V; i++) {
            if (!visited[i]
                && isCyclicUtil(adj, i, visited, recStack))
                return true; // Cycle found
        }

        return false; // No cycle found
    }

    public static void main(String[] args)
    {
        int V = 4; // Number of vertices

        // Directed edges of the graph
        int[][] edges = {
            { 0, 1 },
            { 0, 2 },
            { 1, 2 },
            { 2,
              0 }, // This edge creates a cycle (0 → 2 → 0)
            { 2, 3 }
        };

        // Print result
        System.out.println(isCyclic(V, edges) ? "true"
                                              : "false");
    }
}

				
					// Helper function to perform DFS and detect cycle
function isCyclicUtil(adj, u, visited, recStack)
{
    // If node is already in the recursion stack, cycle
    // detected
    if (recStack[u])
        return true;

    // If node is already visited and not in recStack, no
    // need to check again
    if (visited[u])
        return false;

    // Mark the node as visited and add it to the recursion
    // stack
    visited[u] = true;
    recStack[u] = true;

    // Recur for all neighbors of the current node
    for (let v of adj[u]) {
        if (isCyclicUtil(adj, v, visited, recStack))
            return true; // If any path leads to a cycle,
                         // return true
    }

    // Backtrack: remove the node from recursion stack
    recStack[u] = false;
    return false; // No cycle found in this path
}

// Function to construct adjacency list from edge list
function constructadj(V, edges)
{
    let adj = Array.from(
        {length : V},
        () => []); // Create an empty list for each vertex
    for (let [u, v] of edges) {
        adj[u].push(v); // Add directed edge from u to v
    }
    return adj;
}

// Main function to detect cycle in directed graph
function isCyclic(V, edges)
{
    let adj
        = constructadj(V, edges); // Build adjacency list
    let visited
        = new Array(V).fill(false); // Track visited nodes
    let recStack
        = new Array(V).fill(false); // Track recursion stack

    // Check each vertex (for disconnected components)
    for (let i = 0; i < V; i++) {
        if (!visited[i]
            && isCyclicUtil(adj, i, visited, recStack))
            return true; // Cycle found
    }

    return false; // No cycle detected
}

// Example usage
let V = 4;
let edges =
    [ [ 0, 1 ], [ 0, 2 ], [ 1, 2 ], [ 2, 0 ], [ 2, 3 ] ];

console.log(isCyclic(V, edges)); // Output: true

				
					# Helper function for DFS-based cycle detection
def isCyclicUtil(adj, u, visited, recStack):
    # If the node is already in the current recursion stack, a cycle is detected
    if recStack[u]:
        return True

    # If the node is already visited and not part of the recursion stack, skip it
    if visited[u]:
        return False

    # Mark the current node as visited and add it to the recursion stack
    visited[u] = True
    recStack[u] = True

    # Recur for all the adjacent vertices
    for v in adj[u]:
        if isCyclicUtil(adj, v, visited, recStack):
            return True

    # Remove the node from the recursion stack before returning
    recStack[u] = False
    return False

# Function to build adjacency list from edge list


def constructadj(V, edges):
    adj = [[] for _ in range(V)]  # Create a list for each vertex
    for u, v in edges:
        adj[u].append(v)  # Add directed edge from u to v
    return adj

# Main function to detect cycle in the directed graph


def isCyclic(V, edges):
    adj = constructadj(V, edges)
    visited = [False] * V       # To track visited vertices
    recStack = [False] * V      # To track vertices in the current DFS path

    # Try DFS from each vertex
    for i in range(V):
        if not visited[i] and isCyclicUtil(adj, i, visited, recStack):
            return True  # Cycle found
    return False  # No cycle found


# Example usage
V = 4  # Number of vertices
edges = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3]]

# Output: True, because there is a cycle (0 → 2 → 0)
print(isCyclic(V, edges))

Output:

true

Time Complexity:

O(V + E)
This is the same as the time complexity of a standard DFS traversal, where:

V is the number of vertices
E is the number of edges

Auxiliary Space Complexity:

O(V)
This accounts for:

The visited[] array
The recursion stack used during DFS

Note: The adjacency list is not counted as part of auxiliary space, as it is required to represent the input graph structure itself.

Approach 2 : Detect Cycle in a Directed Graph Using Topological Sorting

This approach leverages Kahn’s Algorithm for topological sorting to detect cycles in a directed graph.

Key Idea

Topological sorting is only possible in a Directed Acyclic Graph (DAG). If the graph contains a cycle, the algorithm will not be able to include all vertices in the topological order.

Cycle Detection Logic Using Kahn’s Algorithm

Compute the in-degree of all vertices.
Use a queue to store all vertices with in-degree 0.
Repeatedly remove vertices from the queue and reduce the in-degree of their adjacent nodes.
For every vertex removed, increase a count of processed vertices.

Conclusion:

If the number of processed vertices equals V (total number of vertices), the graph is a DAG (no cycles).
If there are any vertices left with non-zero in-degree, it means the graph contains at least one cycle.

Summary

Time Complexity: O(V + E)
Auxiliary Space: O(V) for in-degree array and queue

				
					#include <bits/stdc++.h>
using namespace std;

// Function to construct adjacency list from the given edges
vector<vector<int>> constructAdj(int V, vector<vector<int>> &edges)
{
    vector<vector<int>> adj(V);
    for (auto &edge : edges)
    {
        adj[edge[0]].push_back(edge[1]);
        // Directed edge from edge[0] to edge[1]
    }
    return adj;
}

// Function to check if a cycle exists in the directed graph using Kahn's Algorithm (BFS)
bool isCyclic(int V, vector<vector<int>> &edges)
{
    vector<vector<int>> adj = constructAdj(V, edges);
    // Build the adjacency list

    vector<int> inDegree(V, 0); // Array to store in-degree of each vertex
    queue<int> q;               // Queue to store nodes with in-degree 0
    int visited = 0;            // Count of visited (processed) nodes

    // Step 1: Compute in-degrees of all vertices
    for (int u = 0; u < V; ++u)
    {
        for (int v : adj[u])
        {
            inDegree[v]++;
        }
    }

    //  Add all vertices with in-degree 0 to the queue
    for (int u = 0; u < V; ++u)
    {
        if (inDegree[u] == 0)
        {
            q.push(u);
        }
    }

    // Perform BFS (Topological Sort)
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        visited++;

        // Reduce in-degree of neighbors
        for (int v : adj[u])
        {
            inDegree[v]--;
            if (inDegree[v] == 0)
            {
                // Add to queue when in-degree becomes 0
                q.push(v);
            }
        }
    }

    //  If visited nodes != total nodes, a cycle exists
    return visited != V;
}

int main()
{
    int V = 4; // Number of vertices
    vector<vector<int>> edges = {{0, 1}, {0, 2}, {1, 2}, {2, 0}, {2, 3}};

    // Output: true (cycle exists)
    cout << (isCyclic(V, edges) ? "true" : "false") << endl;

    return 0;
}

				
					import java.util.*;

{

    // Function to construct an adjacency list from edge
    // list
    static List<Integer>[] constructadj(int V,
                                        int[][] edges)
    {
        List<Integer>[] adj = new ArrayList[V];

        // Initialize each adjacency list
        for (int i = 0; i < V; i++) {
            adj[i] = new ArrayList<>();
        }

        // Add directed edges to the adjacency list
        for (int[] edge : edges) {
            adj[edge[0]].add(edge[1]); // Directed edge from
                                       // edge[0] to edge[1]
        }

        return adj;
    }

    // Function to check if the directed graph contains a
    // cycle using Kahn's Algorithm
    static boolean isCyclic(int V, int[][] edges)
    {
        List<Integer>[] adj
            = constructadj(V, edges); //  Build graph

        int[] inDegree
            = new int[V]; // Array to store in-degree of
                          // each vertex
        Queue<Integer> q
            = new LinkedList<>(); // Queue for BFS
        int visited
            = 0; // Count of visited (processed) nodes

        //  Compute in-degrees of all vertices
        for (int u = 0; u < V; u++) {
            for (int v : adj[u]) {
                inDegree[v]++;
            }
        }

        //  Enqueue all nodes with in-degree 0
        for (int u = 0; u < V; u++) {
            if (inDegree[u] == 0) {
                q.offer(u);
            }
        }

        // Perform BFS (Topological Sort)
        while (!q.isEmpty()) {
            int u = q.poll();
            visited++;

            // Reduce in-degree of all adjacent vertices
            for (int v : adj[u]) {
                inDegree[v]--;
                if (inDegree[v] == 0) {
                    q.offer(v);
                }
            }
        }

        //  If not all vertices were visited, there's a
        //  cycle
        return visited != V;
    }

    public static void main(String[] args)
    {
        int V = 4; // Number of vertices
        int[][] edges = {
            { 0, 1 }, { 0, 2 }, { 1, 2 }, { 2, 0 }, { 2, 3 }
        };

        // Output: true (cycle detected)
        System.out.println(isCyclic(V, edges) ? "true"
                                              : "false");
    }
}

				
					// Function to construct the adjacency list from edge list
function constructadj(V, edges)
{
    // Initialize an adjacency list with V empty arrays
    let adj = Array.from({length : V}, () => []);

    // Populate the adjacency list (directed edge u → v)
    for (let [u, v] of edges) {
        adj[u].push(v);
    }

    return adj;
}

// Function to detect a cycle in a directed graph using
// Kahn's Algorithm
function isCyclic(V, edges)
{
    let adj = constructadj(V, edges);
    let inDegree = new Array(V).fill(0);
    let queue = [];
    let visited = 0;

    for (let u = 0; u < V; u++) {
        for (let v of adj[u]) {
            inDegree[v]++;
        }
    }
    // Enqueue all nodes with in-degree 0
    for (let u = 0; u < V; u++) {
        if (inDegree[u] === 0) {
            queue.push(u);
        }
    }

    //  Process nodes with in-degree 0
    while (queue.length > 0) {
        let u = queue.shift(); // Dequeue
        visited++; // Mark node as visited

        // Reduce in-degree of adjacent nodes
        for (let v of adj[u]) {
            inDegree[v]--;
            if (inDegree[v] === 0) {
                queue.push(
                    v); // Enqueue if in-degree becomes 0
            }
        }
    }

    //  If not all nodes were visited, there's a cycle
    return visited !== V;
}

// Example usage
const V = 4;
const edges =
    [ [ 0, 1 ], [ 0, 2 ], [ 1, 2 ], [ 2, 0 ], [ 2, 3 ] ];

// Output: true (cycle exists: 0 → 2 → 0)
console.log(isCyclic(V, edges) ? "true" : "false");

				
					# Function to construct adjacency list from edge list


def constructadj(V, edges):
    adj = [[] for _ in range(V)]  # Initialize empty list for each vertex
    for u, v in edges:
        adj[u].append(v)          # Directed edge from u to v
    return adj

# Function to check for cycle using Kahn's Algorithm (BFS-based Topological Sort)


def isCyclic(V, edges):
    adj = constructadj(V, edges)
    in_degree = [0] * V
    queue = deque()
    visited = 0                       # Count of visited nodes

    #  Calculate in-degree of each node
    for u in range(V):
        for v in adj[u]:
            in_degree[v] += 1

    #  Enqueue nodes with in-degree 0
    for u in range(V):
        if in_degree[u] == 0:
            queue.append(u)

    #  Perform BFS (Topological Sort)
    while queue:
        u = queue.popleft()
        visited += 1

        # Decrease in-degree of adjacent nodes
        for v in adj[u]:
            in_degree[v] -= 1
            if in_degree[v] == 0:
                queue.append(v)

    #  If visited != V, graph has a cycle
    return visited != V


# Example usage
V = 4
edges = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3]]

# Output: true (because there is a cycle: 0 → 2 → 0)
print("true" if isCyclic(V, edges) else "false")

Output:

true

Time Complexity:

O(V + E)
The time complexity is equivalent to the time complexity of Breadth-First Search (BFS) traversal, where:

V is the number of vertices
E is the number of edges

Auxiliary Space Complexity:

O(V)
This includes:

The queue used for processing vertices
The in-degree array used to track incoming edges

Note: The adjacency list is not considered part of the auxiliary space, as it is essential for representing the input graph structure.

Network Routing in Computer Networking

The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.

Flight Connectivity in Aviation

In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.

Geographic Information Systems (GIS)

GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.

Kleene’s Algorithm and Formal Language Theory

A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.

Output:

true

Time Complexity:

O(V + E)
This is the same as the time complexity of a standard DFS traversal, where:

V is the number of vertices
E is the number of edges

Auxiliary Space Complexity:

O(V)
This accounts for:

The visited[] array
The recursion stack used during DFS

Note: The adjacency list is not counted as part of auxiliary space, as it is required to represent the input graph structure itself.

Approach 2 : Detect Cycle in a Directed Graph Using Topological Sorting

This approach leverages Kahn’s Algorithm for topological sorting to detect cycles in a directed graph.

Key Idea

Topological sorting is only possible in a Directed Acyclic Graph (DAG). If the graph contains a cycle, the algorithm will not be able to include all vertices in the topological order.

Cycle Detection Logic Using Kahn’s Algorithm

Compute the in-degree of all vertices.
Use a queue to store all vertices with in-degree 0.
Repeatedly remove vertices from the queue and reduce the in-degree of their adjacent nodes.
For every vertex removed, increase a count of processed vertices.

Conclusion:

If the number of processed vertices equals V (total number of vertices), the graph is a DAG (no cycles).
If there are any vertices left with non-zero in-degree, it means the graph contains at least one cycle.

Summary

Time Complexity: O(V + E)
Auxiliary Space: O(V) for in-degree array and queue

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

How to Detect a Cycle in a Directed Graph

Problem Statement

Examples

Approach 1 : Detect Cycle in a Directed Graph Using DFS

Key Concept

How DFS Helps Detect a Cycle

Implementation Strategy

Note:

Output:

Time Complexity:

Auxiliary Space Complexity:

Approach 2 : Detect Cycle in a Directed Graph Using Topological Sorting

Key Idea

Cycle Detection Logic Using Kahn’s Algorithm

Summary

Output:

Time Complexity:

Auxiliary Space Complexity:

Network Routing in Computer Networking

Flight Connectivity in Aviation

Geographic Information Systems (GIS)

Kleene’s Algorithm and Formal Language Theory

Output:

Time Complexity:

Auxiliary Space Complexity:

Approach 2 : Detect Cycle in a Directed Graph Using Topological Sorting

Key Idea

Cycle Detection Logic Using Kahn’s Algorithm

Conclusion:

Summary

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Essentials of Machine Learning and Artificial Intelligence

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 57% OFF ₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Low & High Level System Design

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)

Buy for 60% OFF ₹15,000.00 ₹5,999.00

10 Day Google Interview Preparation Bootcamp

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 57% OFF
₹35,000.00 ₹14,999.00

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 60% OFF
₹15,000.00 ₹5,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design