Data Structures and Algorithms

DSA Interview Questions

Trie Data Structure Trie Data Structure: Basics and Applications

The Trie data structure, also known as a prefix tree, is a specialized tree-based structure designed for efficiently storing and retrieving strings from a dynamic dataset. It excels in scenarios involving large volumes of words or keys, making it a powerful tool for applications like autocomplete and spell checking.

Key Features and Operations

Trie enables fast operations such as insertion, search, deletion, and prefix matching, significantly reducing time complexity when compared to traditional search techniques. This makes it ideal for tasks where performance and accuracy in string handling are crucial.

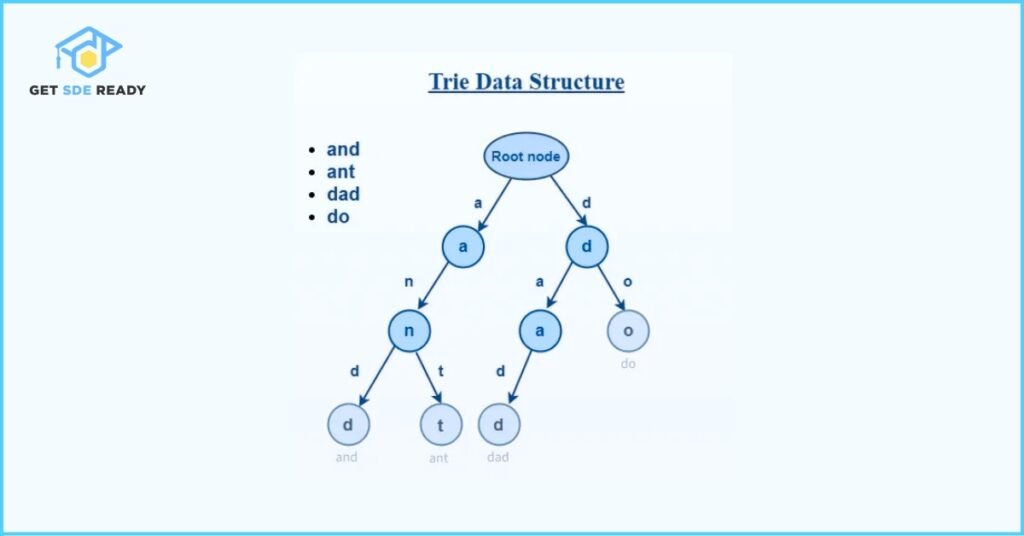
In this article, we’ll dive into how Tries manage operations like inserting and searching keys, as well as performing efficient prefix-based lookups.

Representation of Trie Node

Structure of a Trie Node

A Trie node serves as a fundamental unit in the Trie data structure, connected to other nodes through edges.
Each node typically holds a character or a segment of a string, forming a hierarchical structure.

The root node of the Trie functions as the starting point and is unique in that it does not store any character. It merely acts as an anchor to initiate traversal through the tree.

				
					class TrieNode {
public:

    // pointer array for child nodes of each node
    TrieNode* children[26];

    // Used for indicating ending of string
    bool isLeaf;

    TrieNode() {
      
        // initialize the wordEnd variable with false
        // initialize every index of childNode array with NULL
        isLeaf = false;
        for (int i = 0; i < 26; i++) {
            children[i] = nullptr;
        }
    }
};

				
					public class TrieNode {
    
    // Array for child nodes of each node
    TrieNode[] children;
    
    // Used for indicating the end of a string
    boolean isEndOfWord;

    // Constructor
    public TrieNode() {
      
        // Initialize the wordEnd 
        // variable with false
        isEndOfWord = false;

        // Initialize every index of 
        // the child array with null
        // In Java, we do not have to 
        // explicitely assign null as 
        // the values are by default 
        // assigned as null 
        children = new TrieNode[26];
    }
}

				
					class TrieNode {
    constructor() {
    
        // Initialize the child Node
        // array with 26 nulls
        this.children = Array(26).fill(null);
        
        // Initialize wordEnd to the false
        // indicating that no word ends here yet
        this.isEndOfWord = false;
    }
}

				
					class TrieNode:
    def __init__(self):
        self.children = [None] * 26
        self.isEndOfWord = False

Output

If a valid color configuration is found, the output will display the assigned colors for each vertex:

Solution Exists: Following are the assigned colors

1 2 3 2

Applications of Graph Coloring

Graph coloring has a wide range of real-world applications, particularly in areas where resource allocation or conflict resolution is required. Common use cases include:

Timetable Scheduling – Assigning time slots to avoid clashes in exams or classes.
Sudoku Solver – Treating each cell as a vertex and ensuring numbers don’t repeat in rows, columns, or blocks.
Register Allocation in Compilers – Optimizing the use of limited CPU registers during program execution.
Map Coloring – Ensuring neighboring regions or countries are colored differently on a map.
Mobile Radio Frequency Assignment – Assigning frequencies to avoid interference between adjacent towers.

FAQs

Insertion in Trie Data Structure – O(n) Time | O(n) Space

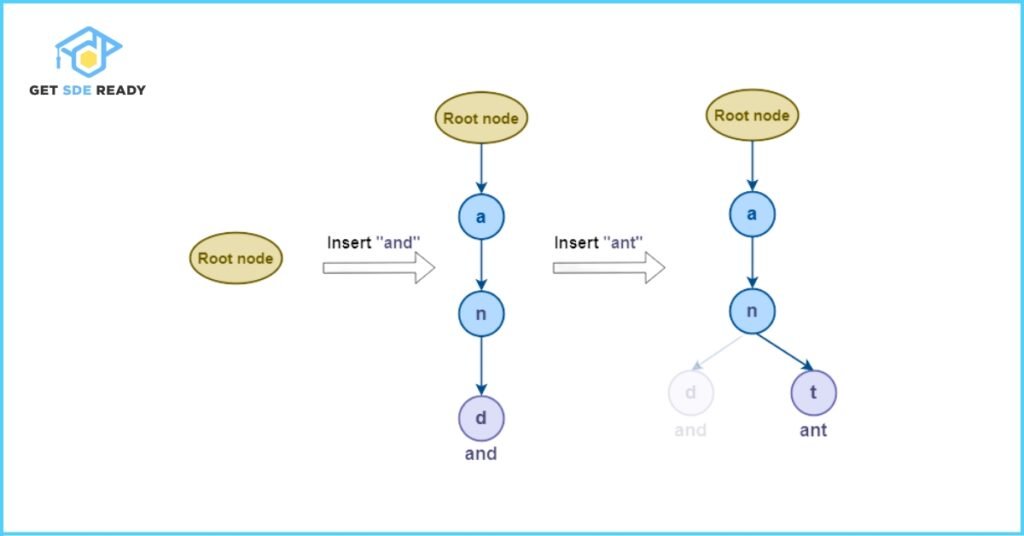
Example: Inserting the Word “and”

Start at the root node:
The root node does not contain any character. Its wordEnd value is set to 0, indicating that no word ends at this point.
First character – “a”:
Calculate the index: ‘a’ – ‘a’ = 0.
Check if child[0] is null. Since it is, create a new TrieNode for the character “a” with wordEnd = 0 and an empty array of children. Move to this newly created node.
Second character – “n”:
Calculate the index: ‘n’ – ‘a’ = 13.
Check if child[13] is null. It is, so create a new TrieNode for “n” with wordEnd = 0. Move to this node.
Third character – “d”:
Calculate the index: ‘d’ – ‘a’ = 3.
Since child[3] is null, create a new TrieNode for “d” and set wordEnd = 1, marking the end of the word “and”.

Example: Inserting the Word “ant”

Start at the root node:
The root node remains unchanged and keeps track of the starting characters of all inserted strings.
First character – “a”:
Index: ‘a’ – ‘a’ = 0.
A node for “a” already exists from the previous insertion. Move to this existing node.
Second character – “n”:
Index: ‘n’ – ‘a’ = 13.
The node for “n” is also present. Proceed to this node.
Third character – “t”:
Index: ‘t’ – ‘a’ = 19.
Since child[19] is null, create a new TrieNode for “t” and set wordEnd = 1, indicating that the word “ant” ends here.

				
					// Method to insert a key into the Trie
void insert(TrieNode* root, const string& key) {
  
    // Initialize the curr pointer with the root node
    TrieNode* curr = root;

    // Iterate across the length of the string
    for (char c : key) {
      
        // Check if the node exists for the 
        // current character in the Trie
        if (curr->children[c - 'a'] == nullptr) {
          
            // If node for current character does 
            // not exist then make a new node
            TrieNode* newNode = new TrieNode();
          
            // Keep the reference for the newly
            // created node
            curr->children[c - 'a'] = newNode;
        }
      
        // Move the curr pointer to the
        // newly created node
        curr = curr->children[c - 'a'];
    }

    // Mark the end of the word
    curr->isLeaf = true;
}

				
					// Method to insert a key into the Trie
static void insert(TrieNode root, String key) {

    // Initialize the curr pointer with the root node
    TrieNode curr = root;

    // Iterate across the length of the string
    for (char c : key.toCharArray()) {

        // Check if the node exists for the
        // current character in the Trie
        if (curr.children[c - 'a'] == null) {

            // If node for current character does
            // not exist then make a new node
            TrieNode newNode = new TrieNode();

            // Keep the reference for the newly
            // created node
            curr.children[c - 'a'] = newNode;
        }

        // Move the curr pointer to the
        // newly created node
        curr = curr.children[c - 'a'];
    }

    // Mark the end of the word
    curr.isEndOfWord = true;
}

				
					// Method to insert a key into the Trie
function insert(root, key) {

    // Initialize the curr pointer with the root node
    let curr = root;

    // Iterate across the length of the string
    for (let c of key) {

        // Check if the node exists for the 
        // current character in the Trie
        let index = c.charCodeAt(0) - 'a'.charCodeAt(0);
        if (curr.children[index] === null) {

            // If node for current character does 
            // not exist then make a new node
            let newNode = new TrieNode();

            // Keep the reference for the newly
            // created node
            curr.children[index] = newNode;
        }

        // Move the curr pointer to the
        // newly created node
        curr = curr.children[index];
    }

    // Mark the end of the word
    curr.isEndOfWord = true;
}

Time and Space Complexity of Insertion

Time Complexity:
O(n) — where n is the length of the word being inserted. This is because each character of the word is processed exactly once during insertion.
Auxiliary Space:
O(n) — in the worst-case scenario, a new node is created for each character if none of the characters are already present in the Trie.

Searching in Trie Data Structure

Time Complexity: O(n)

Auxiliary Space: O(1)

Searching in a Trie is similar to the insertion operation but without creating new nodes. The algorithm simply navigates through existing paths by comparing each character of the input string.

The search process may terminate in two cases:

When the end of the string is reached.
When a required character node is not found in the Trie.

Example: Searching for the Word “dad”

Assume the Trie already contains the words: “and”, “ant”, and “dad”. Now, let’s walk through the steps to search for the word “dad”:

Start at the root node.
Check for the character ‘d’: Navigate to the corresponding child node.
Next, check for the character ‘a’: Move to the child node linked to ‘a’.
Then, check for the character ‘d’ again: Move to the final character’s node.
Verify the wordEnd flag: If it is set to 1, this confirms that the word “dad” exists in the Trie.

If all characters are found and the final node marks the end of a word, the search is successful.

				
					# Method to insert a key into the Trie
def insert(root, key):

    # Initialize the curr pointer with the root node
    curr = root

    # Iterate across the length of the string
    for c in key:

        # Check if the node exists for the
        # current character in the Trie
        index = ord(c) - ord('a')
        if curr.children[index] is None:

            # If node for current character does
            # not exist then make a new node
            new_node = TrieNode()

            # Keep the reference for the newly
            # created node
            curr.children[index] = new_node

        # Move the curr pointer to the
        # newly created node
        curr = curr.children[index]

    # Mark the end of the word
    curr.isEndOfWord = True

Output

If a valid color configuration is found, the output will display the assigned colors for each vertex:

Solution Exists: Following are the assigned colors

1 2 3 2

Applications of Graph Coloring

Graph coloring has a wide range of real-world applications, particularly in areas where resource allocation or conflict resolution is required. Common use cases include:

Timetable Scheduling – Assigning time slots to avoid clashes in exams or classes.
Sudoku Solver – Treating each cell as a vertex and ensuring numbers don’t repeat in rows, columns, or blocks.
Register Allocation in Compilers – Optimizing the use of limited CPU registers during program execution.
Map Coloring – Ensuring neighboring regions or countries are colored differently on a map.
Mobile Radio Frequency Assignment – Assigning frequencies to avoid interference between adjacent towers.

FAQs

What is graph coloring?

Graph coloring is the process of assigning colors to each vertex of a graph such that no two adjacent vertices have the same color.

What is the chromatic number of a graph?

The chromatic number is the smallest number of colors needed to color a graph without any two connected vertices sharing the same color.

Why is graph coloring considered NP-complete?

Because there’s no known efficient algorithm that solves all instances of the problem in polynomial time. Finding an optimal coloring is computationally hard.

What is the difference between the decision and optimization versions of graph coloring?

The decision version asks whether a graph can be colored with M colors. The optimization version tries to find the minimum number of colors required to color the graph.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Trie Data Structure Trie Data Structure: Basics and Applications

Key Features and Operations

Representation of Trie Node

Structure of a Trie Node

Output

Applications of Graph Coloring

FAQs

Insertion in Trie Data Structure – O(n) Time | O(n) Space

Example: Inserting the Word “and”

Example: Inserting the Word “ant”

Time and Space Complexity of Insertion

Searching in Trie Data Structure

Time Complexity: O(n)

Auxiliary Space: O(1)

Example: Searching for the Word “dad”

Output

Applications of Graph Coloring

FAQs

What is graph coloring?

What is the chromatic number of a graph?

Why is graph coloring considered NP-complete?

What is the difference between the decision and optimization versions of graph coloring?

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Essentials of Machine Learning and Artificial Intelligence

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 57% OFF ₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Low & High Level System Design

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)

Buy for 60% OFF ₹15,000.00 ₹5,999.00

10 Day Google Interview Preparation Bootcamp

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 57% OFF
₹35,000.00 ₹14,999.00

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 60% OFF
₹15,000.00 ₹5,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design