Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Mastering Binary Heaps: A Deep Dive into Min and Max Heaps
Imagine a bustling airport where flights are prioritized based on urgency—emergencies take off first, while routine flights wait their turn. This efficient prioritization is powered by a fascinating data structure called the Binary Heap. Whether you’re gearing up for a coding interview or aiming to level up your algorithmic skills, mastering Binary Heaps is a game-changer. In this detailed guide, we’ll unravel the magic of Min and Max Heaps, their operations, and real-world applications. Want to supercharge your learning? Sign up for our free mini-course on data structures and get the latest updates delivered straight to your inbox—click here to join!

What Are Binary Heaps?
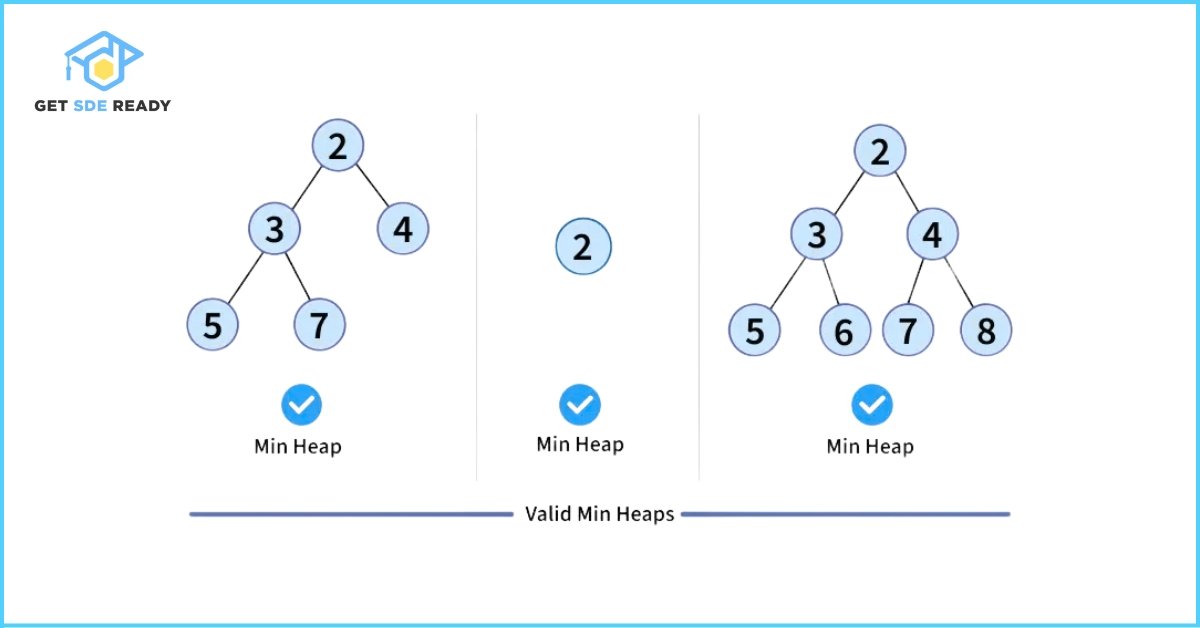
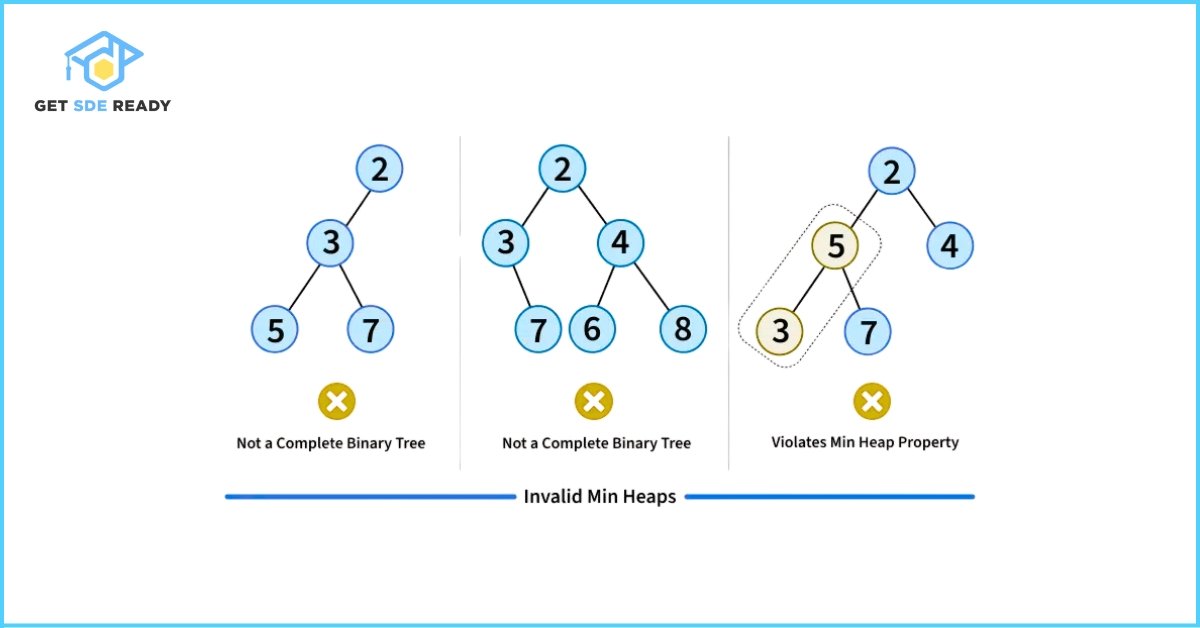
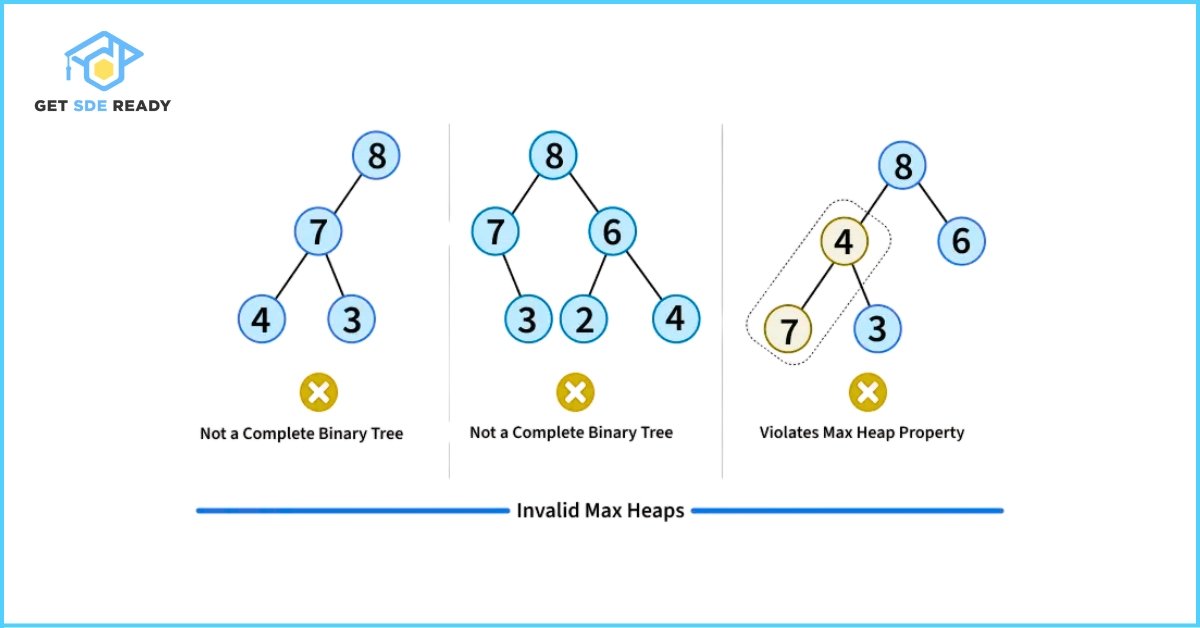
A Binary Heap is a specialized complete binary tree designed for rapid access to the smallest or largest element. “Complete” means all levels are fully filled except possibly the last, which is packed from left to right. The defining trait of a heap—the heap property—determines its type:
- Min Heap: Every node’s value is greater than or equal to its parent’s, placing the smallest element at the root.
- Max Heap: Every node’s value is less than or equal to its parent’s, ensuring the largest element sits at the root.
Think of it as a leaderboard: a Min Heap crowns the underdog, while a Max Heap celebrates the champion.
Valid and Invalid examples of heaps

How Binary Heaps Are Represented
Thanks to their complete structure, Binary Heaps are elegantly stored as arrays—no pointers needed. This compact representation boosts efficiency. For any element at index i in the array:
- Parent: Found at floor((i-1)/2)
- Left Child: Located at 2*i + 1
- Right Child: Positioned at 2*i + 2
For instance, a Min Heap array [4, 10, 15, 20, 25] has 4 as the root, with 10 and 15 as its children. This array-based approach simplifies navigation and speeds up operations.
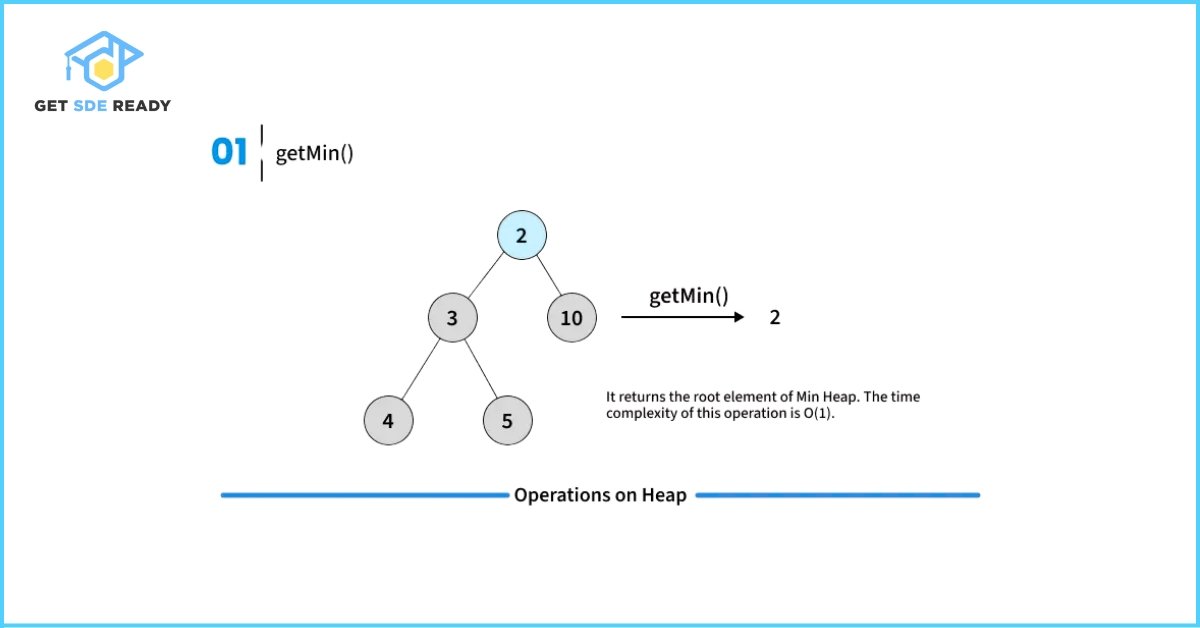
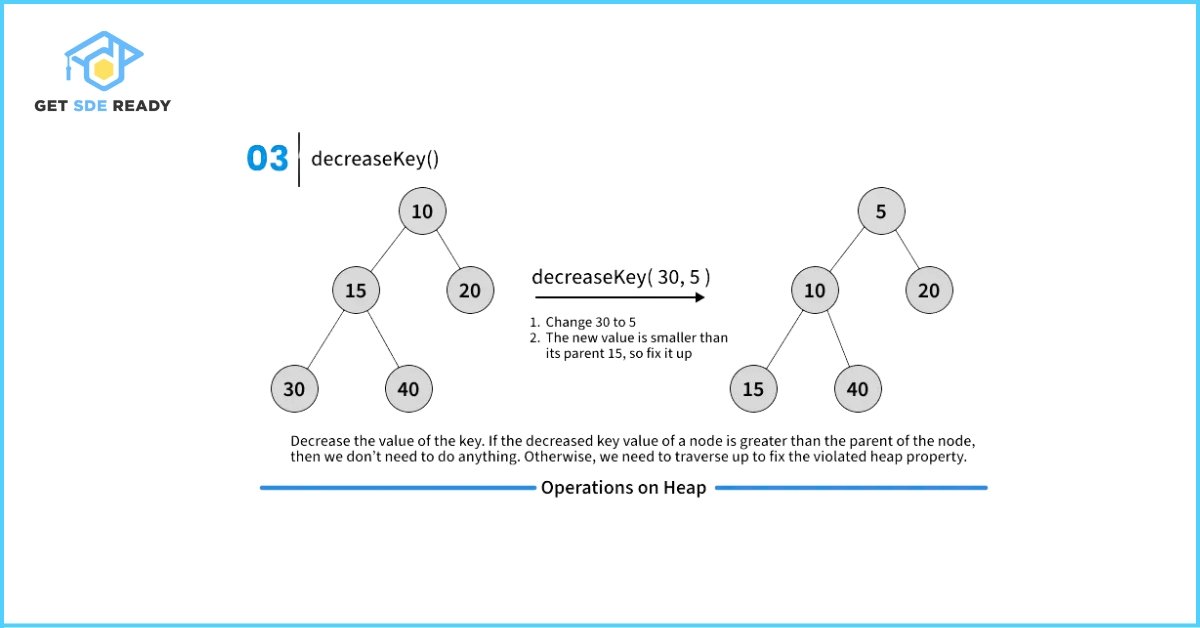
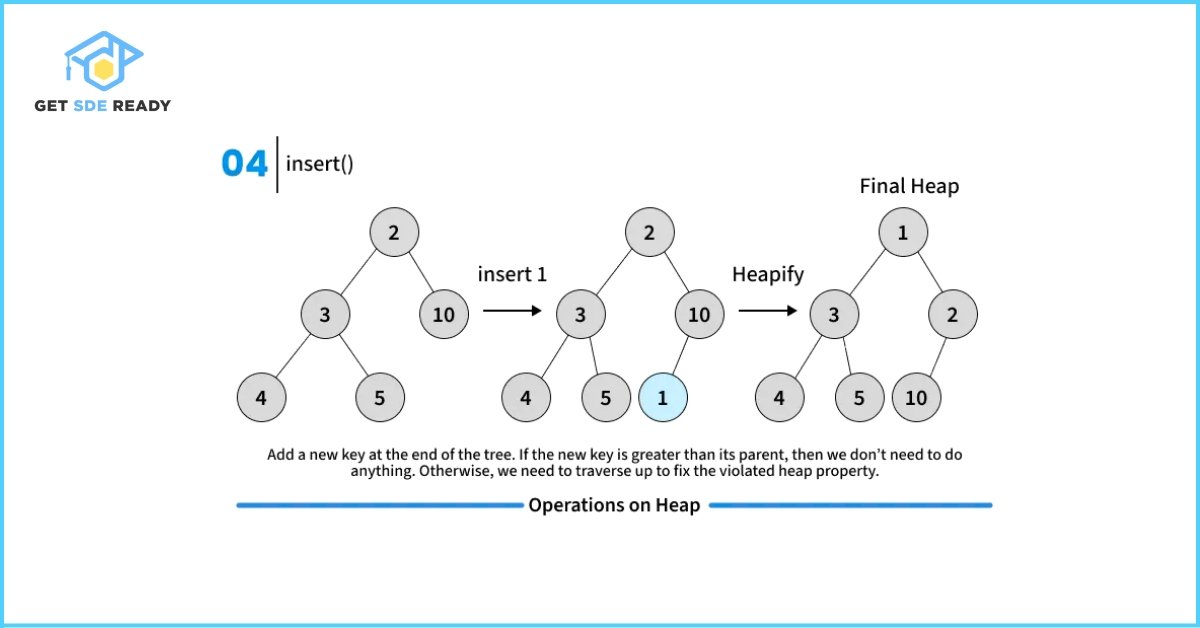
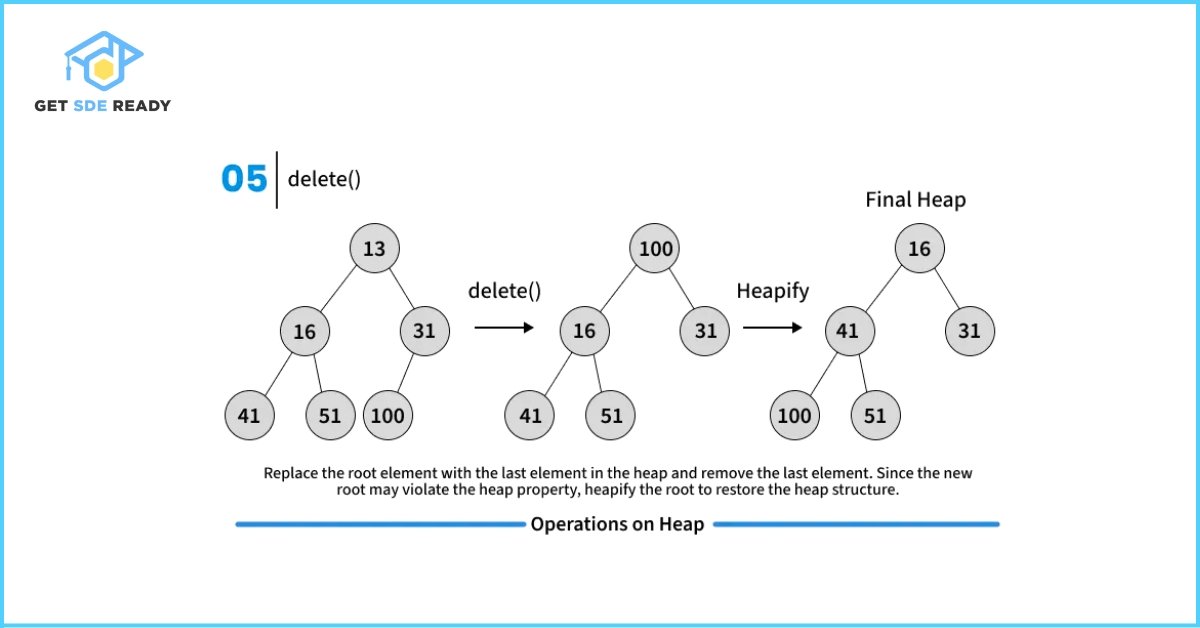
Key Operations on Binary Heaps

// A C++ program to demonstrate common Binary Heap Operations
#include<iostream>
#include<climits>
using namespace std;
// Prototype of a utility function to swap two integers
void swap(int *x, int *y);
// A class for Min Heap
class MinHeap
{
int *harr; // pointer to array of elements in heap
int capacity; // maximum possible size of min heap
int heap_size; // Current number of elements in min heap
public:
// Constructor
MinHeap(int capacity);
// to heapify a subtree with the root at given index
void MinHeapify(int i);
int parent(int i) { return (i-1)/2; }
// to get index of left child of node at index i
int left(int i) { return (2*i + 1); }
// to get index of right child of node at index i
int right(int i) { return (2*i + 2); }
// to extract the root which is the minimum element
int extractMin();
// Decreases key value of key at index i to new_val
void decreaseKey(int i, int new_val);
// Returns the minimum key (key at root) from min heap
int getMin() { return harr[0]; }
// Deletes a key stored at index i
void deleteKey(int i);
// Inserts a new key 'k'
void insertKey(int k);
};
// Constructor: Builds a heap from a given array a[] of given size
MinHeap::MinHeap(int cap)
{
heap_size = 0;
capacity = cap;
harr = new int[cap];
}
// Inserts a new key 'k'
void MinHeap::insertKey(int k)
{
if (heap_size == capacity)
{
cout << "\nOverflow: Could not insertKey\n";
return;
}
// First insert the new key at the end
heap_size++;
int i = heap_size - 1;
harr[i] = k;
// Fix the min heap property if it is violated
while (i != 0 && harr[parent(i)] > harr[i])
{
swap(&harr[i], &harr[parent(i)]);
i = parent(i);
}
}
// Decreases value of key at index 'i' to new_val. It is assumed that
// new_val is smaller than harr[i].
void MinHeap::decreaseKey(int i, int new_val)
{
harr[i] = new_val;
while (i != 0 && harr[parent(i)] > harr[i])
{
swap(&harr[i], &harr[parent(i)]);
i = parent(i);
}
}
// Method to remove minimum element (or root) from min heap
int MinHeap::extractMin()
{
if (heap_size <= 0)
return INT_MAX;
if (heap_size == 1)
{
heap_size--;
return harr[0];
}
// Store the minimum value, and remove it from heap
int root = harr[0];
harr[0] = harr[heap_size-1];
heap_size--;
MinHeapify(0);
return root;
}
// This function deletes key at index i. It first reduced value to minus
// infinite, then calls extractMin()
void MinHeap::deleteKey(int i)
{
decreaseKey(i, INT_MIN);
extractMin();
}
// A recursive method to heapify a subtree with the root at given index
// This method assumes that the subtrees are already heapified
void MinHeap::MinHeapify(int i)
{
int l = left(i);
int r = right(i);
int smallest = i;
if (l < heap_size && harr[l] < harr[i])
smallest = l;
if (r < heap_size && harr[r] < harr[smallest])
smallest = r;
if (smallest != i)
{
swap(&harr[i], &harr[smallest]);
MinHeapify(smallest);
}
}
// A utility function to swap two elements
void swap(int *x, int *y)
{
int temp = *x;
*x = *y;
*y = temp;
}
// Driver program to test above functions
int main()
{
MinHeap h(11);
h.insertKey(3);
h.insertKey(2);
h.deleteKey(1);
h.insertKey(15);
h.insertKey(5);
h.insertKey(4);
h.insertKey(45);
cout << h.extractMin() << " ";
cout << h.getMin() << " ";
h.decreaseKey(2, 1);
cout << h.getMin();
return 0;
}
Searching
Traverse the loop to find a target value, requiring safeguards against infinite loops.
For a quick refresher on these operations, try our crash course.
Implementation of Circular Linked Lists
Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.
// Java program for the above approach
import java.util.*;
// A class for Min Heap
class MinHeap {
// To store array of elements in heap
private int[] heapArray;
// max size of the heap
private int capacity;
// Current number of elements in the heap
private int current_heap_size;
// Constructor
public MinHeap(int n) {
capacity = n;
heapArray = new int[capacity];
current_heap_size = 0;
}
// Swapping using reference
private void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
// Get the Parent index for the given index
private int parent(int key) {
return (key - 1) / 2;
}
// Get the Left Child index for the given index
private int left(int key) {
return 2 * key + 1;
}
// Get the Right Child index for the given index
private int right(int key) {
return 2 * key + 2;
}
// Inserts a new key
public boolean insertKey(int key) {
if (current_heap_size == capacity) {
// heap is full
return false;
}
// First insert the new key at the end
int i = current_heap_size;
heapArray[i] = key;
current_heap_size++;
// Fix the min heap property if it is violated
while (i != 0 && heapArray[i] < heapArray[parent(i)]) {
swap(heapArray, i, parent(i));
i = parent(i);
}
return true;
}
// Decreases value of given key to new_val.
// It is assumed that new_val is smaller
// than heapArray[key].
public void decreaseKey(int key, int new_val) {
heapArray[key] = new_val;
while (key != 0 && heapArray[key] < heapArray[parent(key)]) {
swap(heapArray, key, parent(key));
key = parent(key);
}
}
// Returns the minimum key (key at
// root) from min heap
public int getMin() {
return heapArray[0];
}
// Method to remove minimum element
// (or root) from min heap
public int extractMin() {
if (current_heap_size <= 0) {
return Integer.MAX_VALUE;
}
if (current_heap_size == 1) {
current_heap_size--;
return heapArray[0];
}
// Store the minimum value,
// and remove it from heap
int root = heapArray[0];
heapArray[0] = heapArray[current_heap_size - 1];
current_heap_size--;
MinHeapify(0);
return root;
}
// This function deletes key at the
// given index. It first reduced value
// to minus infinite, then calls extractMin()
public void deleteKey(int key) {
decreaseKey(key, Integer.MIN_VALUE);
extractMin();
}
// A recursive method to heapify a subtree
// with the root at given index
// This method assumes that the subtrees
// are already heapified
private void MinHeapify(int key) {
int l = left(key);
int r = right(key);
int smallest = key;
if (l < current_heap_size && heapArray[l] < heapArray[smallest]) {
smallest = l;
}
if (r < current_heap_size && heapArray[r] < heapArray[smallest]) {
smallest = r;
}
if (smallest != key) {
swap(heapArray, key, smallest);
MinHeapify(smallest);
}
}
// Increases value of given key to new_val.
// It is assumed that new_val is greater
// than heapArray[key].
// Heapify from the given key
public void increaseKey(int key, int new_val) {
heapArray[key] = new_val;
MinHeapify(key);
}
// Changes value on a key
public void changeValueOnAKey(int key, int new_val) {
if (heapArray[key] == new_val) {
return;
}
if (heapArray[key] < new_val) {
increaseKey(key, new_val);
} else {
decreaseKey(key, new_val);
}
}
}
// Driver Code
class MinHeapTest {
public static void main(String[] args) {
MinHeap h = new MinHeap(11);
h.insertKey(3);
h.insertKey(2);
h.deleteKey(1);
h.insertKey(15);
h.insertKey(5);
h.insertKey(4);
h.insertKey(45);
System.out.print(h.extractMin() + " ");
System.out.print(h.getMin() + " ");
h.decreaseKey(2, 1);
System.out.print(h.getMin());
}
}
// This code is contributed by rishabmalhdijo
// A class for Min Heap
class MinHeap
{
// Constructor: Builds a heap from a given array a[] of given size
constructor()
{
this.arr = [];
}
left(i) {
return 2*i + 1;
}
right(i) {
return 2*i + 2;
}
parent(i){
return Math.floor((i - 1)/2)
}
getMin()
{
return this.arr[0]
}
insert(k)
{
let arr = this.arr;
arr.push(k);
// Fix the min heap property if it is violated
let i = arr.length - 1;
while (i > 0 && arr[this.parent(i)] > arr[i])
{
let p = this.parent(i);
[arr[i], arr[p]] = [arr[p], arr[i]];
i = p;
}
}
// Decreases value of key at index 'i' to new_val.
// It is assumed that new_val is smaller than arr[i].
decreaseKey(i, new_val)
{
let arr = this.arr;
arr[i] = new_val;
while (i !== 0 && arr[this.parent(i)] > arr[i])
{
let p = this.parent(i);
[arr[i], arr[p]] = [arr[p], arr[i]];
i = p;
}
}
// Method to remove minimum element (or root) from min heap
extractMin()
{
let arr = this.arr;
if (arr.length == 1) {
return arr.pop();
}
// Store the minimum value, and remove it from heap
let res = arr[0];
arr[0] = arr[arr.length-1];
arr.pop();
this.MinHeapify(0);
return res;
}
// This function deletes key at index i. It first reduced value to minus
// infinite, then calls extractMin()
deleteKey(i)
{
this.decreaseKey(i, this.arr[0] - 1);
this.extractMin();
}
// A recursive method to heapify a subtree with the root at given index
// This method assumes that the subtrees are already heapified
MinHeapify(i)
{
let arr = this.arr;
let n = arr.length;
if (n === 1) {
return;
}
let l = this.left(i);
let r = this.right(i);
let smallest = i;
if (l < n && arr[l] < arr[i])
smallest = l;
if (r < n && arr[r] < arr[smallest])
smallest = r;
if (smallest !== i)
{
[arr[i], arr[smallest]] = [arr[smallest], arr[i]]
this.MinHeapify(smallest);
}
}
}
let h = new MinHeap();
h.insert(3);
h.insert(2);
h.deleteKey(1);
h.insert(15);
h.insert(5);
h.insert(4);
h.insert(45);
console.log(h.extractMin() + " ");
console.log(h.getMin() + " ");
h.decreaseKey(2, 1);
console.log(h.extractMin());
# A Python program to demonstrate common binary heap operations
# Import the heap functions from python library
from heapq import heappush, heappop, heapify
# heappop - pop and return the smallest element from heap
# heappush - push the value item onto the heap, maintaining
# heap invarient
# heapify - transform list into heap, in place, in linear time
# A class for Min Heap
class MinHeap:
# Constructor to initialize a heap
def __init__(self):
self.heap = []
def parent(self, i):
return (i-1)/2
# Inserts a new key 'k'
def insertKey(self, k):
heappush(self.heap, k)
# Decrease value of key at index 'i' to new_val
# It is assumed that new_val is smaller than heap[i]
def decreaseKey(self, i, new_val):
self.heap[i] = new_val
while(i != 0 and self.heap[self.parent(i)] > self.heap[i]):
# Swap heap[i] with heap[parent(i)]
self.heap[i] , self.heap[self.parent(i)] = (
self.heap[self.parent(i)], self.heap[i])
# Method to remove minimum element from min heap
def extractMin(self):
return heappop(self.heap)
# This function deletes key at index i. It first reduces
# value to minus infinite and then calls extractMin()
def deleteKey(self, i):
self.decreaseKey(i, float("-inf"))
self.extractMin()
# Get the minimum element from the heap
def getMin(self):
return self.heap[0]
# Driver pgoratm to test above function
heapObj = MinHeap()
heapObj.insertKey(3)
heapObj.insertKey(2)
heapObj.deleteKey(1)
heapObj.insertKey(15)
heapObj.insertKey(5)
heapObj.insertKey(4)
heapObj.insertKey(45)
print heapObj.extractMin(),
print heapObj.getMin(),
heapObj.decreaseKey(2, 1)
print heapObj.getMin()
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
Output Explanation
For all implementations:
- Sequence: Insert 3, 2; delete index 1; insert 15, 5, 4, 45; extract min (2); get min (4); decrease key at index 2 to 1; get min (1).
- Result: 2 4 1
These examples showcase how Min Heaps are implemented across different languages, each leveraging language-specific features while maintaining the core heap properties.
Real-World Applications of Binary Heaps
Binary Heaps are powerhouse tools across programming domains:
- Heap Sort: A sorting algorithm leveraging heaps to order data in O(N log N) time.
- Priority Queues: Perfect for scheduling tasks or managing bandwidth, with fast access to top-priority items.
- Graph Algorithms: Essential for Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree.
- Finding Extremes: Quickly pinpoint the K’th largest or smallest element.
- Merging Arrays: Efficiently combine multiple sorted arrays.
Curious how heaps enhance system design or web projects? Explore our Master DSA, Web Dev, System Design and Web Development courses.
Min Heap vs. Max Heap: What’s the Difference?
While both are Binary Heaps, their priorities diverge:
- Here’s the comparison in a Markdown table:
Difference | Min‑Heap | Max‑Heap |
1. Root node comparison | In a Min‑Heap, the key at the root must be ≤ all of its children. | In a Max‑Heap, the key at the root must be ≥ all of its children. |
2. Root element | The minimum key element is at the root. | The maximum key element is at the root. |
3. Priority order | Uses ascending priority. | Uses descending priority. |
4. Construction priority | During heap construction, the smallest element has priority. | During heap construction, the largest element has priority. |
5. Element removal | The smallest element is the first to be popped. | The largest element is the first to be popped. |
Choosing between them depends on your problem—need the best performer or the weakest link? For deeper insights, check out our Data Science course.
Performance Breakdown
Binary Heaps deliver stellar efficiency:
- Get Min/Max: O(1)—instant root access.
- Insert: O(log N)—logarithmic bubbling.
- Delete Min/Max: O(log N)—heapify restores order.
This balance of speed and simplicity makes heaps a staple in algorithm design. Prep for heap-related interview questions with our Crash Course.
Frequently Asked Questions
How does a Binary Heap differ from a Binary Search Tree?
A Binary Heap enforces the heap property for priority access, while a Binary Search Tree maintains sorted order for searches. Learn more in our DSA course.
Can Binary Heaps sort data?
Absolutely! Heap Sort uses a heap to sort in O(N log N) time. Dive into it with our Web Development course.
How do I build a Priority Queue with a Heap?
Use a Min Heap for smallest-first or a Max Heap for largest-first queues. Our Design DSA Combined course covers practical implementations.
What are advanced heap variants?
Binomial and Fibonacci Heaps optimize specific operations. Explore them in our Master DSA, Web Dev, System Design course.
How can I ace heap questions in interviews?
Practice core operations and applications like Heap Sort. Our Data Science course offers tailored exercises.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Essentials of Machine Learning and Artificial Intelligence
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 22+ Hands-on Live Projects & Deployments
- Comprehensive Notes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 57% OFF
₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 60% OFF
₹15,000.00 ₹5,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085