Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Binary Indexed Tree (Fenwick Tree) Explained
Introduction to Binary Indexed Tree
A Binary Indexed Tree, also known as a Fenwick Tree, is a data structure designed to efficiently perform operations on a fixed-size array. It is particularly useful for scenarios where we need to handle multiple operations like:
- Prefix operations (such as Sum, Product, XOR, OR, etc.)
It’s important to note that many range operations can be reduced to prefix operations. For example, to calculate the range sum from index L to R, we can compute the prefix sum up to R and subtract the prefix sum up to L – 1.
Additionally, Binary Indexed Trees are ideal for cases where we need to:
- Update the value of a specific array element.
Both prefix query and update operations can be performed in O(log n) time. To initialize the tree, we require O(n log n) preprocessing time and O(n) auxiliary space.
Example Problem to Understand Binary Indexed Tree
To better grasp how Binary Indexed Trees work, let’s look at a simple example problem.
Suppose we are given an array arr[0 … n-1]. We want to perform two operations efficiently:
- Compute the sum of the first i elements.
- Update the value of a specific element in the array such that arr[i] = x, where 0 <= i <= n-1.
For comprehensive DSA practice, consider enrolling in our DSA course to master these concepts.
Efficient Solutions for Range Sum and Updates
Brute Force and Prefix Sum Approaches
A straightforward approach to compute the sum of the first i elements is to run a loop from 0 to i – 1 and add the values. Updating an element is simple with arr[i] = x.
- Time complexity:
- Query: O(n)
- Update: O(1)
Another basic method is to maintain an auxiliary array where each index holds the sum of the first i elements of the original array. This enables range sum queries in O(1) time. However, every time an element is updated, the entire prefix sum array must be recalculated.
- Time complexity:
- Query: O(1)
- Update: O(n)
This technique is efficient when there are many queries but very few updates.
Can We Achieve O(log n) for Both Operations?
Yes, it’s possible to perform both query and update operations in O(log n) time.
One optimized solution is the Segment Tree, which handles both operations efficiently in O(log n) time.
An alternative and more space-efficient structure is the Binary Indexed Tree (BIT), also known as Fenwick Tree. It provides the same O(log n) time complexity for both operations but is simpler to implement and requires less memory.
Binary Indexed Tree: Representation and Construction
Representation
A Binary Indexed Tree is implemented as an array named BITree[]. Each element in this tree stores the sum of a subset of elements from the input array.
- The size of BITree[] is n, where n is the size of the input array.
- For convenience in implementation, we typically use an array of size n + 1.
Construction
To build the BITree, we start by initializing all elements in BITree[] to zero. Then, we invoke the update() function on all indices, which is explained in the next section.
If you aim to build a strong foundation in data structures for web applications or system design, explore our Essential DSA & Web Dev courses to integrate these skills.
Operations in Binary Indexed Tree
getSum(x): Compute Prefix Sum
This function returns the sum of the sub-array arr[0 … x] using the already constructed BITree[].
Steps to compute getSum(x):
- Initialize the result sum as 0, and the index as x + 1.
- While the index is greater than 0, do the following:
- a) Add BITree[index] to sum.
- b) Move to the parent index using the formula:
index = index – (index & -index)
- Return the final sum.
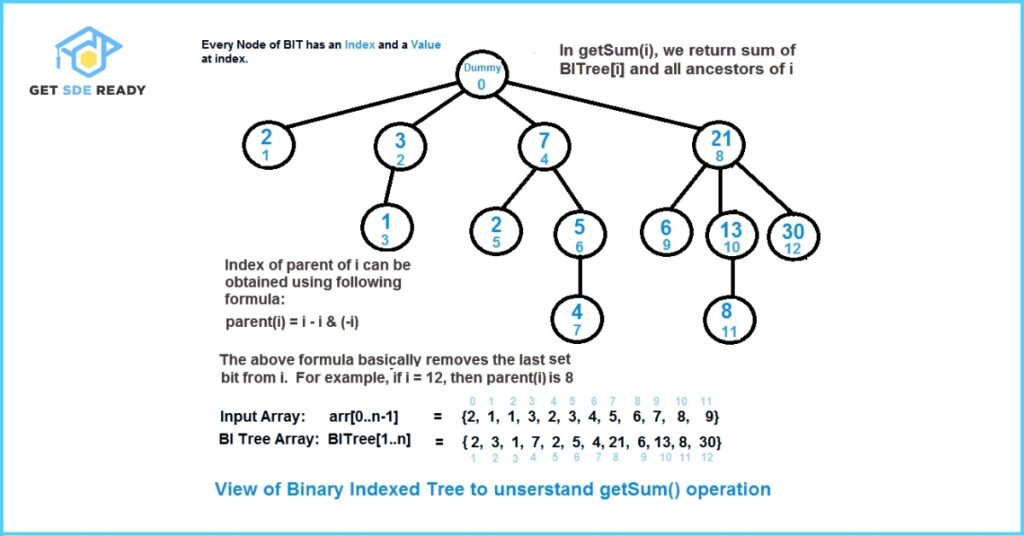
Understanding getSum() with a Binary Indexed Tree
Diagram Explanation and Key Observations
The diagram above illustrates how the getSum() function works in a Binary Indexed Tree (BIT). Based on the diagram, here are a few important takeaways:
- BITree[0] is a dummy node
It is not used for any calculation and typically holds no useful data. The BIT usually starts indexing from 1 for easier bit manipulation. - BITree[y] is the parent of BITree[x]
This relationship holds only if y can be derived by removing the last set bit from the binary representation of x.
Mathematically, this can be expressed as:
y = x – (x & (-x)) - BITree[x] stores the partial sum between y and x
The child node BITree[x] contains the sum of the array elements from index y (inclusive) to x (exclusive).
In notation:
BITree[x] = sum of arr[y, …, x)
Update(x, val): Updating the Binary Indexed Tree
Function Purpose
The update(x, val) function is used to modify the Binary Indexed Tree (BITree[]) by updating it with a given value. This operation reflects the change in the prefix sums stored in the tree.
⚠️ Note: This operation does not modify the original array arr[]. It only updates the corresponding values in the BITree[].
Steps to Perform update(x, val)
- Initialize the index as x + 1.
(Since the BIT is typically 1-based indexed, we adjust the index accordingly.) - While the current index is less than or equal to n, repeat the following steps:
- a) Add val to BITree[index].
- b) Move to the next index by adding the last set bit of the current index.
This is done using the formula:
index = index + (index & (-index))
By following this method, only the necessary nodes in the BITree[] are updated, maintaining the efficiency of the structure with a time complexity of O(log n).
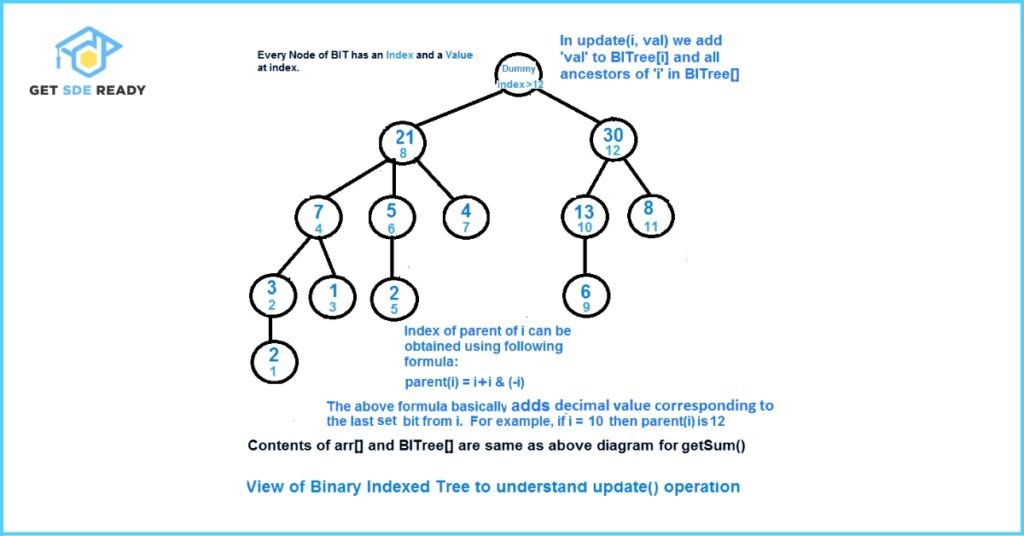
How the update() Function Works in Binary Indexed Tree
Updating Relevant Nodes in BITree
The update() function is designed to ensure that all relevant nodes in the Binary Indexed Tree (BITree[]) that include arr[i] in their range are updated properly. To achieve this, the function iterates over each affected node by continuously adding the decimal value of the last set bit of the current index.
This technique guarantees that every node which contributes to prefix queries involving arr[i] is appropriately updated.
How Does a Binary Indexed Tree Work?
Core Principle Behind BITree
The underlying concept of a Binary Indexed Tree is rooted in the fact that every positive integer can be expressed as a sum of powers of 2.
For example:
19 = 16 + 2 + 1 (i.e., 2⁴ + 2¹ + 2⁰)
Each node in the BITree[] maintains the sum of a range of elements, where the size of the range is a power of 2.
Let’s revisit the example shown in the getSum() diagram:
- To compute the sum of the first 12 elements, we:
- Add the sum of elements 9 to 12 (which is 4 elements, i.e., 2²)
- Plus the sum of elements 1 to 8 (which is 8 elements, i.e., 2³)
This highlights how BITree leverages binary representation for efficient querying.
Why is BITree Efficient?
- The number of set bits in the binary form of any number n is O(log n).
- Therefore, both the getSum() and update() operations involve traversing at most O(log n) nodes.
Time Complexity
- Query and Update: O(log n)
- Construction Time: O(n log n), as it calls the update() function for all n elements during tree construction.
Implementation
Below is the actual implementation of the Binary Indexed Tree, demonstrating both update and query operations.
// C++ code to demonstrate operations of Binary Index Tree
#include <iostream>
using namespace std;
/* n --> No. of elements present in input array.
BITree[0..n] --> Array that represents Binary Indexed Tree.
arr[0..n-1] --> Input array for which prefix sum is evaluated. */
// Returns sum of arr[0..index]. This function assumes
// that the array is preprocessed and partial sums of
// array elements are stored in BITree[].
int getSum(int BITree[], int index)
{
int sum = 0; // Initialize result
// index in BITree[] is 1 more than the index in arr[]
index = index + 1;
// Traverse ancestors of BITree[index]
while (index>0)
{
// Add current element of BITree to sum
sum += BITree[index];
// Move index to parent node in getSum View
index -= index & (-index);
}
return sum;
}
// Updates a node in Binary Index Tree (BITree) at given index
// in BITree. The given value 'val' is added to BITree[i] and
// all of its ancestors in tree.
void updateBIT(int BITree[], int n, int index, int val)
{
// index in BITree[] is 1 more than the index in arr[]
index = index + 1;
// Traverse all ancestors and add 'val'
while (index <= n)
{
// Add 'val' to current node of BI Tree
BITree[index] += val;
// Update index to that of parent in update View
index += index & (-index);
}
}
// Constructs and returns a Binary Indexed Tree for given
// array of size n.
int *constructBITree(int arr[], int n)
{
// Create and initialize BITree[] as 0
int *BITree = new int[n+1];
for (int i=1; i<=n; i++)
BITree[i] = 0;
// Store the actual values in BITree[] using update()
for (int i=0; i<n; i++)
updateBIT(BITree, n, i, arr[i]);
// Uncomment below lines to see contents of BITree[]
//for (int i=1; i<=n; i++)
// cout << BITree[i] << " ";
return BITree;
}
// Driver program to test above functions
int main()
{
int freq[] = {2, 1, 1, 3, 2, 3, 4, 5, 6, 7, 8, 9};
int n = sizeof(freq)/sizeof(freq[0]);
int *BITree = constructBITree(freq, n);
cout << "Sum of elements in arr[0..5] is "
<< getSum(BITree, 5);
// Let use test the update operation
freq[3] += 6;
updateBIT(BITree, n, 3, 6); //Update BIT for above change in arr[]
cout << "\nSum of elements in arr[0..5] after update is "
<< getSum(BITree, 5);
return 0;
}
Searching
Traverse the loop to find a target value, requiring safeguards against infinite loops.
For a quick refresher on these operations, try our crash course.
Implementation of Circular Linked Lists
Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.
// Java program to demonstrate lazy
// propagation in segment tree
import java.util.*;
import java.lang.*;
import java.io.*;
class BinaryIndexedTree
{
// Max tree size
final static int MAX = 1000;
static int BITree[] = new int[MAX];
/* n --> No. of elements present in input array.
BITree[0..n] --> Array that represents Binary
Indexed Tree.
arr[0..n-1] --> Input array for which prefix sum
is evaluated. */
// Returns sum of arr[0..index]. This function
// assumes that the array is preprocessed and
// partial sums of array elements are stored
// in BITree[].
int getSum(int index)
{
int sum = 0; // Initialize result
// index in BITree[] is 1 more than
// the index in arr[]
index = index + 1;
// Traverse ancestors of BITree[index]
while(index>0)
{
// Add current element of BITree
// to sum
sum += BITree[index];
// Move index to parent node in
// getSum View
index -= index & (-index);
}
return sum;
}
// Updates a node in Binary Index Tree (BITree)
// at given index in BITree. The given value
// 'val' is added to BITree[i] and all of
// its ancestors in tree.
public static void updateBIT(int n, int index,
int val)
{
// index in BITree[] is 1 more than
// the index in arr[]
index = index + 1;
// Traverse all ancestors and add 'val'
while(index <= n)
{
// Add 'val' to current node of BIT Tree
BITree[index] += val;
// Update index to that of parent
// in update View
index += index & (-index);
}
}
/* Function to construct fenwick tree
from given array.*/
void constructBITree(int arr[], int n)
{
// Initialize BITree[] as 0
for(int i=1; i<=n; i++)
BITree[i] = 0;
// Store the actual values in BITree[]
// using update()
for(int i = 0; i < n; i++)
updateBIT(n, i, arr[i]);
}
// Main function
public static void main(String args[])
{
int freq[] = {2, 1, 1, 3, 2, 3,
4, 5, 6, 7, 8, 9};
int n = freq.length;
BinaryIndexedTree tree = new BinaryIndexedTree();
// Build fenwick tree from given array
tree.constructBITree(freq, n);
System.out.println("Sum of elements in arr[0..5]"+
" is "+ tree.getSum(5));
// Let use test the update operation
freq[3] += 6;
// Update BIT for above change in arr[]
updateBIT(n, 3, 6);
// Find sum after the value is updated
System.out.println("Sum of elements in arr[0..5]"+
" after update is " + tree.getSum(5));
}
}
// This code is contributed by Ranjan Binwani
class SegmentTree:
def __init__(self, data):
self.n = len(data)
self.tree = [0] * (2 * self.n)
self.build(data)
def build(self, data):
for i in range(self.n):
self.tree[self.n + i] = data[i]
for i in range(self.n - 1, 0, -1):
self.tree[i] = self.tree[i * 2] + self.tree[i * 2 + 1]
def update(self, idx, value):
idx += self.n
self.tree[idx] = value
i = idx
while i > 1:
self.tree[i // 2] = self.tree[i] + self.tree[i ^ 1]
i //= 2
def query(self, l, r):
res = 0
l += self.n
r += self.n
while l < r:
if l & 1:
res += self.tree[l]
l += 1
if r & 1:
r -= 1
res += self.tree[r]
l //= 2
r //= 2
return res
# Example Usage
data = [2, 4, 1, 3, 5]
seg_tree = SegmentTree(data)
print(seg_tree.query(1, 4)) # Output: 8
seg_tree.update(2, 6)
print(seg_tree.query(1, 4)) # Output: 13
<script>
// Javascript program to demonstrate lazy
// propagation in segment tree
// Max tree size
let MAX = 1000;
let BITree=new Array(MAX);
/* n --> No. of elements present in input array.
BITree[0..n] --> Array that represents Binary
Indexed Tree.
arr[0..n-1] --> Input array for which prefix sum
is evaluated. */
// Returns sum of arr[0..index]. This function
// assumes that the array is preprocessed and
// partial sums of array elements are stored
// in BITree[].
function getSum( index)
{
let sum = 0; // Initialize result
// index in BITree[] is 1 more than
// the index in arr[]
index = index + 1;
// Traverse ancestors of BITree[index]
while(index>0)
{
// Add current element of BITree
// to sum
sum += BITree[index];
// Move index to parent node in
// getSum View
index -= index & (-index);
}
return sum;
}
// Updates a node in Binary Index Tree (BITree)
// at given index in BITree. The given value
// 'val' is added to BITree[i] and all of
// its ancestors in tree.
function updateBIT(n,index,val)
{
// index in BITree[] is 1 more than
// the index in arr[]
index = index + 1;
// Traverse all ancestors and add 'val'
while(index <= n)
{
// Add 'val' to current node of BIT Tree
BITree[index] += val;
// Update index to that of parent
// in update View
index += index & (-index);
}
}
/* Function to construct fenwick tree
from given array.*/
function constructBITree(arr,n)
{
// Initialize BITree[] as 0
for(let i=1; i<=n; i++)
BITree[i] = 0;
// Store the actual values in BITree[]
// using update()
for(let i = 0; i < n; i++)
updateBIT(n, i, arr[i]);
}
// Main function
let freq=[2, 1, 1, 3, 2, 3,
4, 5, 6, 7, 8, 9];
let n = freq.length;
// Build fenwick tree from given array
constructBITree(freq, n);
document.write("Sum of elements in arr[0..5]"+
" is "+ getSum(5)+"<br>");
// Let use test the update operation
freq[3] += 6;
// Update BIT for above change in arr[]
updateBIT(n, 3, 6);
// Find sum after the value is updated
document.write("Sum of elements in arr[0..5]"+
" after update is " + getSum(5));
// This code is contributed by patel2127
</script>
Output and Performance of Binary Indexed Tree
Sample Output
Sum of elements in arr[0..5] is 12
Sum of elements in arr[0..5] after update is 18
Time and Space Complexity
- Time Complexity: O(N log N)
- Auxiliary Space: O(N)
Can Binary Indexed Tree Handle Range Sum Queries in O(log n) Time?
Efficient Range Sum with BIT
Yes, Binary Indexed Trees can efficiently compute range sums in O(log n) time using the formula:
rangeSum(l, r) = getSum(r) – getSum(l – 1)
This approach uses the same prefix sum logic we’ve implemented earlier, enabling fast and efficient retrieval of any subarray sum.
Applications of Binary Indexed Tree
Real-World Use Cases
One of the major applications of Binary Indexed Trees lies in the implementation of arithmetic coding algorithms. In fact, the structure was originally developed specifically for this purpose.
For hands-on projects and integrating data structures into full-stack work, explore our Web Development course or the combined Master DSA, Web Dev & System Design.
FAQs
What is a Binary Indexed Tree?
A Binary Indexed Tree is a data structure that provides fast prefix queries and point updates on an array, both in O(log n) time.
How do I get a subarray sum with BIT?
Compute two prefix sums and subtract: sum(0…R) – sum(0…L-1). Each prefix query is O(log n), so the range sum is O(log n).
Can BIT handle updates efficiently?
Yes. When an element changes, you propagate the change through relevant tree nodes in O(log n), keeping prefix queries accurate.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Essentials of Machine Learning and Artificial Intelligence
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 22+ Hands-on Live Projects & Deployments
- Comprehensive Notes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 57% OFF
₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 60% OFF
₹15,000.00 ₹5,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085
