Power Analysis & Confidence Intervals

When we make decisions based on data, we want those decisions to be statistically reliable. Confidence intervals help us understand the range in which a result is likely to fall, while Power Analysis helps us decide how much data we need before even starting an experiment.

Confidence Intervals (CIs)

A Confidence Interval is a range of values that’s likely to contain the true population parameter (like the mean) with a certain level of confidence (usually 95%).

Key Concepts:

• Point Estimate: Sample statistic (like mean)
• Margin of Error: Based on sample variability and size
• Confidence Level: How sure we are (e.g., 95%)

Formula (for mean):

CI=xˉ±z∗(σn)text{CI} = bar{x} pm z^* left(frac{sigma}{sqrt{n}}right)CI=xˉ±z∗(n​σ​)

Where:

• xˉbar{x}xˉ = sample mean
• z∗z^*z∗ = z-score (e.g., 1.96 for 95%)
• $\sigma$ = standard deviation
• $n$ = sample size

Example:

You analyze Zomato delivery times for a city. The sample mean is 32 mins. With 95% confidence, the delivery time is between 30 to 34 minutes. That’s the confidence interval.

Interpreting Confidence Intervals

• A 95% confidence interval means: “If we repeated this study 100 times, the true mean would lie within our interval 95 times.”
• Narrower intervals = more precision → comes from larger sample size or lower variability

Power Analysis

Power is the probability that your test will detect an effect when there is one (i.e., reject H₀ correctly). It helps in planning experiments.

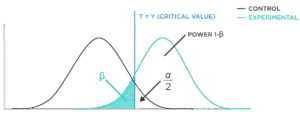
Why Power Matters:

• Avoids Type II error (false negative)
• Helps determine how large a sample size you need

A typical goal:

• Power ≥ 0.8 → means you have an 80% chance of detecting a real effect

Factors affecting Power

1. Effect size – how big the expected difference is
2. Sample size – more data → higher power
3. Significance level (α) – usually 0.05
4. Variability in the data

Real-Life Example:

Imagine you work at Cult.Fit and want to test a new app layout to improve user engagement.

• You expect a 10% increase in workout sessions.
• Power analysis tells you: “To detect this effect with 80% power at α = 0.05, you need 500 users per group.”

Without enough power, your test may fail to detect real improvements—even if they exist.

Summary:

• Confidence Interval → Helps you report results with a margin of certainty.
• Power Analysis → Helps you design experiments effectively before starting.