Z-Score and Central Limit Theorem (CLT)

Understanding Z-scores and the Central Limit Theorem is foundational for working with probabilities, normal distributions, and any kind of statistical inference in analytics.

What is a Z-Score?

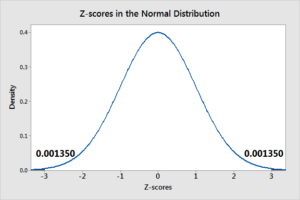
A Z-score tells us how far a data point is from the mean in terms of standard deviations.

Formula:

Z=(X−μ)σZ = frac{(X – mu)}{sigma}Z=σ(X−μ)

​

• $X$ = raw score
• $\mu$ = mean of the population
• $\sigma$ = standard deviation

Interpretation:

• Z = 0 → Exactly at the mean
• Z > 0 → Above the mean
• Z < 0 → Below the mean
• Z = 2 → Two standard deviations above the mean

Example:

If the average delivery time on Swiggy is 30 minutes with a standard deviation of 5 minutes, a 40-minute delivery would have:

Z=(40−30)5=2Z = frac{(40 – 30)}{5} = 2Z=5(40−30)​=2

This means it’s 2 standard deviations above the average.

Why It Matters:

Z-scores help identify outliers, compare values across different datasets, and are used in probability calculations involving the normal distribution.

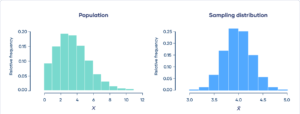
What is the Central Limit Theorem (CLT)?

The Central Limit Theorem is one of the most powerful ideas in statistics. It says:

When you take random samples of a sufficient size (usually n ≥ 30) from any population, the distribution of the sample means will be approximately normal, regardless of the population’s distribution.

Key Insights:

• The mean of the sampling distribution will be equal to the population mean ($\mu$).
• The standard deviation of the sampling distribution (called standard error) is:

SE=σnSE = frac{sigma}{sqrt{n}}SE=n​σ​

Example:

Suppose you collect random samples of 100 Zomato delivery times (from a skewed population). According to CLT, the distribution of the sample averages will look like a bell curve (normal distribution) even though the original data is not.

Z-Score + CLT in Real Analytics

1. CLT allows us to make predictions and confidence intervals using sample means.
2. Z-scores help us calculate probabilities under the normal curve (using tables or Python libraries).
3. Together, they make A/B testing, customer segmentation, and performance benchmarking statistically reliable.