Peterson’s Solution & Bakery Algorithm
In concurrent programming, ensuring that only one process accesses a critical section at a time is crucial to prevent race conditions. While modern systems use hardware support or synchronization primitives (like mutexes), some classical software-based algorithms help us understand how mutual exclusion can be achieved using basic logic and variables alone.
Two of the most well-known classical solutions are:
- Peterson’s Solution — for two-process mutual exclusion
- Bakery Algorithm — for multiple-process mutual exclusion
These algorithms are important from both a theoretical and foundational perspective in operating systems and concurrent computing.
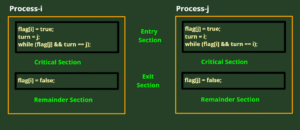
Peterson’s Solution (Two-Process Mutual Exclusion)
Peterson’s Solution is a software-based algorithm designed to allow two processes to share a single-use resource without conflict using only shared memory and two variables.
Key Concepts:
- It ensures mutual exclusion: only one process enters the critical section at a time.
- It provides progress: if one process is not interested, the other is allowed.
- It maintains bounded waiting: each process gets its turn eventually.
Working Mechanism:
The algorithm uses:
- A boolean array
flag[2]to indicate if a process wants to enter the critical section. - An integer variable
turnto indicate whose turn it is.
Each process:
- Sets its flag to
true(it wants to enter). - Sets
turnto the other process. - Waits until the other process doesn’t want to enter or it’s their turn.
Why it’s important:
Peterson’s Solution is a simple yet powerful example of mutual exclusion achieved purely in software, without needing atomic hardware instructions.
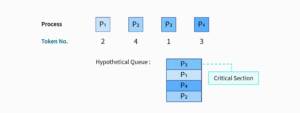
Bakery Algorithm (N-Process Mutual Exclusion)
Developed by Leslie Lamport, the Bakery Algorithm generalizes Peterson’s logic to any number of processes, similar to a bakery where customers take numbered tokens to be served.
Key Concepts:
- Every process takes a number (like taking a token in a bakery).
- The process with the smallest number gets to enter the critical section.
- If two processes have the same number, the one with the smaller process ID goes first.
Working Mechanism:
- Each process chooses a number greater than any other number currently in use.
- Before entering the critical section, it waits for all other processes with a lower number (or same number but lower ID) to finish.
- After exiting, it resets its number to 0.
Why it matters:
The Bakery Algorithm ensures:
- Mutual exclusion
- Fairness (no starvation)
- Scalability to multiple processes
It’s a foundational example in distributed systems and OS theory for ensuring fair and safe access to shared resources.
Summary Table
| Feature | Peterson’s Solution | Bakery Algorithm |
|---|---|---|
| Applicable For | 2 processes only | Multiple processes (n ≥ 2) |
| Uses Turn Variable | Yes | No |
| Fairness | Yes | Yes |
| Mutual Exclusion | Guaranteed | Guaranteed |
| Starvation-Free | Yes | Yes |
| Complexity | Low | Higher (due to numbering logic) |