Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Shortest Path Algorithm Tutorial with Problems
Given a weighted graph represented by an n x n matrix dist[][], where each element dist[i][j] indicates the weight of the direct edge from node i to node j, your goal is to find the shortest distance between every pair of nodes (i, j).
Important Details:
- If there is no direct edge between two nodes i and j, the value dist[i][j] is set to a large number ( such as 108 ) to symbolize infinity.
- The diagonal entries dist[i][i] are always zero, reflecting the fact that the distance from any node to itself is zero.
- The graph can contain negative edge weights, but no negative weight cycles exist.
Problem Statement:
Calculate the shortest path distances between all pairs of nodes in the graph, taking into account every possible intermediate node.
Example:
Input: dist[][]
| 0 | 4 | 108 | 5 | 108 |
| 108 | 0 | 1 | 108 | 6 |
| 2 | 108 | 0 | 3 | 108 |
| 108 | 108 | 1 | 0 | 2 |
| 1 | 108 | 108 | 4 | 0 |
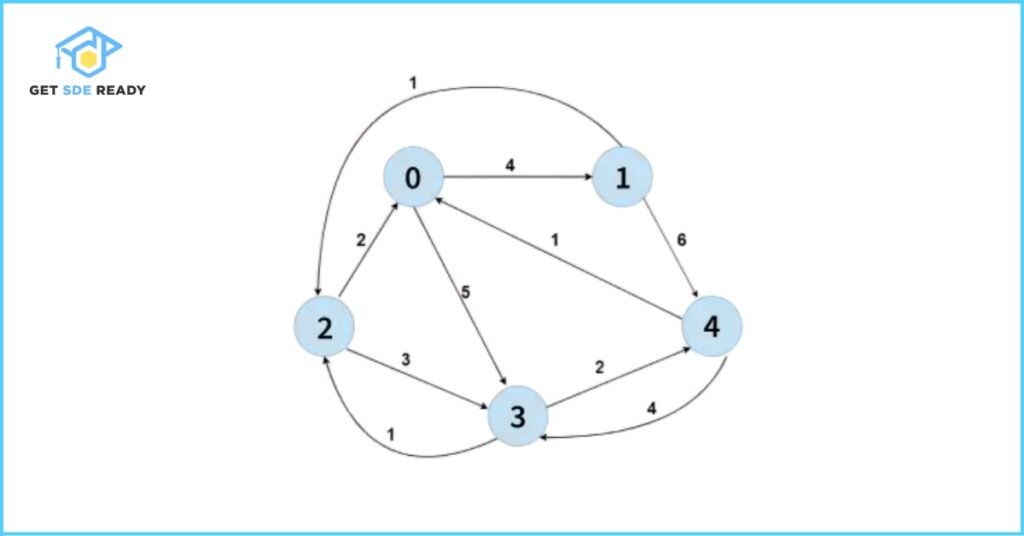
| 0 | 4 | 5 | 5 | 7 |
| 3 | 0 | 1 | 4 | 6 |
| 2 | 6 | 0 | 3 | 5 |
| 3 | 7 | 1 | 0 | 2 |
| 1 | 5 | 5 | 4 | 0 |
Explanation:
The output matrix shows the shortest distances between all pairs of nodes. Each element dist[i][j] in the result represents the minimal cost to travel from node i to node j. This result is achieved by applying the Floyd-Warshall algorithm, which systematically considers all possible intermediate nodes to update the shortest path estimates.
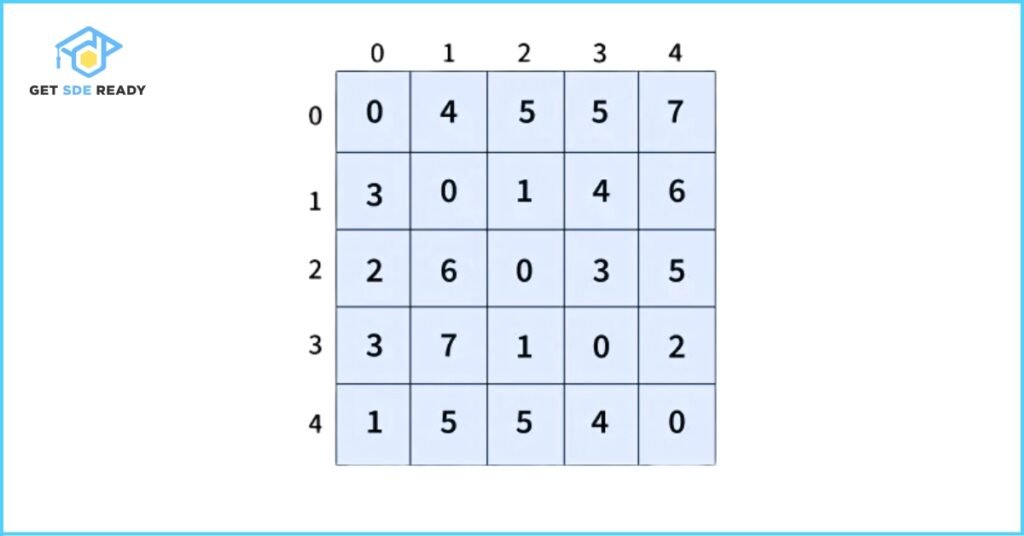
Floyd-Warshall Algorithm: Overview and Working Principle
The Floyd–Warshall algorithm is a classic method to find the shortest distances between every pair of nodes in a weighted graph. It works by maintaining a two-dimensional array that stores the shortest distances between nodes. Initially, this array is filled using the direct edge weights between nodes. The algorithm then iteratively updates these distances by checking if including intermediate nodes results in shorter paths.
This algorithm works for both directed and undirected weighted graphs, and it supports graphs with positive and negative edge weights.
Note: The Floyd-Warshall algorithm does not work for graphs containing negative weight cycles — cycles where the sum of edges is negative — since shortest paths in such graphs are undefined.
Core Idea Behind the Floyd-Warshall Algorithm
Problem Setup
Suppose we have a graph represented by an dist[][] matrix with V vertices numbered from 0 to V-1. The goal is to compute the shortest path distances between all pairs (i, j) of vertices.
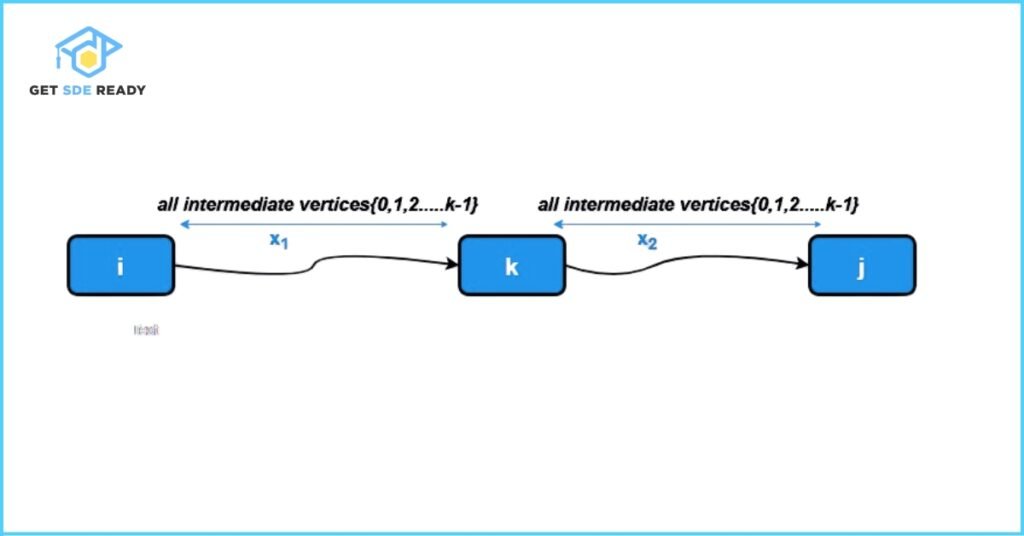
Incremental Inclusion of Intermediate Vertices
Assume the path from vertex i to vertex j may include some intermediate nodes. The key idea of the Floyd-Warshall algorithm is to treat each vertex k as a potential intermediate node, one at a time.
- When considering vertex k, the algorithm assumes that all vertices from 0 to k-1 have already been used as intermediate nodes.
- Using the shortest paths computed for vertices less than k, it updates the distances by checking if routing through k produces a shorter path.
By iteratively incorporating each vertex as an intermediate node, the algorithm progressively builds up the shortest path distances.
Optimal Substructure in Floyd-Warshall Algorithm
The Floyd-Warshall algorithm relies on the optimal substructure property, which states:
- The shortest path between two vertices either excludes the intermediate vertex k, or
- Includes the intermediate vertex k, in which case the path can be split into two parts: from i to k, and from k to j.
By applying this principle for all vertices k, the algorithm ensures the resulting distance matrix contains the shortest possible distances between all node pairs.
Why Floyd-Warshall Algorithm Works (Correctness Proof)
The Floyd-Warshall algorithm is founded on the principle of optimal substructure, which means:
- If the shortest path from vertex i to vertex j passes through some vertex k, then the path from i to k and the path from k to j must themselves be shortest paths.
- The algorithm’s iterative approach guarantees that by the time vertex k is considered as an intermediate node, all shortest paths involving only vertices from 0 to k-1 have already been computed.
- Consequently, by the end of the process, the algorithm computes all shortest paths optimally because it systematically evaluates every possible intermediate vertex.
Why Floyd-Warshall Is Better for Dense Graphs and Not for Sparse Graphs
Dense vs Sparse Graphs
- Dense Graph: A graph where the number of edges is significantly higher relative to the number of vertices.
- Sparse Graph: A graph with relatively few edges compared to the number of vertices.
Performance Considerations
Floyd-Warshall runs in O(V³) time, regardless of the number of edges. This makes it ideal for dense graphs, where many edges exist, and the cubic complexity is acceptable given the high connectivity.
For sparse graphs, where edges are few, other algorithms like Johnson’s Algorithm or Dijkstra’s Algorithm with priority queues tend to be more efficient because they exploit the sparsity to avoid unnecessary computations.
Step-by-Step Implementation of Floyd-Warshall Algorithm
- Initialize the distance matrix: Use the direct edge weights as initial distances. For pairs without direct edges, use a large number to represent infinity.
- Iterate through each vertex k: Treat vertex k as a potential intermediate node between all pairs (i, j).
- For each pair (i, j): There are two cases:
- Case 1: The shortest path from i to j does not go through vertex k. Keep dist[i][j] as is.
- Case 2: The shortest path does go through vertex k. Update dist[i][j] to dist[i][k] + dist[k][j] if this is shorter than the current distance.
- Case 1: The shortest path from i to j does not go through vertex k. Keep dist[i][j] as is.
- Repeat: Continue this process for all vertices k until all possible intermediate nodes have been considered.
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
void floydWarshall(vector<vector<int>> &dist) {
int V = dist.size();
// Add all vertices one by one to
// the set of intermediate vertices.
for (int k = 0; k < V; k++) {
// Pick all vertices as source one by one
for (int i = 0; i < V; i++) {
// Pick all vertices as destination
// for the above picked source
for (int j = 0; j < V; j++) {
// shortest path from
// i to j
if(dist[i][k] != 1e8 && dist[k][j]!= 1e8)
dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);
}
}
}
}
int main() {
int INF = 100000000;
vector<vector<int>> dist = {
{0, 4, INF, 5, INF},
{INF, 0, 1, INF, 6},
{2, INF, 0, 3, INF},
{INF, INF, 1, 0, 2},
{1, INF, INF, 4, 0}
};
floydWarshall(dist);
for(int i = 0; i<dist.size(); i++) {
for(int j = 0; j<dist.size(); j++) {
cout<<dist[i][j]<<" ";
}
cout<<endl;
}
return 0;
}
Searching
Traverse the loop to find a target value, requiring safeguards against infinite loops.
For a quick refresher on these operations, try our crash course.
Implementation of Circular Linked Lists
Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
static void floydWarshall(int[][] dist){
int V = dist.length;
// Add all vertices one by one to
// the set of intermediate vertices.
for (int k = 0; k < V; k++) {
// Pick all vertices as source one by one
for (int i = 0; i < V; i++) {
// Pick all vertices as destination
// for the above picked source
for (int j = 0; j < V; j++) {
// shortest path from
// i to j
if(dist[i][k] != 1e8 && dist[k][j]!= 1e8)
dist[i][j] = Math.min(dist[i][j],dist[i][k] + dist[k][j]);
}
}
}
}
public static void main(String[] args)
{
int INF = 100000000;
int[][] dist = { { 0, 4, INF, 5, INF },
{ INF, 0, 1, INF, 6 },
{ 2, INF, 0, 3, INF },
{ INF, INF, 1, 0, 2 },
{ 1, INF, INF, 4, 0 } };
floydWarshall(dist);
for (int i = 0; i < dist.length; i++) {
for (int j = 0; j < dist.length; j++) {
System.out.print(dist[i][j] + " ");
}
System.out.println();
}
}
}
// Solves the all-pairs shortest path
// problem using Floyd Warshall algorithm
function floydWarshall(dist)
{
let V = dist.length;
// Add all vertices one by one to
// the set of intermediate vertices.
for (let k = 0; k < V; k++) {
// Pick all vertices as source one by one
for (let i = 0; i < V; i++) {
// Pick all vertices as destination
// for the above picked source
for (let j = 0; j < V; j++) {
// shortest path from
// i to j
if (dist[i][k] != INF && dist[k][j] != INF) {
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
}
let INF = 100000000;
// Driver Code
let dist = [
[0, 4, INF, 5, INF],
[INF, 0, 1, INF, 6],
[2, INF, 0, 3, INF],
[INF, INF, 1, 0, 2],
[1, INF, INF, 4, 0]
];
floydWarshall(dist);
for (let i = 0; i < dist.length; i++) {
console.log(dist[i].join(" "));
}
# Solves the all-pairs shortest path
# problem using Floyd Warshall algorithm
def floydWarshall(dist):
V = len(dist)
# Add all vertices one by one to
# the set of intermediate vertices.
for k in range(V):
# Pick all vertices as source one by one
for i in range(V):
# Pick all vertices as destination
# for the above picked source
for j in range(V):
#shortest path from
#i to j
if(dist[i][k] != 100000000 and dist[k][j]!= 100000000):
dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);
if __name__ == "__main__":
INF = 100000000;
dist = [
[0, 4, INF, 5, INF],
[INF, 0, 1, INF, 6],
[2, INF, 0, 3, INF],
[INF, INF, 1, 0, 2],
[1, INF, INF, 4, 0]
]
floydWarshall(dist)
for i in range(len(dist)):
for j in range(len(dist)):
print(dist[i][j], end=" ")
print()
Output: Shortest Path Distance Matrix
3 0 1 4 6
2 6 0 3 5
3 7 1 0 2
1 5 5 4 0
Each number represents the shortest distance from the row node to the column node after applying the Floyd-Warshall algorithm.
Time Complexity
The algorithm runs in O(V³) time, where V is the number of vertices. This complexity arises from three nested loops, each iterating over all vertices.
Auxiliary Space
The space complexity is O(1) beyond the input distance matrix, as the algorithm updates the matrix in place without requiring additional significant storage.
Note
The above implementation of the Floyd-Warshall algorithm only computes and prints the shortest distances between all pairs of nodes.
If you want to also reconstruct and print the actual shortest paths, the algorithm can be modified by maintaining a predecessor matrix (or parent matrix). This separate 2D matrix stores the predecessor of each node on the shortest path, allowing you to trace back the path from the destination node to the source node.
Real-World Applications of the Floyd-Warshall Algorithm
1. Network Routing in Computer Networking
The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.
2. Flight Connectivity in Aviation
In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.
3. Geographic Information Systems (GIS)
GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.
4. Kleene’s Algorithm and Formal Language Theory
A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.
Network Routing in Computer Networking
The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.
Flight Connectivity in Aviation
In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.
Geographic Information Systems (GIS)
GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.
Kleene’s Algorithm and Formal Language Theory
A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Essentials of Machine Learning and Artificial Intelligence
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 22+ Hands-on Live Projects & Deployments
- Comprehensive Notes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 57% OFF
₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 60% OFF
₹15,000.00 ₹5,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085
