Data Structures and Algorithms
Menu

Heap Sort and Its Applications: A Comprehensive Guide

If you’re eager to master sorting algorithms and unlock career opportunities in tech, sign up for free course updates and expert resources to stay ahead. Understanding heap sort is a critical skill for coding interviews and real-world problem-solving—let’s dive in!

What is Heap Sort?

Heap sort, developed by J. W. J. Williams in 1964, is a comparison-based sorting algorithm that leverages the properties of a heap data structure to efficiently organize elements. Unlike simpler algorithms like bubble sort or insertion sort, heap sort guarantees a time complexity of O(n log n) in all scenarios, making it indispensable for large datasets.

Key Characteristics of Heap Sort

A heap is a complete binary tree where every parent node satisfies one of two conditions:

  • Max-Heap: Parent nodes are greater than or equal to their children.
  • Min-Heap: Parent nodes are smaller than or equal to their children.

Heap sort transforms an unsorted array into a heap structure, then repeatedly extracts the root (maximum or minimum value) to build a sorted array.

Why Use Heap Sort?

  • Predictable Performance: Unlike quicksort, which can degrade to O(n²) in worst-case scenarios, heap sort maintains O(n log n) time.
  • Memory Efficiency: It sorts in-place, requiring only O(1) auxiliary space.
  • Versatility: Used in priority queues, graph algorithms, and real-time systems.

Example of a Max-Heap:

       10  

       /  \  

      8    9  

     / \  /  

    5  6 7  

 

The root (10) is the largest element, and each parent is larger than its children.

How Does Heap Sort Work?

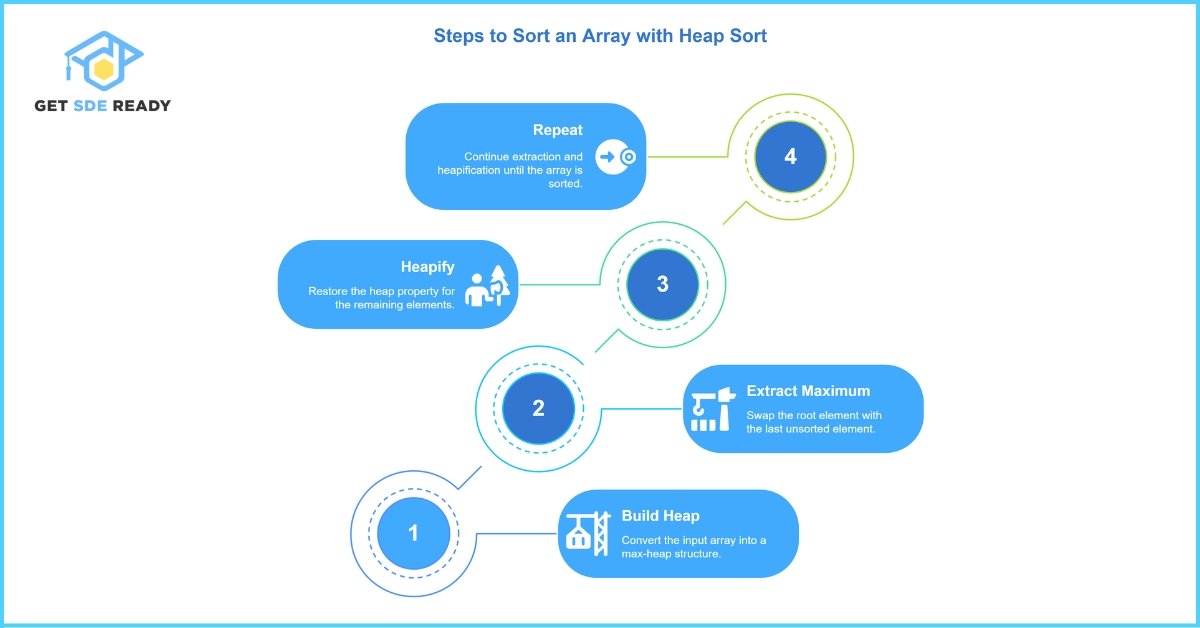
Step-by-Step Breakdown

  1. Build a Heap: Convert the input array into a max-heap.
  2. Extract Maximum: Swap the root (largest element) with the last unsorted element.
  3. Heapify: Restore the heap property for the remaining elements.

Repeat: Continue extraction and heapification until the array is sorted.

How Does Heap Sort Work

Detailed Example Walkthrough

Let’s sort [3, 1, 6, 5, 2, 4] step-by-step:

  1. Build Max-Heap:
    • Start with the initial array: [3, 1, 6, 5, 2, 4]

Convert to a max-heap:

    6  

  /   \  

 5     4  

/ \   /  

  •  

1 2 3

 – Array becomes `[6, 5, 4, 1, 2, 3]`.

  1.  
  2. Extract and Heapify:

     

    • Swap root (6) with last element (3): [3, 5, 4, 1, 2, 6]

Heapify the remaining [3, 5, 4, 1, 2] to restore max-heap:

    5  

  /   \  

 3     4  

/ \  

  •  

1 2

 – Repeat until sorted. Final array: `[1, 2, 3, 4, 5, 6]`.

Python Code Explained

				
					def heapify(arr, n, i):
    largest = i  # Initialize largest as root
    left = 2 * i + 1  # Left child index
    right = 2 * i + 2  # Right child index

    # Check if left child exists and is greater than root
    if left < n and arr[left] > arr[largest]:
        largest = left

    # Check if right child exists and is greater than current largest
    if right < n and arr[right] > arr[largest]:
        largest = right

    # Swap root if needed and recursively heapify affected subtree
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # Build max-heap (start from last non-leaf node)
    for i in range(n//2 - 1, -1, -1):
        heapify(arr, n, i)

    # Extract elements one by one
    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]  # Swap root with last element
        heapify(arr, i, 0)  # Heapify reduced heap

    return arr

Time and Space Complexity of Heap Sort

Detailed Analysis

Scenario

Time Complexity

Explanation

Best Case

O(n log n)

Even if the array is already a heap, extracting elements requires O(log n) per extraction.

Average Case

O(n log n)

Consistent performance regardless of input order.

Worst Case

O(n log n)

No degradation due to the structure of heap operations.

Space Complexity: O(1) – In-place sorting with minimal auxiliary space.

Benchmark Comparison

Algorithm

Best Case

Average Case

Worst Case

Stability

Heap Sort

O(n log n)

O(n log n)

O(n log n)

No

Quick Sort

O(n log n)

O(n log n)

O(n²)

No

Merge Sort

O(n log n)

O(n log n)

O(n log n)

Yes

Bubble Sort

O(n)

O(n²)

O(n²)

Yes

Why Heap Sort Isn’t Always the Default Choice:

  • Higher Constant Factors: Operations like heapification add overhead, making it slower than quicksort for small datasets.
  • Not Stable: Equal elements may not retain their original order, which matters in applications like database sorting.

     

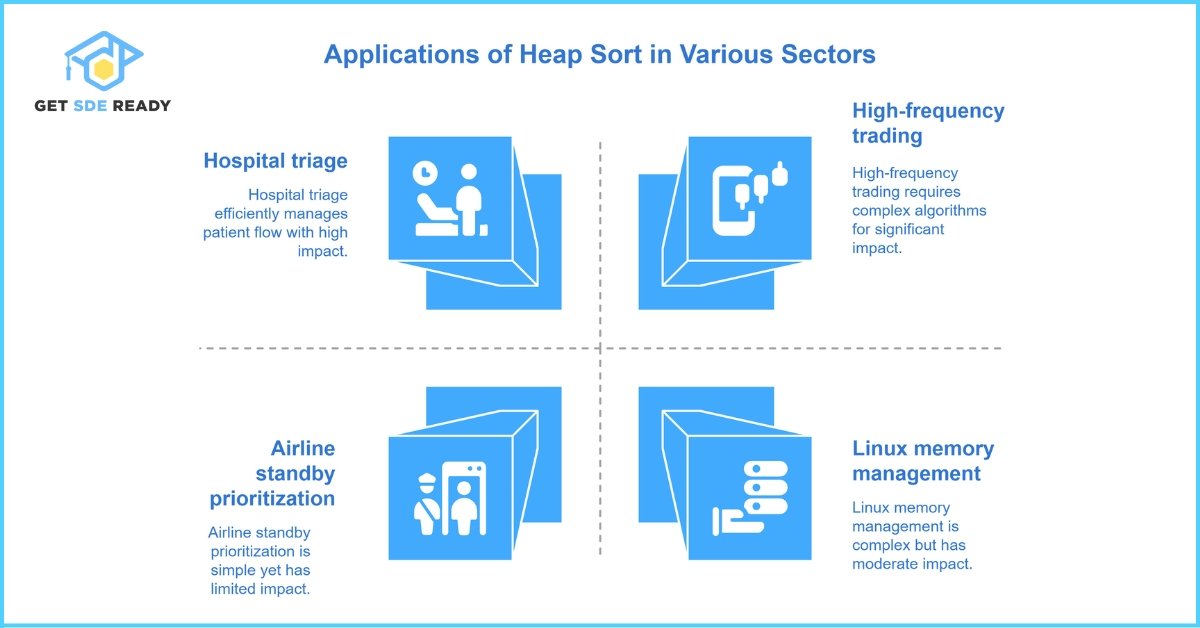
Applications of Heap Sort

Real-World Use Cases

  1. Priority Queues:
    • Hospitals use max-heaps to triage patients by severity.
    • Airlines prioritize standby passengers based on loyalty status.
  2. Graph Algorithms:
    • Dijkstra’s Shortest Path: Uses a priority queue (min-heap) to select the next node efficiently.
    • Prim’s Minimum Spanning Tree: Relies on heaps to pick the smallest edge weights.
  3. Operating Systems:
    • Memory Management: The Linux kernel uses heaps for dynamic memory allocation.
    • Job Scheduling: Real-time systems prioritize tasks using heap structures.
  4. Financial Systems:

     

    • High-frequency trading platforms process transactions in O(log n) time using heaps.

Industry-Specific Implementations

  • E-commerce: Amazon’s recommendation engine sorts products by user relevance using hybrid heap-based algorithms.
  • Gaming: Real-time leaderboards in multiplayer games update rankings efficiently with heaps.

Case Study

Netflix’s Content Delivery Network uses heap sort to manage server requests during peak traffic, ensuring low-latency streaming. For similar large-scale system design strategies, explore our Master DSA, Web Dev & System Design course.

Applications of Heap Sort

Advantages and Limitations of Heap Sort

Advantages

  • Guaranteed O(n log n) Performance: Ideal for time-critical applications like robotics.
  • Memory Efficiency: Critical for embedded systems (e.g., IoT devices).
  • No Worst-Case Degradation: Unlike quicksort, no risk of O(n²) time.

Limitations

  • Not Stable: Unsuitable for sorting databases where original order matters.
  • Slower for Small Datasets: Overhead of heap operations makes it less efficient than insertion sort for small n.

When to Use Heap Sort

  • Sorting large datasets (e.g., logs, financial transactions).
  • Applications requiring predictable performance (e.g., real-time systems).
Advantages and Limitations of Heap Sort

How does heap sort differ from quicksort in practice?

Heap sort’s O(n log n) guarantee makes it reliable for large data, but its higher constant factors make it slower than quicksort for smaller arrays. For mastering these trade-offs, our Data Structures & Algorithms Course includes hands-on comparisons.

Unlike merge sort, heap sort is inherently sequential due to dependencies in heapification. However, hybrid approaches (e.g., using multi-threaded heaps) are explored in advanced Data Science applications.

Swapping elements during heapification can disrupt the original order of equal keys. For stable sorting needs, learn alternative methods in our Design & DSA Combined Course that cover stability-preserving techniques.

Got Confusion ?

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Explore our flagship courses

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Get SDE Ready

Learning often happens in classrooms
but it doesn’t have to.

+91-9773728034
[email protected]
WhatsApp Icon
close menu icon

Master Your Interviews with Our Free Roadmap!

close menu icon

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

close menu icon

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design

close menu icon

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.