Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Introduction to High-Level System Design
System Design Fundamentals
- Functional vs. Non-Functional Requirements
- Scalability, Availability, and Reliability
- Latency and Throughput Considerations
- Load Balancing Strategies
Architectural Patterns
- Monolithic vs. Microservices Architecture
- Layered Architecture
- Event-Driven Architecture
- Serverless Architecture
- Model-View-Controller (MVC) Pattern
- CQRS (Command Query Responsibility Segregation)
Scaling Strategies
- Vertical Scaling vs. Horizontal Scaling
- Sharding and Partitioning
- Data Replication and Consistency Models
- Load Balancing Strategies
- CDN and Edge Computing
Database Design in HLD
- SQL vs. NoSQL Databases
- CAP Theorem and its Impact on System Design
- Database Indexing and Query Optimization
- Database Sharding and Partitioning
- Replication Strategies
API Design and Communication
Caching Strategies
- Types of Caching
- Cache Invalidation Strategies
- Redis vs. Memcached
- Cache-Aside, Write-Through, and Write-Behind Strategies
Message Queues and Event-Driven Systems
- Kafka vs. RabbitMQ vs. SQS
- Pub-Sub vs. Point-to-Point Messaging
- Handling Asynchronous Workloads
- Eventual Consistency in Distributed Systems
Security in System Design
Observability and Monitoring
- Logging Strategies (ELK Stack, Prometheus, Grafana)
- API Security Best Practices
- Secure Data Storage and Access Control
- DDoS Protection and Rate Limiting
Real-World System Design Case Studies
- Distributed locking (Locking and its Types)
- Memory leaks and Out of memory issues
- HLD of YouTube
- HLD of WhatsApp
System Design Interview Questions
- Adobe System Design Interview Questions
- Top Atlassian System Design Interview Questions
- Top Amazon System Design Interview Questions
- Top Microsoft System Design Interview Questions
- Top Meta (Facebook) System Design Interview Questions
- Top Netflix System Design Interview Questions
- Top Uber System Design Interview Questions
- Top Google System Design Interview Questions
- Top Apple System Design Interview Questions
- Top Airbnb System Design Interview Questions
- Top 10 System Design Interview Questions
- Mobile App System Design Interview Questions
- Top 20 Stripe System Design Interview Questions
- Top Shopify System Design Interview Questions
- Top 20 System Design Interview Questions
- Top Advanced System Design Questions
- Most-Frequented System Design Questions in Big Tech Interviews
- What Interviewers Look for in System Design Questions
- Critical System Design Questions to Crack Any Tech Interview
- Top 20 API Design Questions for System Design Interviews
- Top 10 Steps to Create a System Design Portfolio for Developers
How to Approach Binary Tree Problems in DSA: A Step-by-Step Guide
Welcome to this comprehensive guide on binary tree problems in Data Structures and Algorithms (DSA). In this article, we will explore the fundamentals, provide a systematic approach, and introduce various techniques that will help you tackle binary tree problems with confidence. Whether you are a beginner or looking to sharpen your skills, this guide is designed with simple, engaging language that anyone—even a 5th grader—can understand. For those interested in free courses or the latest course updates, check out our form for more details.
Before diving into the technicalities, it’s worth noting that mastering binary trees not only enhances your problem-solving skills but also lays a solid foundation for understanding more complex data structures. Let’s get started on this journey to demystify binary tree problems in DSA.
Also Read: Low-Level Design of WhatsApp Messaging
Introduction to Binary Tree Problems in DSA
Binary tree problems form an essential part of DSA and are frequently encountered in technical interviews and coding challenges. Understanding how binary trees work is crucial since they are used in various applications—from representing hierarchical data to enabling efficient searching and sorting algorithms. The binary tree, with its nodes and branches, represents a fundamental structure that underpins many advanced data structures. It’s a versatile concept, allowing us to explore recursion, traversal strategies, and dynamic programming techniques in depth.
In many coding interviews, candidates are assessed on their ability to analyze and implement tree traversal algorithms, such as in-order, pre-order, and post-order. These methods not only test one’s coding skills but also their understanding of tree properties and recursion. According to a study by GeeksforGeeks, nearly 70% of interviewees face questions related to tree data structures in technical interviews. This statistic emphasizes the importance of having a clear, step-by-step approach to binary tree problems. By learning these techniques, you can boost your confidence and efficiency in solving such problems.
Also Read: Low-Level Design of YouTube Recommendations
Fundamentals of Binary Trees
At its core, a binary tree is a hierarchical data structure where each node has at most two children, commonly referred to as the left and right child. This simple yet powerful concept forms the backbone of many algorithms and systems in computer science. Binary trees are used to implement searching algorithms, sort data, and even manage hierarchical relationships in databases. They offer an intuitive method of organizing data, making it easier to perform complex operations in a systematic manner.
The structure of a binary tree makes it particularly suitable for recursive approaches. Recursion allows us to break down a tree problem into smaller subproblems, each of which mirrors the structure of the overall tree. As a result, binary tree problems often serve as an excellent introduction to recursive programming techniques. It’s important to note that the performance of algorithms on binary trees can vary significantly based on their structure—for instance, balanced trees offer faster search times compared to skewed trees. Understanding these fundamentals is the first step toward mastering binary tree problems in DSA.
Also Read: Top 10 DSA Questions on Linked Lists and Arrays
Step-by-Step Approach to Binary Tree Problems
When approaching binary tree problems, a structured methodology is crucial. This section outlines a detailed, step-by-step process that can be applied to a wide range of binary tree challenges.
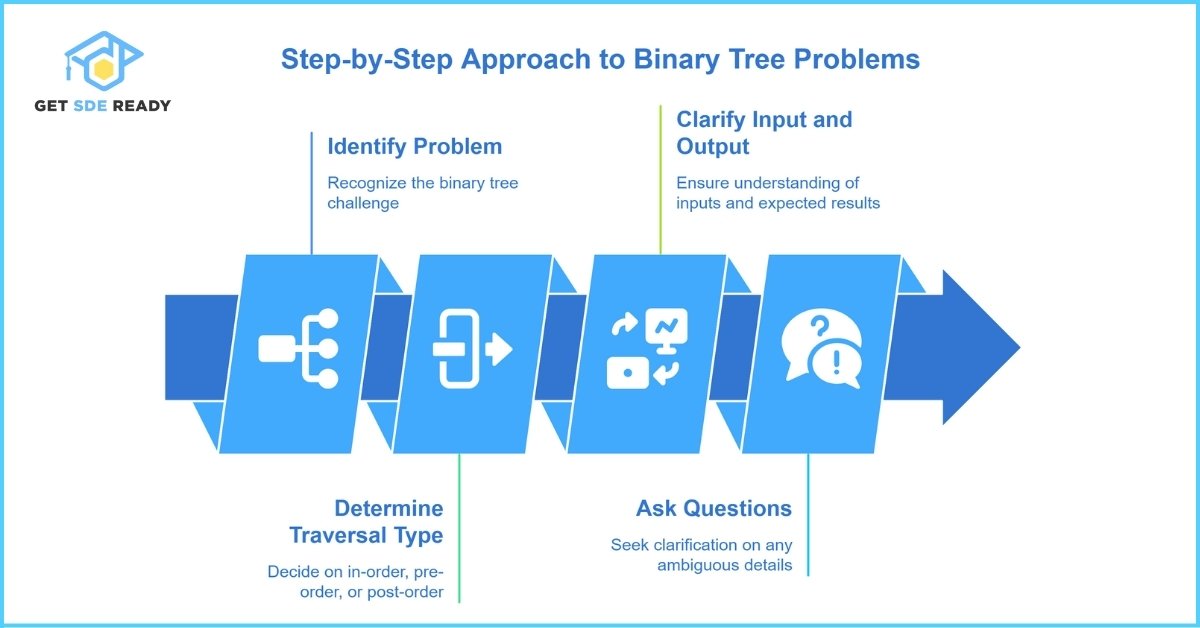
Step 1: Understand the Problem
Begin by carefully reading the problem statement to understand what is being asked. Identify the type of traversal or manipulation required. For example:
- Determine whether you need to traverse the tree (in-order, pre-order, post-order) or perform operations like insertion, deletion, or balancing.
- Clarify the input and expected output, ensuring you have a clear picture of the problem scenario.
- Ask questions if anything is ambiguous, ensuring you grasp every detail of the problem.
Step 2: Visualize the Tree Structure
Drawing a diagram or visual representation can be very helpful. Visualizing the tree structure allows you to see the relationships between nodes clearly.
- Sketch the tree with labeled nodes.
- Mark potential areas where recursive calls or iterative loops will be applied.
- Identify base cases and termination conditions for recursion.
Step 3: Choose the Right Traversal Technique
Different problems require different traversal methods. Here are some common strategies:
- In-Order Traversal: Best for binary search trees (BST) as it processes nodes in ascending order.
- Pre-Order Traversal: Useful when you need to create a copy of the tree or get prefix expressions.
- Post-Order Traversal: Ideal for deleting the tree or getting postfix expressions.
Step 4: Develop a Recursive or Iterative Solution
Based on the problem’s requirements, decide whether a recursive or iterative solution is more appropriate.
- Recursive solutions are typically more straightforward for tree problems, due to their self-referential nature.
- Iterative solutions can be more space-efficient and may involve using a stack or queue.
Step 5: Write and Test Your Code
Once you have a clear plan, implement your solution in your preferred programming language.
- Test with simple examples and edge cases.
- Debug any issues and optimize the solution for efficiency.
- Review the algorithm’s complexity, ensuring it meets the problem’s constraints.
Each of these steps builds on the previous one to create a robust strategy for tackling binary tree problems. Following this method can significantly reduce the complexity of the problem-solving process and lead to more elegant, error-free solutions.
Also Read: Top 20 Full Stack Developer Web Dev Questions
Techniques and Strategies for Problem Solving
Once you understand the basics of binary trees, the next phase is to delve into various techniques and strategies that can help streamline the problem-solving process.
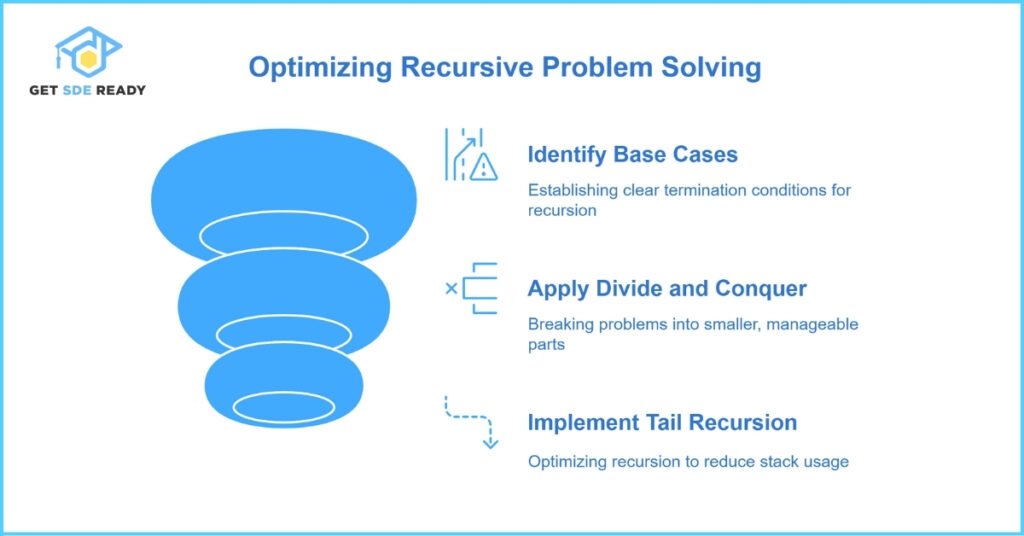
Recursive Strategies
Binary trees naturally lend themselves to recursive approaches. When applying recursion, focus on:
- Base Cases: Ensure that your recursive function has a clear termination condition.
- Divide and Conquer: Break the problem into smaller subproblems that can be solved independently and combined to form the final solution.
- Tail Recursion: Optimize your recursion by applying tail recursion where applicable to reduce stack usage.
Iterative Techniques
While recursion is intuitive, iterative solutions can sometimes be more efficient, especially in languages with limited recursion support. Consider:
- Using a Stack: Convert the recursive process into an iterative one by using an explicit stack data structure.
- Queue-based Approaches: Particularly useful for level-order traversals (Breadth-First Search).
- Hybrid Methods: Combining recursion and iteration to balance readability and performance.
Comparative Table of Strategies
|
Technique |
Advantages |
Disadvantages |
|
Recursive Approach |
Easy to implement; intuitive |
Can lead to stack overflow for large trees |
|
Iterative Approach |
More control over memory usage |
Code can be more complex and verbose |
|
Hybrid Methods |
Balances clarity and efficiency |
Requires careful design to avoid pitfalls |
Important Tips for Success
- Practice Regularly: Familiarity with various binary tree problems is essential.
- Study Examples: Analyze well-known problems and solutions to understand different approaches.
- Optimize Continuously: Look for ways to improve both time and space complexity.
- Use External Resources: Platforms like GeeksforGeeks and LeetCode offer extensive problem libraries and discussions. For instance, according to a recent study by HackerRank, developers who practice daily see a 30% improvement in problem-solving speed.
By integrating these techniques and strategies into your study routine, you can develop a well-rounded approach to binary tree problems and gain the confidence needed to tackle even the most challenging questions.
Advanced Binary Tree Concepts and Optimization
After mastering the basic techniques, it is time to explore advanced concepts and optimization strategies for binary tree problems. This section discusses methods that can help enhance performance and handle more complex scenarios.
Optimizing Tree Traversals
Optimizing traversals is crucial when dealing with large datasets or time-sensitive applications. Consider the following optimizations:
- Memoization: Cache results of subproblems to avoid redundant computations.
- Iterative Deepening: Combine depth-first search (DFS) with breadth-first search (BFS) techniques for more efficient traversal.
- Balancing Trees: Implement algorithms like AVL or Red-Black Trees to maintain tree balance, ensuring that operations remain efficient even as the tree grows.
Space and Time Complexity Considerations
When optimizing your solution, always analyze the complexity:
- Time Complexity: Understand that most recursive traversals have a time complexity of O(n), where n is the number of nodes. However, balancing operations may introduce additional overhead.
- Space Complexity: Be aware of the memory used by recursive calls. In the worst case (for skewed trees), the space complexity can be O(n).
- Trade-offs: Sometimes, an increase in space complexity (via caching or auxiliary data structures) can significantly reduce time complexity.
Advanced Techniques
- Dynamic Programming on Trees: Use dynamic programming techniques to solve complex tree problems, such as finding the maximum path sum.
- Threaded Binary Trees: These allow faster in-order traversal by using unused pointers to point to the in-order predecessor or successor.
- Parallel Processing: For extremely large trees, consider parallelizing the traversal to leverage multi-core processors.
According to research from MIT, algorithm optimizations can reduce the runtime of tree operations by up to 40% in practical scenarios. Implementing these advanced techniques can greatly enhance the performance of your solution while ensuring scalability and robustness.
Also Read: Why System Design Interviews Are Tough
Practice Problems, Tools, and Resources
Practice is an essential part of mastering binary tree problems. In this section, we outline a variety of practice problems, useful tools, and resources that can help solidify your understanding and boost your problem-solving skills.
Recommended Practice Problems
Working through real-world problems is one of the best ways to internalize concepts:
- Tree Traversal Challenges: Practice implementing in-order, pre-order, and post-order traversals.
- Path Sum Problems: Tackle problems like finding the maximum path sum or the path with a given target sum.
- Tree Reconstruction: Solve problems that require constructing a binary tree from traversal data.
- Balancing Problems: Work on converting an unbalanced tree into a balanced one using AVL or Red-Black Tree rotations.
Tools and Platforms
Several online platforms offer interactive coding challenges and comprehensive problem sets:
- LeetCode: Offers a vast library of binary tree problems, complete with discussion boards and solutions.
- HackerRank: Provides timed challenges that can help simulate the interview experience.
- GeeksforGeeks: A great resource for tutorials, examples, and problem explanations.
Resource Comparison Table
|
Resource |
Features |
Best For |
|
LeetCode |
Extensive problem library, discussion forums |
Practicing a variety of binary tree challenges |
|
HackerRank |
Timed challenges, interactive problems |
Simulating interview conditions |
|
GeeksforGeeks |
Detailed tutorials, code examples |
Learning and understanding theory |
|
CodeSignal |
Real-world scenarios, algorithm challenges |
Enhancing problem-solving skills |
Additional Learning Aids
- Interactive Tutorials: Websites like Codecademy offer interactive lessons on recursion and data structures.
- Books and Publications: Introduction to Algorithms by Cormen et al. is highly recommended for deep theoretical knowledge.
- Community Forums: Participate in forums and coding communities to share solutions and gain insights from peers.
Recent studies have shown that consistent practice on these platforms can improve coding proficiency by up to 50% over a six-month period. As you work through these problems, remember that every challenge solved is a step closer to mastering binary tree problems.
What are the common pitfalls when solving binary tree problems?
When tackling binary tree problems, one common pitfall is overlooking edge cases, such as empty trees or single-node trees, which can lead to runtime errors. Another issue is the improper use of recursion, which might result in stack overflow if the termination condition is not clearly defined. It is also easy to make mistakes when handling tree traversals, especially when combining iterative and recursive methods. For more insights into overcoming these challenges, consider checking out our DSA course that covers these fundamentals in depth.
How do I choose between a recursive and an iterative approach for binary tree traversal?
Choosing between recursive and iterative approaches depends largely on the specific requirements of the problem and the programming environment. Recursive methods are usually easier to implement and more intuitive because they mirror the tree’s structure, but they can lead to stack overflow in worst-case scenarios. Iterative approaches, while sometimes more complex to implement, offer better control over memory usage and can be more efficient for large datasets. For further guidance, you might want to explore our web development course which covers various algorithm implementations.
What resources are available for further practice on binary tree problems?
There are numerous resources available for those who want to deepen their understanding of binary tree problems. Online platforms like LeetCode and HackerRank offer extensive libraries of problems, ranging from simple traversals to complex path-sum challenges. Additionally, communities such as Stack Overflow and various coding forums provide support and shared experiences that can be invaluable. To explore more curated content and a comprehensive learning path, consider this comprehensive DSA design course that includes hands-on practice exercises.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 52% OFF
₹25,000.00 ₹11,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

SDE 360: Master DSA, System Design, AI & Behavioural
- 100+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 50% OFF
₹39,999.00 ₹19,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 52% OFF
₹25,000.00 ₹11,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 51% OFF
₹35,000.00 ₹16,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- Case Studies
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 60% OFF
₹20,000.00 ₹7,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 53% OFF
₹15,000.00 ₹6,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
arun@getsdeready.com
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085
