Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Introduction to High-Level System Design
System Design Fundamentals
- Functional vs. Non-Functional Requirements
- Scalability, Availability, and Reliability
- Latency and Throughput Considerations
- Load Balancing Strategies
Architectural Patterns
- Monolithic vs. Microservices Architecture
- Layered Architecture
- Event-Driven Architecture
- Serverless Architecture
- Model-View-Controller (MVC) Pattern
- CQRS (Command Query Responsibility Segregation)
Scaling Strategies
- Vertical Scaling vs. Horizontal Scaling
- Sharding and Partitioning
- Data Replication and Consistency Models
- Load Balancing Strategies
- CDN and Edge Computing
Database Design in HLD
- SQL vs. NoSQL Databases
- CAP Theorem and its Impact on System Design
- Database Indexing and Query Optimization
- Database Sharding and Partitioning
- Replication Strategies
API Design and Communication
Caching Strategies
- Types of Caching
- Cache Invalidation Strategies
- Redis vs. Memcached
- Cache-Aside, Write-Through, and Write-Behind Strategies
Message Queues and Event-Driven Systems
- Kafka vs. RabbitMQ vs. SQS
- Pub-Sub vs. Point-to-Point Messaging
- Handling Asynchronous Workloads
- Eventual Consistency in Distributed Systems
Security in System Design
Observability and Monitoring
- Logging Strategies (ELK Stack, Prometheus, Grafana)
- API Security Best Practices
- Secure Data Storage and Access Control
- DDoS Protection and Rate Limiting
Real-World System Design Case Studies
- Distributed locking (Locking and its Types)
- Memory leaks and Out of memory issues
- HLD of YouTube
- HLD of WhatsApp
System Design Interview Questions
- Adobe System Design Interview Questions
- Top Atlassian System Design Interview Questions
- Top Amazon System Design Interview Questions
- Top Microsoft System Design Interview Questions
- Top Meta (Facebook) System Design Interview Questions
- Top Netflix System Design Interview Questions
- Top Uber System Design Interview Questions
- Top Google System Design Interview Questions
- Top Apple System Design Interview Questions
- Top Airbnb System Design Interview Questions
- Top 10 System Design Interview Questions
- Mobile App System Design Interview Questions
- Top 20 Stripe System Design Interview Questions
- Top Shopify System Design Interview Questions
- Top 20 System Design Interview Questions
- Top Advanced System Design Questions
- Most-Frequented System Design Questions in Big Tech Interviews
- What Interviewers Look for in System Design Questions
- Critical System Design Questions to Crack Any Tech Interview
- Top 20 API Design Questions for System Design Interviews
- Top 10 Steps to Create a System Design Portfolio for Developers
How to Detect a Cycle in an Undirected Graph
Introduction
In graph theory, identifying cycles is a common and crucial task. A cycle in an undirected graph occurs when a path starts and ends at the same vertex without retracing any edge. This tutorial explains how to determine whether a given undirected graph contains a cycle.
Problem Statement
Given an undirected graph defined by a number of vertices V and a list of edges, the goal is to check for the presence of any cycle in the graph.
Example 1
Input:
V = 4
edges = [[0, 1], [0, 2], [1, 2], [2, 3]]
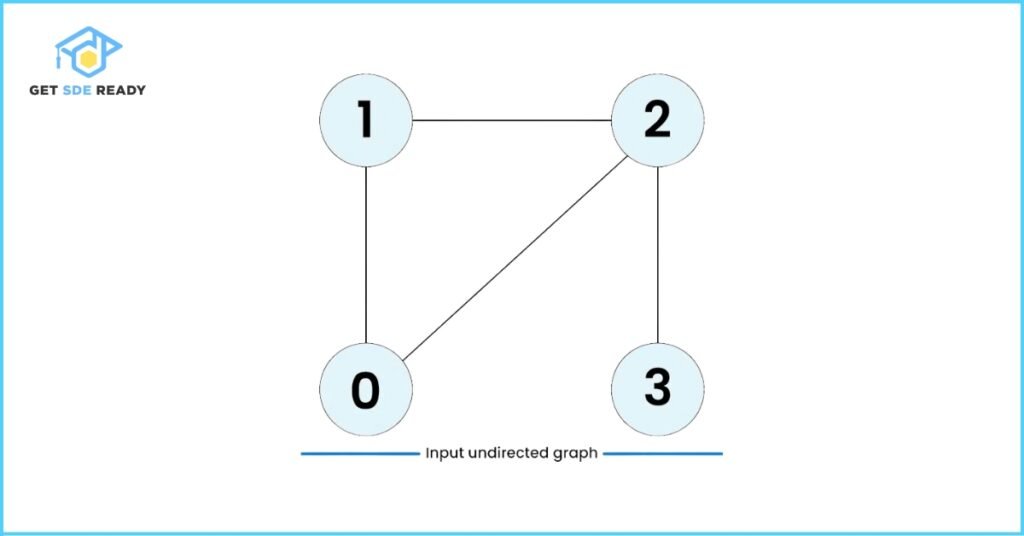
Output:
true
Explanation:
The connections in the graph form a cycle:
0 → 2 → 1 → 0.
This closed loop indicates the presence of a cycle.
Example 2
Input:
V = 4
edges = [[0, 1], [1, 2], [2, 3]]
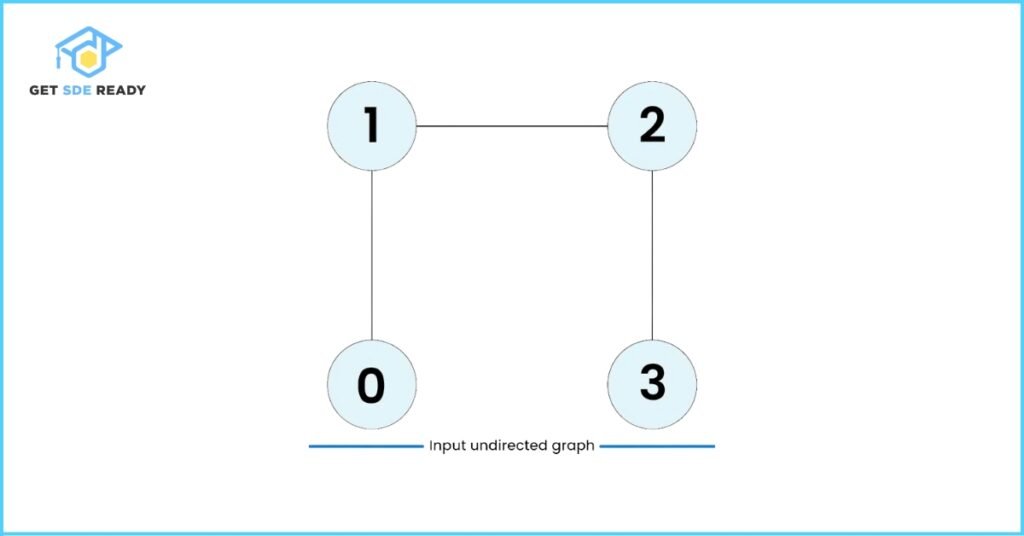
Output:
false
Explanation:
This graph represents a straight path without any repeated vertices or edges, so no cycle is formed.
Consider our Master DSA, Web Dev & System Design program for end-to-end learning.
Detect Cycle in an Undirected Graph Using BFS and DFS
Using Breadth-First Search (BFS) — Time: O(V + E), Space: O(V)
Breadth-First Search is a powerful technique for detecting cycles in an undirected graph. By exploring nodes level by level, BFS ensures the shortest path to each vertex and provides a reliable method to uncover cycles using minimal memory.
In this approach, we utilize:
- A visited array to keep track of visited vertices.
- A queue to perform level-order traversal.
During traversal:
- Each node is dequeued and its unvisited neighbors are enqueued.
- If we come across a node that is already visited and not the immediate parent, this indicates a cycle, as the node is accessible through multiple paths.
This level-wise traversal prevents redundant recursive calls and is particularly beneficial in handling large graphs more efficiently than DFS.
Note: You can refer to the complete implementation guide here: Detect Cycle in an Undirected Graph using BFS.
Using Depth-First Search (DFS) — Time: O(V + E), Space: O(V)
Depth-First Search is another effective method to detect cycles in undirected graphs. It explores as far as possible along each branch before backtracking, which can help reveal cycles in deeper layers of the graph.
However, unlike BFS, DFS requires an additional check:
- Since the graph is undirected, an edge from u to v is also from v to u.
- To prevent falsely detecting a cycle, we track the parent node during traversal.
- A cycle exists only if a visited neighbor is not the parent of the current node.
Steps to Implement the DFS Approach:
- Iterate through all nodes in the graph.
- Maintain a visited[] array to mark visited vertices.
- For every unvisited node, initiate a DFS call with its parent set to -1.
- Inside DFS:
- Mark the current node as visited.
- Traverse all adjacent nodes:
- If a neighbor is unvisited, recursively apply DFS on it.
- If a neighbor is already visited and not the parent, a cycle is detected.
5. If no such condition is met during traversal, return false.
This strategy ensures accurate cycle detection in undirected graphs while maintaining optimal time and space complexity.
DFS-Based Cycle Detection: Code Implementation
Below is the implementation of the DFS approach for cycle detection in an undirected graph.
// A C++ Program to detect cycle in an undirected graph
#include <bits/stdc++.h>
using namespace std;
bool isCycleUtil(int v, vector<vector<int>> &adj, vector<bool> &visited, int parent)
{
// Mark the current node as visited
visited[v] = true;
// Recur for all the vertices adjacent to this vertex
for (int i : adj[v])
{
// If an adjacent vertex is not visited, then recur for that adjacent
if (!visited[i])
{
if (isCycleUtil(i, adj, visited, v))
return true;
}
// If an adjacent vertex is visited and is not parent of current vertex,
// then there exists a cycle in the graph.
else if (i != parent)
return true;
}
return false;
}
vector<vector<int>> constructadj(int V, vector<vector<int>> &edges){
vector<vector<int>> adj(V);
for (auto it : edges)
{
adj[it[0]].push_back(it[1]);
adj[it[1]].push_back(it[0]);
}
return adj;
}
// Returns true if the graph contains a cycle, else false.
bool isCycle(int V, vector<vector<int>> &edges)
{
vector<vector<int>> adj = constructadj(V,edges);
// Mark all the vertices as not visited
vector<bool> visited(V, false);
for (int u = 0; u < V; u++)
{
if (!visited[u])
{
if (isCycleUtil(u, adj, visited, -1))
return true;
}
}
return false;
}
int main()
{
int V = 5;
vector<vector<int>> edges = {{0, 1}, {0, 2}, {0, 3}, {1, 2}, {3, 4}};
if (isCycle(V, edges))
{
cout << "true" << endl;
}
else
{
cout << "false" << endl;
}
return 0;
}
import java.util.*;
{
// Helper function to check cycle using DFS
static boolean isCycleUtil(int v, List<Integer>[] adj,
boolean[] visited,
int parent)
{
visited[v] = true;
// If an adjacent vertex is not visited,
// then recur for that adjacent
for (int i : adj[v]) {
if (!visited[i]) {
if (isCycleUtil(i, adj, visited, v))
return true;
}
// If an adjacent vertex is visited and
// is not parent of current vertex,
// then there exists a cycle in the graph.
else if (i != parent) {
return true;
}
}
return false;
}
static List<Integer>[] constructadj(int V, int [][] edges){
List<Integer>[] adj = new ArrayList[V];
for (int i = 0; i < V; i++) {
adj[i] = new ArrayList<>();
}
return adj;
}
// Function to check if graph contains a cycle
static boolean isCycle(int V, int[][] edges)
{
List<Integer> [] adj = constructadj(V,edges);
for (int[] edge : edges) {
adj[edge[0]].add(edge[1]);
adj[edge[1]].add(edge[0]);
}
boolean[] visited = new boolean[V];
// Call the recursive helper function
// to detect cycle in different DFS trees
for (int u = 0; u < V; u++) {
if (!visited[u]) {
if (isCycleUtil(u, adj, visited, -1))
return true;
}
}
return false;
}
public static void main(String[] args)
{
int V = 5;
int[][] edges = {
{0, 1}, {0, 2}, {0, 3}, {1, 2}, {3, 4}
};
if (isCycle(V, edges)) {
System.out.println("true");
}
else {
System.out.println("false");
}
}
}
// Helper function to check cycle using DFS
function isCycleUtil(v, adj, visited, parent)
{
visited[v] = true;
for (let i of adj[v]) {
if (!visited[i]) {
if (isCycleUtil(i, adj, visited, v)) {
return true;
}
}
else if (i !== parent) {
return true;
}
}
return false;
}
function constructadj(V, edges){
let adj = Array.from({length : V}, () => []);
// Build the adjacency list
for (let edge of edges) {
let [u, v] = edge;
adj[u].push(v);
adj[v].push(u);
}
return adj;
}
// Function to check if graph contains a cycle
function isCycle(V, edges)
{
let adj = constructadj(V,edges);
let visited = new Array(V).fill(false);
// Check each node
for (let u = 0; u < V; u++) {
if (!visited[u]) {
if (isCycleUtil(u, adj, visited, -1)) {
return true;
}
}
}
return false;
}
// Driver Code
const V = 5;
const edges =
[[0, 1], [0, 2], [0, 3], [1, 2], [3, 4]];
if (isCycle(V, edges)) {
console.log("true");
}
else {
console.log("false");
}
# Helper function to check cycle using DFS
def isCycleUtil(v, adj, visited, parent):
visited[v] = True
for i in adj[v]:
if not visited[i]:
if isCycleUtil(i, adj, visited, v):
return True
elif i != parent:
return True
return False
def constructadj(V, edges):
adj = [[] for _ in range(V)] # Initialize adjacency list
for edge in edges:
u, v = edge
adj[u].append(v)
adj[v].append(u)
return adj
# Function to check if graph contains a cycle
def isCycle(V, edges):
adj = constructadj(V,edges)
visited = [False] * V
for u in range(V):
if not visited[u]:
if isCycleUtil(u, adj, visited, -1):
return True
return False
# Driver Code
if __name__ == "__main__":
V = 5
edges = [(0, 1), (0, 2), (0, 3), (1, 2), (3, 4)]
if isCycle(V, edges):
print("true")
else:
print("false")
Output
true
Time Complexity:
O(V + E) — The DFS algorithm visits every vertex once (O(V)) and explores each edge exactly once (O(E)).
Auxiliary Space:
O(V) — Space is required for the visited array and the recursive call stack during DFS traversal.
Note: The adjacency list is not included in the auxiliary space calculation, as it is part of the input representation of the graph.
For deeper insights, explore our comprehensive Master DSA, Web Dev & System Design program.
FAQs
What distinguishes cycle detection in undirected vs. directed graphs?
In undirected graphs, a back-edge to any visited node that isn’t the immediate parent indicates a cycle. In directed graphs, cycle detection often uses DFS with recursion stack tracking or Kahn’s algorithm (topological sort) to spot back-edges respecting edge direction.
Can I use BFS instead of DFS for cycle detection?
Yes. BFS tracks parent nodes similarly: when encountering a visited neighbor that is not the parent during level-order traversal, a cycle is detected. BFS may be preferable when you also need shortest-path information.
How do I handle disconnected graphs?
Iterate through all vertices; for each unvisited vertex, initiate BFS or DFS. This ensures each connected component is checked for cycles independently.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Essentials of Machine Learning and Artificial Intelligence
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 22+ Hands-on Live Projects & Deployments
- Comprehensive Notes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 57% OFF
₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 60% OFF
₹15,000.00 ₹5,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085
