Data Structures and Algorithms

DSA Interview Questions

Introduction to Disjoint Set (Union-Find Algorithm)

Disjoint sets are collections in which no element is shared between any two sets. The Disjoint Set data structure, also known as the Union-Find algorithm, is designed to manage such sets efficiently. It primarily supports the following operations:

Union Operation: Combines two distinct disjoint sets into one.
Find Operation: Identifies the representative (or root) of the set an element belongs to.
Set Membership Check: Determines if two elements are part of the same set by comparing their representatives.

Scenario: Friendship Connections

Imagine a scenario involving several individuals, where you need to carry out the following tasks:

Establish a New Friendship

When person x becomes friends with person y, this effectively adds a new connection within a set.

Verify a Friendship Link

Check if person x is connected—directly or indirectly—to person y, meaning they belong to the same set.

Examples

Suppose we have a group of 10 individuals labeled: a, b, c, d, e, f, g, h, i, j.
We are given the following friendship connections to establish:

a ↔ b
b ↔ d
c ↔ f
c ↔ i
j ↔ e
g ↔ j

Now, if we are asked queries such as “Is a a friend of d?”, the goal is to determine whether two people belong to the same group (either directly or through mutual friends). After applying the union operations for the given relationships, the individuals are organized into the following four disjoint sets (groups):

G1 = {a, b, d}
G2 = {c, f, i}
G3 = {e, g, j}
G4 = {h}

These groups represent clusters of connected friends, and the Disjoint Set (Union-Find) structure allows quick checks for whether any two individuals belong to the same group.

For a comprehensive foundation in DSA, including Disjoint Set, consider exploring our DSA course which covers these basics and more.

Determining If Two Individuals Belong to the Same Group

To check whether two individuals x and y are part of the same group (i.e., whether they are directly or indirectly connected as friends), we use a technique known as Disjoint Set Union (DSU). This approach organizes individuals into distinct sets, each represented by one of its members, and efficiently manages these groupings.

Key Concepts to Understand

Set Initialization and Resolution

At the beginning, every individual belongs to a separate set. As relationships are processed, we unify the corresponding sets by choosing a single element to act as the representative of the set.

Group Membership Check

To verify if two individuals are in the same group, we compare the representatives of their respective sets. If both share the same representative, they are part of the same group and are therefore friends.

Data Structures Used

Array (Parent[])

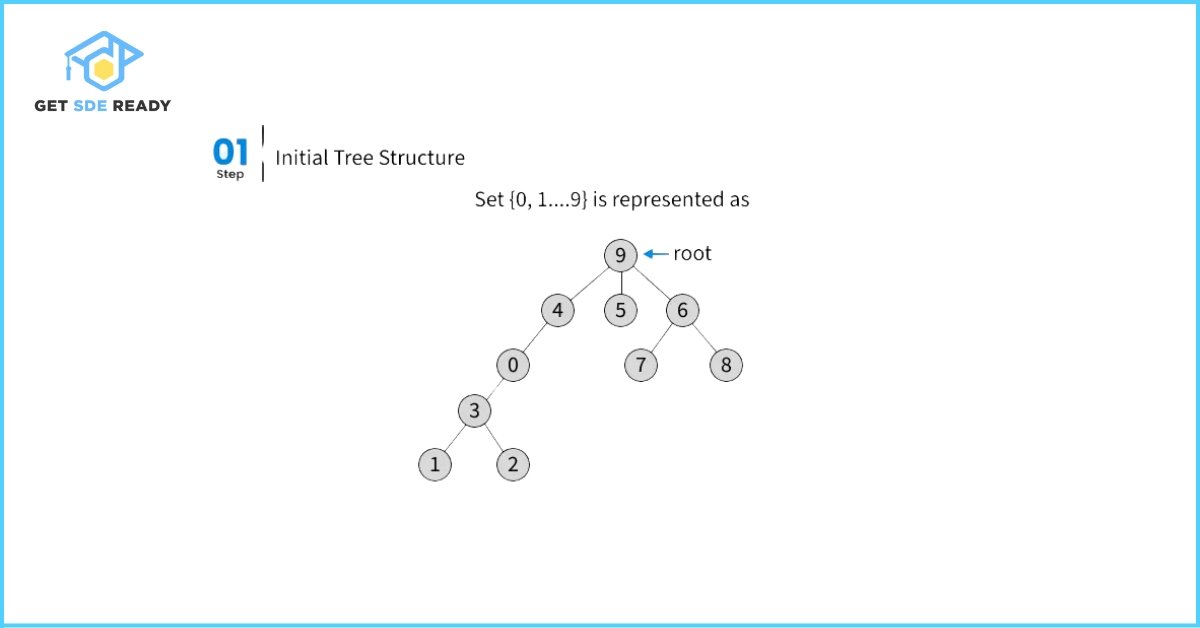
This array keeps track of parent relationships. For N individuals, the i-th index of the Parent[] array indicates the parent of the i-th item. This structure forms a virtual forest of trees.

Tree Structure

Each disjoint set is represented as a tree. If two individuals are part of the same tree, they belong to the same set. The root node of the tree acts as the representative of that set. A simple rule applies:
- If i is the representative, then Parent[i] = i.
- If i is not the representative, traverse upward through the parent pointers until the root (representative) is found.

Core Operations in Disjoint Set

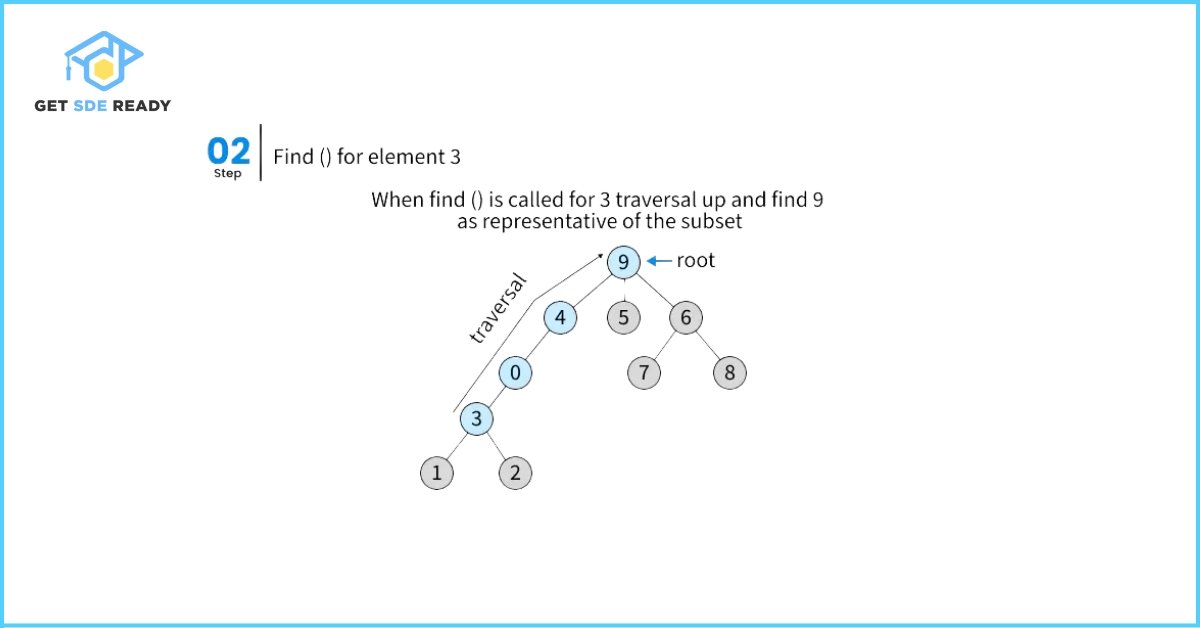
Find Operation

This operation retrieves the representative of the set to which a given element belongs. It works by recursively navigating the Parent[] array until it reaches a node that is its own parent—indicating the root of the tree.

Union Operation

This combines two distinct sets into one. It takes two elements, finds their respective representatives using the Find operation, and then connects one tree under the root of the other, effectively merging the sets.

For hands-on implementation and practice problems on these optimizations, check our Union-Find deep dive in the Crash Course.

Code Examples

Below are naive implementations in various languages:

BFS Traversal Output:

				
					#include <iostream>
#include <vector>
using namespace std;

class UnionFind {
    vector<int> parent;
public:
    UnionFind(int size) {
        parent.resize(size);
        // Initialize the parent array with each element as its own representative
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    // Find the representative (root) of the set that includes element i
    int find(int i) {
        // If i itself is root or representative
        if (parent[i] == i) {
            return i;
        }
        // Else recursively find the representative of the parent
        return find(parent[i]);
    }

    // Unite (merge) the set that includes element i and the set that includes element j
    void unite(int i, int j) {
        int irep = find(i);
        int jrep = find(j);
        parent[irep] = jrep;
    }
};

int main() {
    int size = 5;
    UnionFind uf(size);
    uf.unite(1, 2);
    uf.unite(3, 4);
    bool inSameSet = (uf.find(1) == uf.find(2));
    cout << "Are 1 and 2 in the same set? " 
         << (inSameSet ? "Yes" : "No") << endl;
    return 0;
}

				
					import java.util.Arrays;

public class UnionFind {
    private int[] parent;

    public UnionFind(int size) {
        parent = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    // Find the representative (root) of the set that includes element i
    public int find(int i) {
        if (parent[i] == i) {
            return i;
        }
        return find(parent[i]);
    }

    // Unite (merge) the set that includes element i and the set that includes element j
    public void union(int i, int j) {
        int irep = find(i);
        int jrep = find(j);
        parent[irep] = jrep;
    }

    public static void main(String[] args) {
        int size = 5;
        UnionFind uf = new UnionFind(size);
        uf.union(1, 2);
        uf.union(3, 4);
        boolean inSameSet = uf.find(1) == uf.find(2);
        System.out.println("Are 1 and 2 in the same set? " + inSameSet);
    }
}

				
					class UnionFind {
    constructor(size) {
        this.parent = Array.from({ length: size }, (_, i) => i);
    }

    find(i) {
        if (this.parent[i] === i) {
            return i;
        }
        return this.find(this.parent[i]);
    }

    unite(i, j) {
        const irep = this.find(i);
        const jrep = this.find(j);
        this.parent[irep] = jrep;
    }
}

// Example usage
const size = 5;
const uf = new UnionFind(size);
uf.unite(1, 2);
uf.unite(3, 4);
const inSameSet = uf.find(1) === uf.find(2);
console.log("Are 1 and 2 in the same set?", inSameSet ? "Yes" : "No");

				
					# Function to find BFS of Graph from given source s
def bfs(adj):
    
    # get number of vertices
    V = len(adj)
    
    # create an array to store the traversal
    res = []
    s = 0
    # Create a queue for BFS
    from collections import deque
    q = deque()
    
    # Initially mark all the vertices as not visited
    visited = [False] * V
    
    # Mark source node as visited and enqueue it
    visited[s] = True
    q.append(s)
    
    # Iterate over the queue
    while q:
        
        # Dequeue a vertex from queue and store it
        curr = q.popleft()
        res.append(curr)
        
        # Get all adjacent vertices of the dequeued 
        # vertex curr If an adjacent has not been 
        # visited, mark it visited and enqueue it
        for x in adj[curr]:
            if not visited[x]:
                visited[x] = True
                q.append(x)
                
    return res

if __name__ == "__main__":
    
    # create the adjacency list
    # [ [2, 3, 1], [0], [0, 4], [0], [2] ]
    adj = [[1,2], [0,2,3], [0,4], [1,4], [2,3]]
    ans = bfs(adj)
    for i in ans:
        print(i, end=" ")

Output

0 1 2 3 4

BFS in a Disconnected Graph

The standard Breadth-First Search (BFS) implementation starts from a given source node and explores only the vertices that are reachable from that source. However, if the graph is disconnected, this method won’t visit all vertices—some components may remain unexplored.

To handle such cases, we need a modified approach that ensures complete traversal, even when the graph contains disconnected components.

				
					#include<bits/stdc++.h>
using namespace std;

// BFS from given source s
void bfs(vector<vector<int>>& adj, int s, 
        vector<bool>& visited, vector<int> &res) {

    // Create a queue for BFS
    queue<int> q; 

    // Mark source node as visited and enqueue it
    visited[s] = true;
    q.push(s);

    // Iterate over the queue
    while (!q.empty()) {

        // Dequeue a vertex and store it
        int curr = q.front(); 
        q.pop();
        res.push_back(curr);

        // Get all adjacent vertices of the dequeued 
        // vertex curr If an adjacent has not been 
        // visited, mark it visited and enqueue it
        for (int x : adj[curr]) {
            if (!visited[x]) {
                visited[x] = true;
                q.push(x);
            }
        }
    }
}
                      
// Perform BFS for the entire graph which maybe
// disconnected
vector<int> bfsDisconnected(vector<vector<int>>& adj) {
    int V = adj.size();

    // create an array to store the traversal
    vector<int> res;

    // Initially mark all the vertices as not visited
    vector<bool> visited(V, false); 

    // perform BFS for each node
    for (int i = 0; i < adj.size(); ++i) {
        if (!visited[i]) {
            bfs(adj, i, visited, res);
        }
    }

    return res;
}

int main()  {

    vector<vector<int>> adj = { {1, 2}, {0}, {0},
                                {4}, {3, 5}, {4}};
    vector<int> ans = bfsDisconnected(adj);
    for(auto i:ans) {
        cout<<i<<" ";
    }
    return 0;
}

				
					// BFS from given source s
import java.util.*;

class GfG {

    // BFS from given source s
    static ArrayList<Integer> 
        bfsOfGraph(ArrayList<ArrayList<Integer>> adj, 
                int s, boolean[] visited, ArrayList<Integer> res) {

        // Create a queue for BFS
        Queue<Integer> q = new LinkedList<>();

        // Mark source node as visited and enqueue it
        visited[s] = true;
        q.add(s);

        // Iterate over the queue
        while (!q.isEmpty()) {

            // Dequeue a vertex and store it
            int curr = q.poll();
            res.add(curr);

            // Get all adjacent vertices of the dequeued 
            // vertex curr If an adjacent has not been 
            // visited, mark it visited and enqueue it
            for (int x : adj.get(curr)) {
                if (!visited[x]) {
                    visited[x] = true;
                    q.add(x);
                }
            }
        }
        return res;
    }

    // Perform BFS for the entire graph which maybe
    // disconnected
    static ArrayList<Integer> bfsDisconnected(
                ArrayList<ArrayList<Integer>> adj) {
        int V = adj.size();

        // create an array to store the traversal
        ArrayList<Integer> res = new ArrayList<>();

        // Initially mark all the vertices as not visited
        boolean[] visited = new boolean[V];

        // perform BFS for each node
        for (int i = 0; i < V; i++) {
            if (!visited[i]) {
                bfsOfGraph(adj, i, visited, res);
            }
        }
        return res;
    }

    public static void main(String[] args) {
        ArrayList<ArrayList<Integer>> adj = new ArrayList<>();
        adj.add(new ArrayList<>(Arrays.asList(1, 2)));
        adj.add(new ArrayList<>(Arrays.asList(0))); 
        adj.add(new ArrayList<>(Arrays.asList(0)));   
        adj.add(new ArrayList<>(Arrays.asList(4)));
        adj.add(new ArrayList<>(Arrays.asList(3, 5)));
        adj.add(new ArrayList<>(Arrays.asList(4)));  

        int src = 0;
        ArrayList<Integer> ans = bfsDisconnected(adj);
        for (int i : ans) {
            System.out.print(i + " ");
        }
    }
}

				
					// BFS from given source s
function bfsOfGraph(adj, s, visited, res) {
    
    // Create a queue for BFS
    let q = [];
    
    // Mark source node as visited and enqueue it
    visited[s] = true;
    q.push(s);
    
    // Iterate over the queue
    while (q.length > 0) {
        
        // Dequeue a vertex and store it
        let curr = q.shift();
        res.push(curr);
        
        // Get all adjacent vertices of the dequeued 
        // vertex curr If an adjacent has not been 
        // visited, mark it visited and enqueue it
        for (let x of adj[curr]) {
            if (!visited[x]) {
                visited[x] = true;
                q.push(x);
            }
        }
    }
    return res;
}
 
// Perform BFS for the entire graph which maybe
// disconnected
function bfsDisconnected(adj) {
    let V = adj.length;
    
    // create an array to store the traversal
    let res = [];
    
    // Initially mark all the vertices as not visited
    let visited = new Array(V).fill(false);
    
    // perform BFS for each node
    for (let i = 0; i < V; i++) {
        if (!visited[i]) {
            bfsOfGraph(adj, i, visited, res);
        }
    }
    return res;
}
 
// Main execution
let adj =
    [[1, 2], [0], [0],
    [4], [3, 5], [4]];
let ans = bfsDisconnected(adj);
for (let i of ans) {
    process.stdout.write(i + " ");
}

				
					# BFS from given source s
from collections import deque

def bfsOfGraph(adj, s, visited, res):
    
    # Create a queue for BFS
    q = deque()
    
    # Mark source node as visited and enqueue it
    visited[s] = True
    q.append(s)
    
    # Iterate over the queue
    while q:
        
        # Dequeue a vertex and store it
        curr = q.popleft()
        res.append(curr)
        
        # Get all adjacent vertices of the dequeued 
        # vertex curr If an adjacent has not been 
        # visited, mark it visited and enqueue it
        for x in adj[curr]:
            if not visited[x]:
                visited[x] = True
                q.append(x)
    return res

# Perform BFS for the entire graph which maybe
# disconnected
def bfsDisconnected(adj):
    V = len(adj)
    
    # create an array to store the traversal
    res = []
    
    # Initially mark all the vertices as not visited
    visited = [False] * V
    
    # perform BFS for each node
    for i in range(V):
        if not visited[i]:
            bfsOfGraph(adj, i, visited, res)
    return res

if __name__ == "__main__":
    adj = [[1, 2], [0], [0],
        [4], [3, 5], [4]]
    ans = bfsDisconnected(adj)
    for i in ans:
        print(i, end=" ")

Output

0 1 2 3 4

BFS in a Disconnected Graph

To handle such cases, we need a modified approach that ensures complete traversal, even when the graph contains disconnected components.

Network Routing in Computer Networking

The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.

Flight Connectivity in Aviation

In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.

Geographic Information Systems (GIS)

GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.

Kleene’s Algorithm and Formal Language Theory

A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.

Output Example

Are 1 and 2 in the same set? → Yes

This indicates that elements 1 and 2 belong to the same disjoint set, either directly or through a chain of connections.

However, the basic implementations of union() and find() shown above are naive, and in the worst-case scenario, their time complexity can grow linearly. The tree structures formed to represent subsets can become highly unbalanced, resembling a linked list rather than a tree. This leads to inefficient traversals during the find() operation.

Here’s an illustration of such a worst-case scenario where all nodes end up chained in a single line, resulting in slow performance.

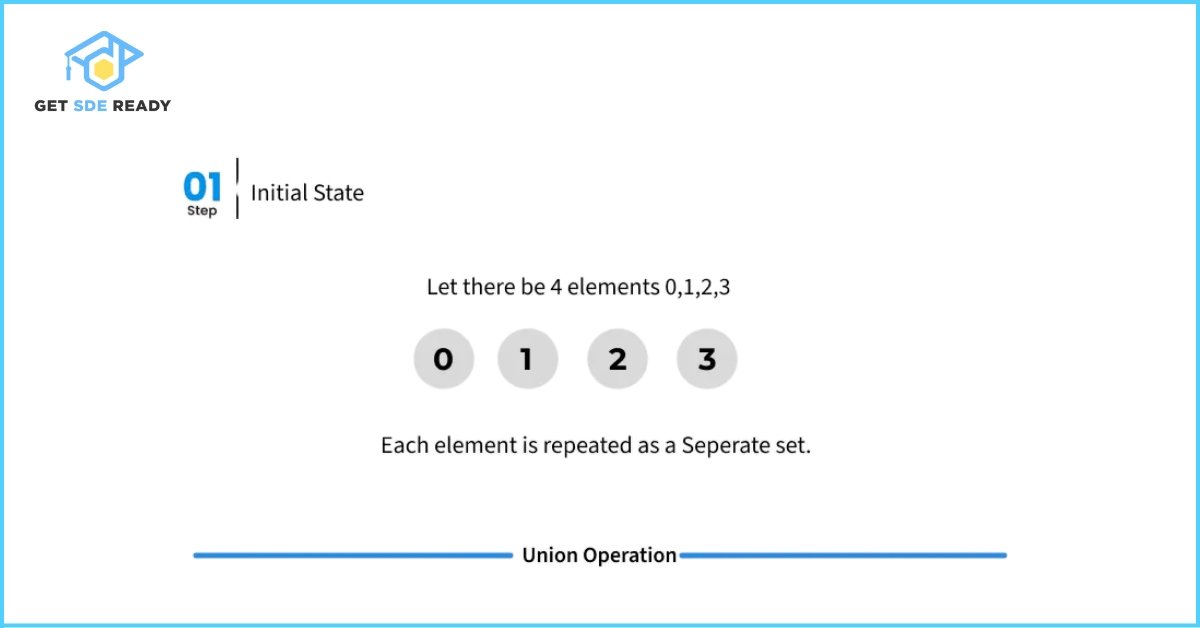
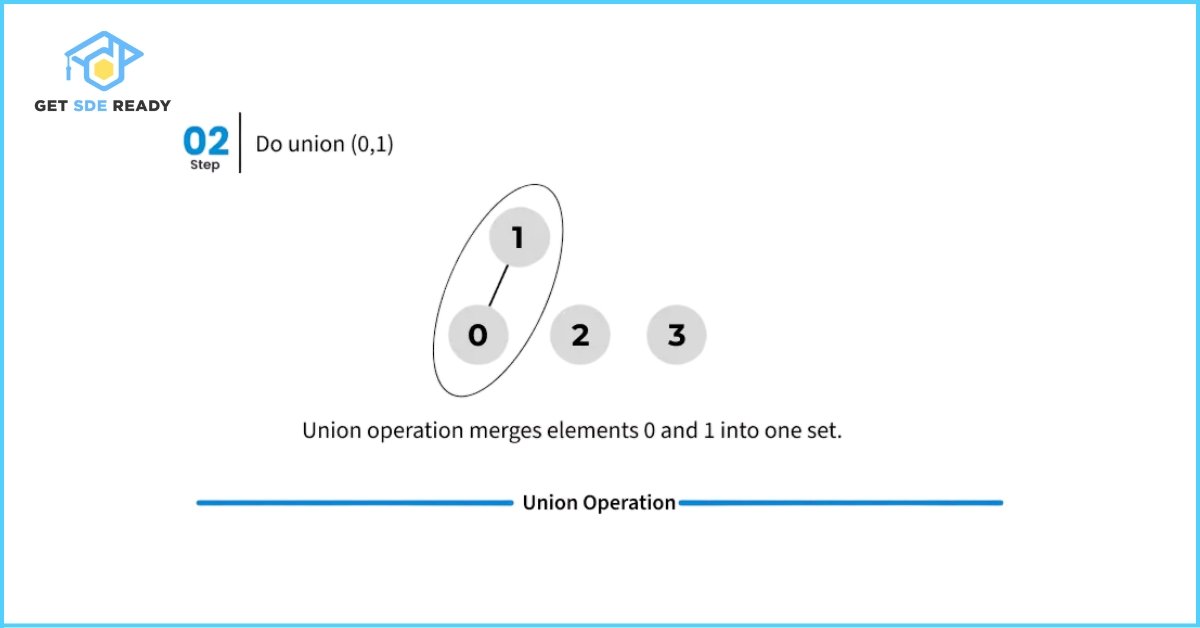
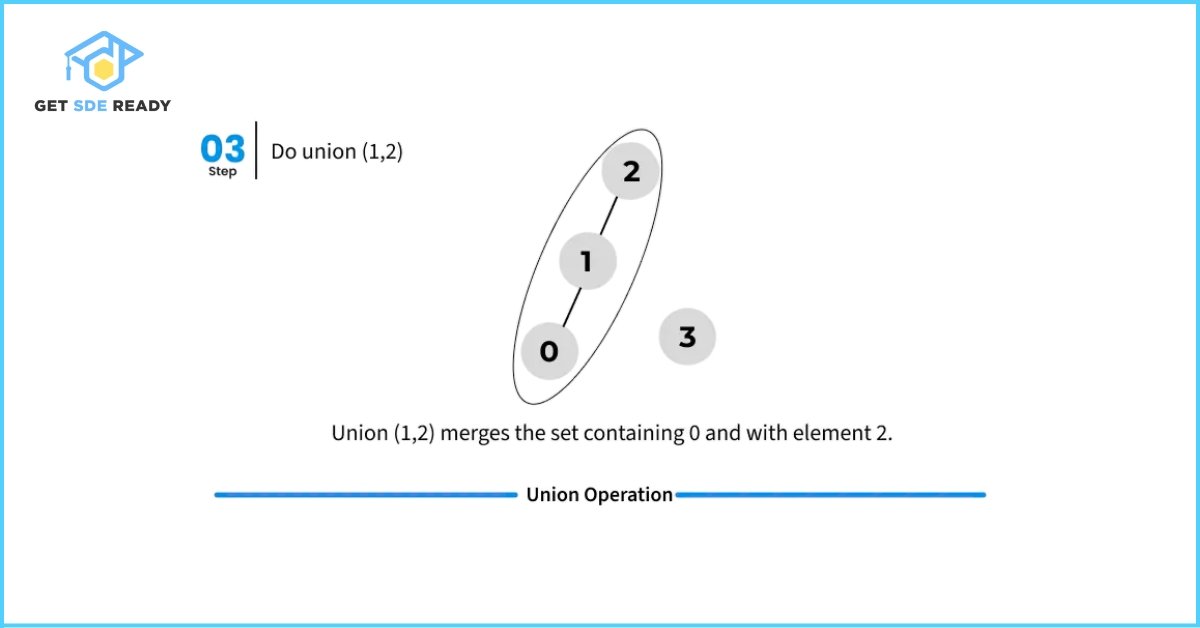
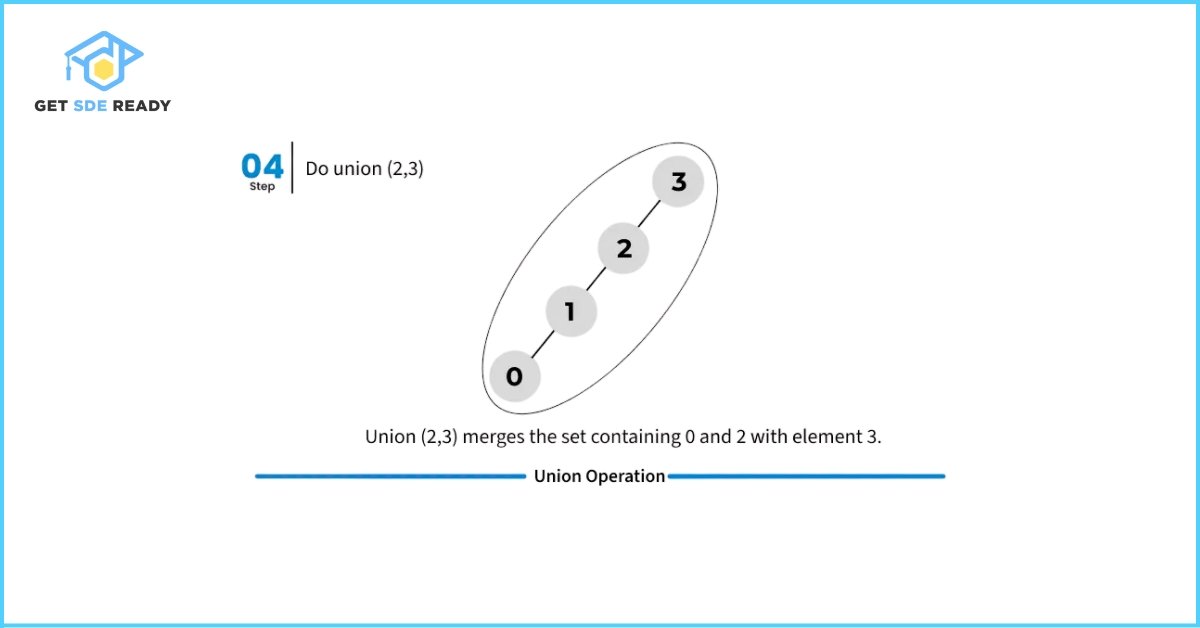
Optimization Techniques: Path Compression and Union by Rank/Size

To improve the efficiency of the Union-Find (Disjoint Set) algorithm, the key goal is to minimize the height of the trees representing individual sets. This is achieved through two widely used optimization techniques:

Path Compression
Union by Rank (or Size)

Path Compression

(Enhances the performance of the find() operation)
The core idea behind path compression is to flatten the structure of the tree during the find() process. When find(x) is executed, the algorithm traces up from element x to locate the root of the tree (the set’s representative). Once the root is identified, path compression directly connects x and all intermediate nodes to the root, making future find() operations significantly faster. After calling find(x), the path from x to its root is shortened by updating each node on the path to point directly to the root. This optimization leads to nearly constant time complexity for find operations in practice.

Union by Rank

(Optimizes the union() operation)
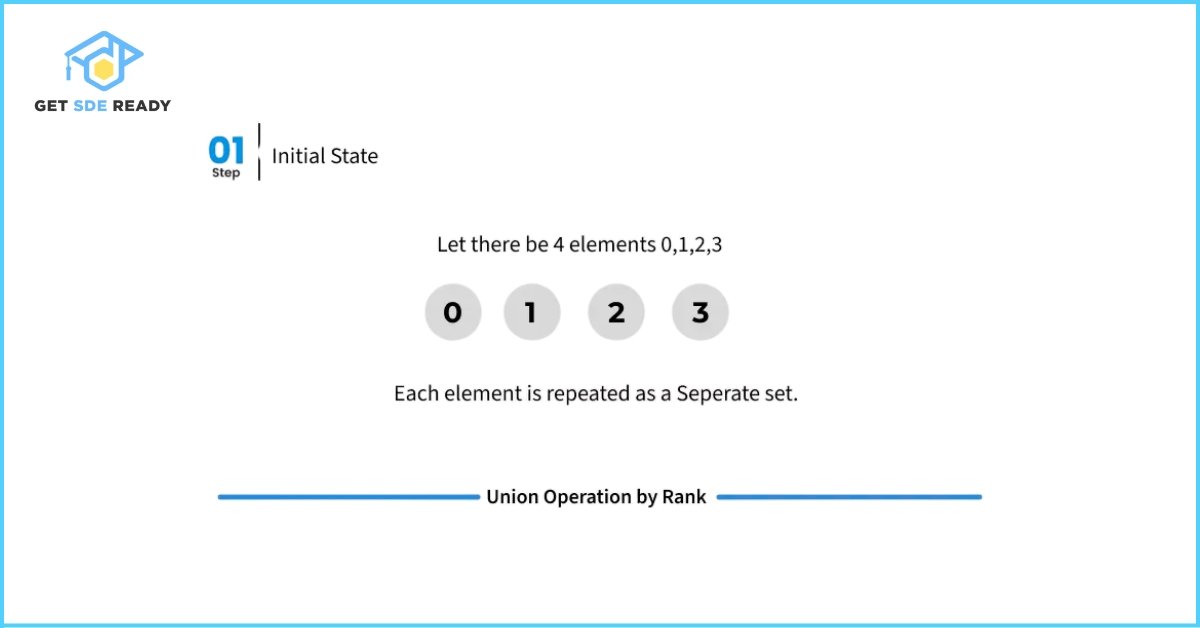
The concept of rank refers to the approximate height of the trees representing disjoint sets. To implement this optimization, we maintain an auxiliary array rank[], which has the same size as the parent[] array. If an element i is the representative (root) of a set, then rank[i] denotes the rank of that element.

Without path compression, the rank equals the height of the tree.
With path compression, the rank may exceed actual height but still manages balance effectively.

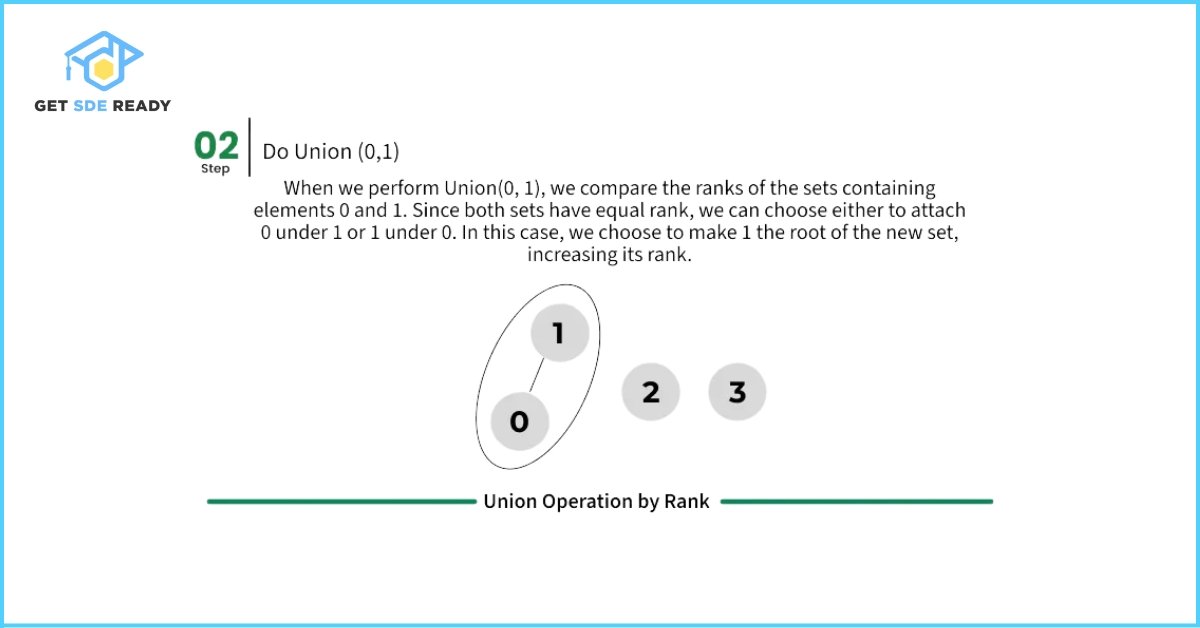
How It Works

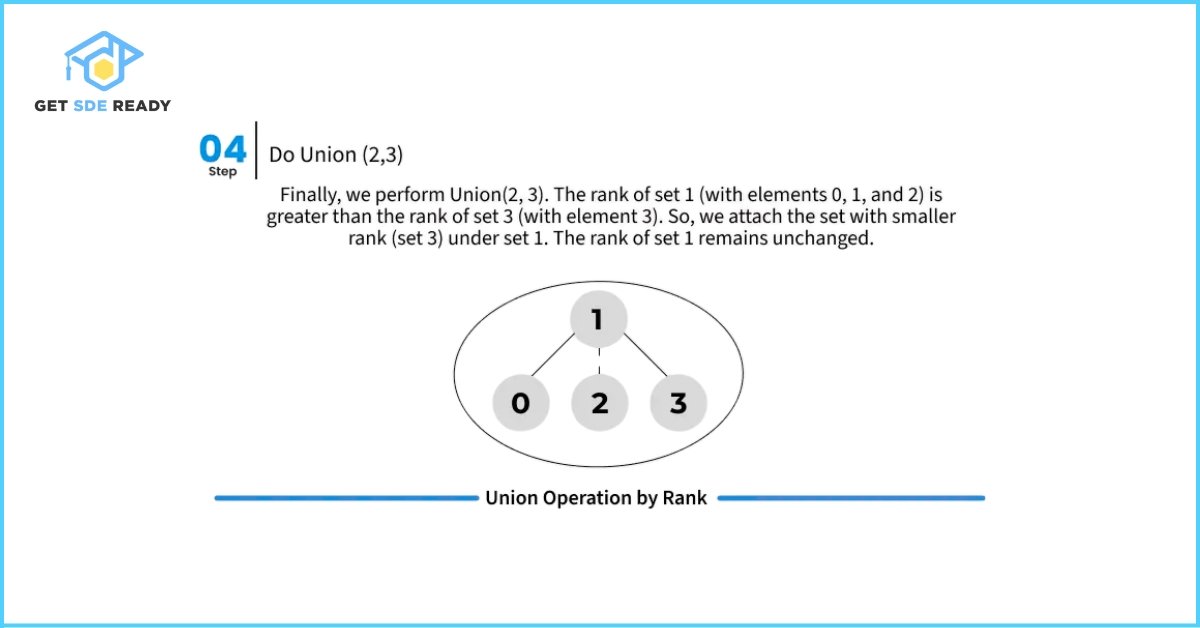
If rank[left] < rank[right]: attach the left tree under the right tree.
If rank[right] < rank[left]: attach the right tree under the left tree.
If equal: attach one under the other and increment the resulting root’s rank by one.

This keeps trees shallow and speeds up both union() and find() operations when combined with path compression.

Optimized Code Examples with Path Compression and Union by Rank.

				
					#include <iostream>
#include <vector>
using namespace std;

class DisjointUnionSets {
    vector<int> rank, parent;

public:
    DisjointUnionSets(int n) {
        rank.resize(n, 0);
        parent.resize(n);
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    int find(int i) {
        int root = parent[i];
        if (parent[root] != root) {
            return parent[i] = find(root);
        }
        return root;
    }

    void unionSets(int x, int y) {
        int xRoot = find(x);
        int yRoot = find(y);
        if (xRoot == yRoot) return;
        if (rank[xRoot] < rank[yRoot]) {
            parent[xRoot] = yRoot;
        } else if (rank[yRoot] < rank[xRoot]) {
            parent[yRoot] = xRoot;
        } else {
            parent[yRoot] = xRoot;
            rank[xRoot]++;
        }
    }
};

int main() {
    int n = 5;
    DisjointUnionSets dus(n);
    dus.unionSets(0, 2);
    dus.unionSets(4, 2);
    dus.unionSets(3, 1);
    if (dus.find(4) == dus.find(0))
        cout << "Yes\n";
    else
        cout << "No\n";
    if (dus.find(1) == dus.find(0))
        cout << "Yes\n";
    else
        cout << "No\n";
    return 0;
}

Output

0 1 2 3 4 5

Complexity Analysis of the Breadth-First Search (BFS) Algorithm

Time Complexity: O(V + E)

The BFS algorithm explores all vertices and edges in a graph. In the worst-case scenario, it visits every vertex and traverses every edge exactly once.

V = Number of vertices
E = Number of edges
Thus, the time complexity of BFS is O(V + E).

Auxiliary Space Complexity: O(V)

BFS uses a queue to manage the vertices to be explored. In the worst case, the queue can hold all vertices at once, especially in dense or fully connected graphs.
Hence, the auxiliary space required is O(V).

Applications of BFS in Graph Theory

Breadth-First Search is a foundational algorithm in computer science and graph theory, with several practical applications:

🔹 1. Shortest Path in Unweighted Graphs

BFS is commonly used to determine the shortest path between two nodes in an unweighted graph. By tracking each node’s parent during traversal, the path can be reconstructed efficiently.

🔹 2. Cycle Detection

BFS can detect cycles in both directed and undirected graphs. If a node is encountered more than once during traversal (excluding its immediate parent), a cycle exists.

🔹 3. Identifying Connected Components

In disconnected graphs, BFS can be used to identify connected components, where each component is a group of nodes that are mutually reachable.

🔹 4. Topological Sorting (for DAGs)

In a Directed Acyclic Graph (DAG), BFS helps in performing topological sorting by processing nodes in linear order such that each node appears before its dependents.

🔹 5. Level-Order Traversal of Binary Trees

BFS is ideal for level-order traversal in binary trees, where nodes are visited level by level from top to bottom.

🔹 6. Network Routing

BFS plays a key role in network routing algorithms, especially when finding the shortest path between two routers or devices in a network.

				
					import java.io.*;
import java.util.*;

class DisjointUnionSets {
    int[] rank, parent;
    public DisjointUnionSets(int n) {
        rank = new int[n];
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }
    public int find(int i) {
        int root = parent[i];
        if (parent[root] != root) {
            return parent[i] = find(root);
        }
        return root;
    }
    void union(int x, int y) {
        int xRoot = find(x), yRoot = find(y);
        if (xRoot == yRoot) return;
        if (rank[xRoot] < rank[yRoot]) {
            parent[xRoot] = yRoot;
        } else if (rank[yRoot] < rank[xRoot]) {
            parent[yRoot] = xRoot;
        } else {
            parent[yRoot] = xRoot;
            rank[xRoot]++;
        }
    }
}

public class Main {
    public static void main(String[] args) {
        int n = 5;
        DisjointUnionSets dus = new DisjointUnionSets(n);
        dus.union(0, 2);
        dus.union(4, 2);
        dus.union(3, 1);
        if (dus.find(4) == dus.find(0))
            System.out.println("Yes");
        else
            System.out.println("No");
        if (dus.find(1) == dus.find(0))
            System.out.println("Yes");
        else
            System.out.println("No");
    }
}

				
					class DisjointUnionSets {
    constructor(n) {
        this.rank = new Array(n).fill(0);
        this.parent = Array.from({ length: n }, (_, i) => i);
    }

    find(i) {
        let root = this.parent[i];
        if (this.parent[root] !== root) {
            return this.parent[i] = this.find(root);
        }
        return root;
    }

    unionSets(x, y) {
        const xRoot = this.find(x);
        const yRoot = this.find(y);
        if (xRoot === yRoot) return;
        if (this.rank[xRoot] < this.rank[yRoot]) {
            this.parent[xRoot] = yRoot;
        } else if (this.rank[yRoot] < this.rank[xRoot]) {
            this.parent[yRoot] = xRoot;
        } else {
            this.parent[yRoot] = xRoot;
            this.rank[xRoot]++;
        }
    }
}

const n = 5;
const dus = new DisjointUnionSets(n);
dus.unionSets(0, 2);
dus.unionSets(4, 2);
dus.unionSets(3, 1);
console.log(dus.find(4) === dus.find(0) ? 'Yes' : 'No');
console.log(dus.find(1) === dus.find(0) ? 'Yes' : 'No');

				
					class DisjointUnionSets:
    def __init__(self, n):
        self.rank = [0] * n
        self.parent = list(range(n))

    def find(self, i):
        root = self.parent[i]
        if self.parent[root] != root:
            self.parent[i] = self.find(root)
            return self.parent[i]
        return root

    def unionSets(self, x, y):
        xRoot = self.find(x)
        yRoot = self.find(y)
        if xRoot == yRoot:
            return
        if self.rank[xRoot] < self.rank[yRoot]:
            self.parent[xRoot] = yRoot
        elif self.rank[yRoot] < self.rank[xRoot]:
            self.parent[yRoot] = xRoot
        else:
            self.parent[yRoot] = xRoot
            self.rank[xRoot] += 1

if __name__ == '__main__':
    n = 5
    dus = DisjointUnionSets(n)
    dus.unionSets(0, 2)
    dus.unionSets(4, 2)
    dus.unionSets(3, 1)
    print('Yes' if dus.find(4) == dus.find(0) else 'No')
    print('Yes' if dus.find(1) == dus.find(0) else 'No')

Output After Optimized Operations

After performing the union operations and applying path compression or union by rank/size, the output for finding the representative (or parent) of each element is:

Element 0: Representative = 0

Element 1: Representative = 0

Element 2: Representative = 2

Element 3: Representative = 2

Element 4: Representative = 0

Elements 0, 1, and 4 are part of the same set with 0 as the representative.
Elements 2 and 3 belong to another set, with 2 as their representative.

These results confirm that the Union-Find operations have effectively grouped the elements into their correct disjoint sets, maintaining optimal structure due to the applied optimizations.

To practice with real problems and quizzes, explore our Essential DSA & Web Dev Courses that include Union-Find challenges.

Union by Size with Path Compression

Covers an alternative optimization, using size instead of rank.

				
					#include <iostream>
#include <vector>
using namespace std;

class UnionFind {
    vector<int> Parent;
    vector<int> Size;
public:
    UnionFind(int n) {      
        Parent.resize(n);
        for (int i = 0; i < n; i++) {
            Parent[i] = i;
        }
        Size.resize(n, 1);
    }

    int find(int i) {
        int root = Parent[i];
        if (Parent[root] != root) {
            return Parent[i] = find(root);
        }
        return root;
    }

    void unionBySize(int i, int j) {
        int irep = find(i);
        int jrep = find(j);
        if (irep == jrep) return;
        int isize = Size[irep];
        int jsize = Size[jrep];
        if (isize < jsize) {
            Parent[irep] = jrep;
            Size[jrep] += Size[irep];
        } else {
            Parent[jrep] = irep;
            Size[irep] += Size[jrep];
        }
    }
};

int main() {
    int n = 5;
    UnionFind unionFind(n);
    unionFind.unionBySize(0, 1);
    unionFind.unionBySize(2, 3);
    unionFind.unionBySize(0, 4);
    for (int i = 0; i < n; i++) {
        cout << "Element " << i << ": Representative = " 
             << unionFind.find(i) << endl;
    }
    return 0;
}

Output

0 1 2 3 4 5

Complexity Analysis of the Breadth-First Search (BFS) Algorithm

Time Complexity: O(V + E)

The BFS algorithm explores all vertices and edges in a graph. In the worst-case scenario, it visits every vertex and traverses every edge exactly once.

V = Number of vertices
E = Number of edges
Thus, the time complexity of BFS is O(V + E).

Auxiliary Space Complexity: O(V)

Applications of BFS in Graph Theory

Breadth-First Search is a foundational algorithm in computer science and graph theory, with several practical applications:

🔹 1. Shortest Path in Unweighted Graphs

BFS is commonly used to determine the shortest path between two nodes in an unweighted graph. By tracking each node’s parent during traversal, the path can be reconstructed efficiently.

🔹 2. Cycle Detection

BFS can detect cycles in both directed and undirected graphs. If a node is encountered more than once during traversal (excluding its immediate parent), a cycle exists.

🔹 3. Identifying Connected Components

In disconnected graphs, BFS can be used to identify connected components, where each component is a group of nodes that are mutually reachable.

🔹 4. Topological Sorting (for DAGs)

In a Directed Acyclic Graph (DAG), BFS helps in performing topological sorting by processing nodes in linear order such that each node appears before its dependents.

🔹 5. Level-Order Traversal of Binary Trees

BFS is ideal for level-order traversal in binary trees, where nodes are visited level by level from top to bottom.

🔹 6. Network Routing

BFS plays a key role in network routing algorithms, especially when finding the shortest path between two routers or devices in a network.

				
					import java.util.Arrays;

class UnionFind {
    private int[] Parent;
    private int[] Size;

    public UnionFind(int n) {
        Parent = new int[n];
        for (int i = 0; i < n; i++) {
            Parent[i] = i;
        }
        Size = new int[n];
        Arrays.fill(Size, 1);
    }

    public int find(int i) {
        int root = Parent[i];
        if (Parent[root] != root) {
            return Parent[i] = find(root);
        }
        return root;
    }

    public void unionBySize(int i, int j) {
        int irep = find(i);
        int jrep = find(j);
        if (irep == jrep) return;
        int isize = Size[irep];
        int jsize = Size[jrep];
        if (isize < jsize) {
            Parent[irep] = jrep;
            Size[jrep] += Size[irep];
        } else {
            Parent[jrep] = irep;
            Size[irep] += Size[jrep];
        }
    }
}

public class {
    public static void main(String[] args) {
        int n = 5;
        UnionFind unionFind = new UnionFind(n);
        unionFind.unionBySize(0, 1);
        unionFind.unionBySize(2, 3);
        unionFind.unionBySize(0, 4);
        for (int i = 0; i < n; i++) {
            System.out.println("Element " + i
                               + ": Representative = "
                               + unionFind.find(i));
        }
    }
}

				
					class UnionFind {
    constructor(n) {
        this.Parent = Array.from({ length: n }, (_, i) => i);
        this.Size = Array(n).fill(1);
    }

    find(i) {
        let root = this.Parent[i];
        if (this.Parent[root] !== root) {
            return this.Parent[i] = this.find(root);
        }
        return root;
    }

    unionBySize(i, j) {
        const irep = this.find(i);
        const jrep = this.find(j);
        if (irep === jrep) return;
        const isize = this.Size[irep];
        const jsize = this.Size[jrep];
        if (isize < jsize) {
            this.Parent[irep] = jrep;
            this.Size[jrep] += this.Size[irep];
        } else {
            this.Parent[jrep] = irep;
            this.Size[irep] += this.Size[jrep];
        }
    }
}

const n = 5;
const unionFind = new UnionFind(n);
unionFind.unionBySize(0, 1);
unionFind.unionBySize(2, 3);
unionFind.unionBySize(0, 4);
for (let i = 0; i < n; i++) {
    console.log(`Element ${i}: Representative = ${unionFind.find(i)}`);
}

				
					class UnionFind:
    def __init__(self, n):
        self.Parent = list(range(n))
        self.Size = [1] * n

    def find(self, i):
        root = self.Parent[i]
        if self.Parent[root] != root:
            self.Parent[i] = self.find(root)
            return self.Parent[i]
        return root

    def unionBySize(self, i, j):
        irep = self.find(i)
        jrep = self.find(j)
        if irep == jrep:
            return
        isize = self.Size[irep]
        jsize = self.Size[jrep]
        if isize < jsize:
            self.Parent[irep] = jrep
            self.Size[jrep] += self.Size[irep]
        else:
            self.Parent[jrep] = irep
            self.Size[irep] += self.Size[jrep]

n = 5
unionFind = UnionFind(n)
unionFind.unionBySize(0, 1)
unionFind.unionBySize(2, 3)
unionFind.unionBySize(0, 4)
for i in range(n):
    print(f'Element {i}: Representative = {unionFind.find(i)}')

.Output After Union by Size Operations

Element 0: Representative = 0

Element 1: Representative = 0

Element 2: Representative = 2

Element 3: Representative = 2

Element 4: Representative = 0

Elements 0, 1, and 4 are part of the same set with 0 as the representative.
Elements 2 and 3 belong to another set, with 2 as their representative.

These results confirm that the Union-Find operations, with size-based merging and path compression, have effectively grouped the elements into their correct disjoint sets while maintaining optimal structure.

Conclusion

Disjoint Set (Union-Find) is a cornerstone of efficient connectivity handling in algorithms. Mastering its naive implementation, recognizing its limitations, and applying optimizations like path compression and union by rank/size will equip you to solve a broad class of problems efficiently. Practice with real-world scenarios (friend groups, network connectivity, MSTs) and prepare with targeted interview materials to confidently tackle related challenges in coding rounds.

Ready to dive deeper? Join our community and access free updates and resources by signing up here. Continue leveling up your skills with our comprehensive courses in DSA, Web Development, System Design, and more.

What is the time complexity of Union-Find with path compression and union by rank?

With both optimizations, each find or union operation runs in nearly constant amortized time (O(α(N)), where α is the inverse Ackermann function). You can study this concept in depth in a dedicated Disjoint Set module within a comprehensive DSA course.

How do I apply Disjoint Set to detect cycles in a graph?

To detect a cycle in an undirected graph, iterate through edges; for each edge (u, v), if find(u) equals find(v), a cycle exists; otherwise, perform union(u, v). Many algorithm courses and problem sets include cycle detection examples using Union-Find.

Can Disjoint Set be used in dynamic connectivity problems?

Yes. DSU efficiently handles merging of components and connectivity queries in dynamic settings. Look for modules on dynamic connectivity or advanced DSU variants in a full DSA curriculum.

What’s the difference between union by rank and union by size?

Both aim to keep trees shallow. Union by rank uses an estimate of tree height, while union by size attaches the smaller tree under the larger based on node count. Many tutorials compare these approaches side by side in their Union-Find sections.

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Introduction to Disjoint Set (Union-Find Algorithm)

Scenario: Friendship Connections

Establish a New Friendship

Verify a Friendship Link

Examples

Determining If Two Individuals Belong to the Same Group

Key Concepts to Understand

Set Initialization and Resolution

Group Membership Check

Data Structures Used

Array (Parent[])

Tree Structure

Core Operations in Disjoint Set

Find Operation

Union Operation

Code Examples

BFS Traversal Output:

Output

BFS in a Disconnected Graph

Output

BFS in a Disconnected Graph

Network Routing in Computer Networking

Flight Connectivity in Aviation

Geographic Information Systems (GIS)

Kleene’s Algorithm and Formal Language Theory

Output Example

Optimization Techniques: Path Compression and Union by Rank/Size

Path Compression

Union by Rank

How It Works

Optimized Code Examples with Path Compression and Union by Rank.

Output

Complexity Analysis of the Breadth-First Search (BFS) Algorithm

Time Complexity: O(V + E)

Auxiliary Space Complexity: O(V)

Applications of BFS in Graph Theory

🔹 1. Shortest Path in Unweighted Graphs

🔹 2. Cycle Detection

🔹 3. Identifying Connected Components

🔹 4. Topological Sorting (for DAGs)

🔹 5. Level-Order Traversal of Binary Trees

🔹 6. Network Routing

Output After Optimized Operations

Union by Size with Path Compression

Output

Complexity Analysis of the Breadth-First Search (BFS) Algorithm

Time Complexity: O(V + E)

Auxiliary Space Complexity: O(V)

Applications of BFS in Graph Theory

🔹 1. Shortest Path in Unweighted Graphs

🔹 2. Cycle Detection

🔹 3. Identifying Connected Components

🔹 4. Topological Sorting (for DAGs)

🔹 5. Level-Order Traversal of Binary Trees

🔹 6. Network Routing

.Output After Union by Size Operations

Conclusion

What is the time complexity of Union-Find with path compression and union by rank?

How do I apply Disjoint Set to detect cycles in a graph?

Can Disjoint Set be used in dynamic connectivity problems?

What’s the difference between union by rank and union by size?

Accelerate your Path to a Product based Career

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design