Data Structures and Algorithms

DSA Interview Questions

Step-by-Step Guide to Master Recursion in DSA

Have you ever felt stuck trying to wrap your head around recursion in data structures and algorithms? You’re not alone—it’s a concept that trips up many aspiring developers at first, but once you get it, it opens up a world of elegant problem-solving. If you’re eager to accelerate your learning with free resources and stay updated on the latest DSA tips, sign up here for exclusive access to our beginner-friendly guides and course previews. In this comprehensive guide, we’ll break down recursion step by step, from the fundamentals to advanced techniques, helping you build the confidence to tackle recursive problems like a pro.

What is Recursion and Why Does It Matter in DSA?

Recursion is a powerful programming technique where a function calls itself to solve a problem by breaking it down into smaller, more manageable subproblems. At its core, it’s about defining a problem in terms of itself, which might sound circular, but it’s incredibly useful for tasks like tree traversals or sorting algorithms. Think of it as a Russian doll: each layer reveals a smaller version until you reach the tiniest one.

In data structures and algorithms (DSA), recursion shines in scenarios where problems have a natural hierarchical structure. For instance, calculating the Fibonacci sequence or traversing a binary tree becomes intuitive with recursion. According to experts like Donald Knuth in “The Art of Computer Programming,” recursion simplifies complex algorithms by mirroring mathematical induction. Statistically, recursion appears in about 20-30% of coding interview questions at top tech companies, making it essential for career growth.

Why master it? Beyond interviews, recursion builds logical thinking. It underpins divide-and-conquer strategies in algorithms like merge sort, which can reduce time complexity from O(n²) to O(n log n). If you’re diving into DSA, consider exploring structured courses to solidify these concepts—our DSA course offers hands-on modules to get you started.

The Building Blocks of Recursion

Every recursive function has two key parts: the base case and the recursive case.

Base Case: This is the stopping point. Without it, you’d end up with infinite recursion and a stack overflow error. For example, in factorial, the base case is when n=0 or n=1, returning 1.

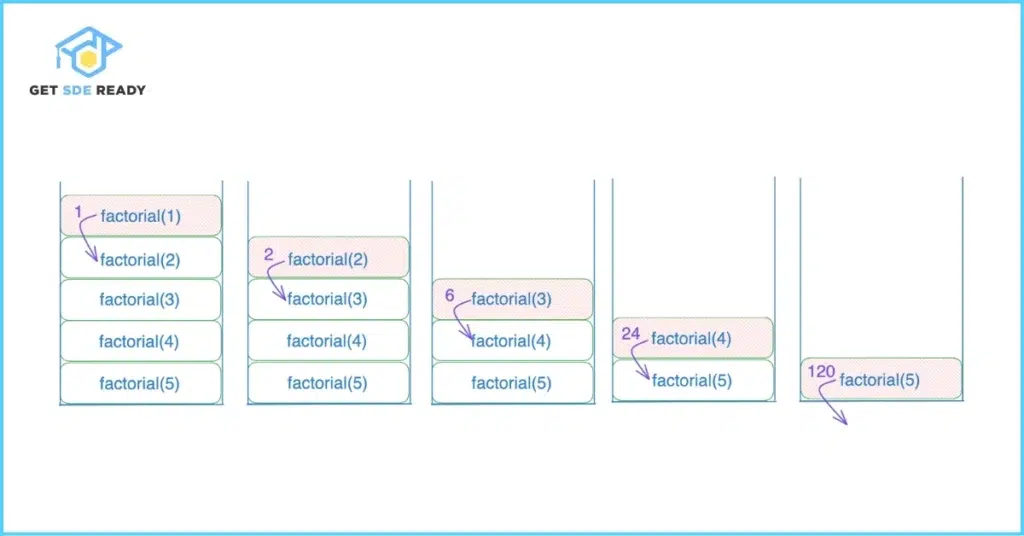
Recursive Case: Here, the function calls itself with a modified input that moves closer to the base case. Like in factorial(n) = n * factorial(n-1).

Visualize this with the call stack: each recursive call pushes a new frame onto the stack, holding local variables until the base case is hit, then it unwinds, combining results.

Recursion vs. Iteration: When to Choose What

Recursion isn’t always the go-to; sometimes iteration is more efficient. Iteration uses loops and constant space (O(1)), while recursion can consume O(n) space due to the call stack. But recursion often leads to cleaner, more readable code for problems like graph traversals.

Here’s a quick comparison:

Aspect	Recursion	Iteration
Space Complexity	O(n) (call stack)	O(1)
Time Complexity	Often similar, but can be worse with overlaps	Typically efficient
Code Readability	High for hierarchical problems	High for linear processes
Risk	Stack overflow	Infinite loops afteracademy.com Comparison table of iterative vs. recursive approaches in DSA.

Step 1: Grasping the Fundamentals with Simple Examples

Let’s start small. We’ll use Python for examples, but the principles apply across languages.

Factorial: Your First Recursive Function

The factorial of a number n is n! = n × (n-1) × … × 1. Here’s the recursive version:

				
					def factorial(n):
    if n == 0 or n == 1:  # Base case
        return 1
    else:  # Recursive case
        return n * factorial(n - 1)

Calling factorial(5) unfolds like this: 5 * 4 * 3 * 2 * 1 = 120. Trace it mentally: the function calls itself until n=1, then multiplies back up.
Actionable tip: Write this out on paper, drawing the call tree to visualize the process. If you’re new to coding, our crash course can help build these basics quickly.
Fibonacci Sequence: Spotting Inefficiencies

The Fibonacci sequence is another classic: fib(n) = fib(n-1) + fib(n-2), with fib(0)=0, fib(1)=1.

				
					def fibonacci(n):
    if n <= 1:
        return n
    return fibonacci(n-1) + fibonacci(n-2)

This naive approach has exponential time complexity (O(2^n)) due to overlapping subproblems—fib(3) is calculated multiple times.

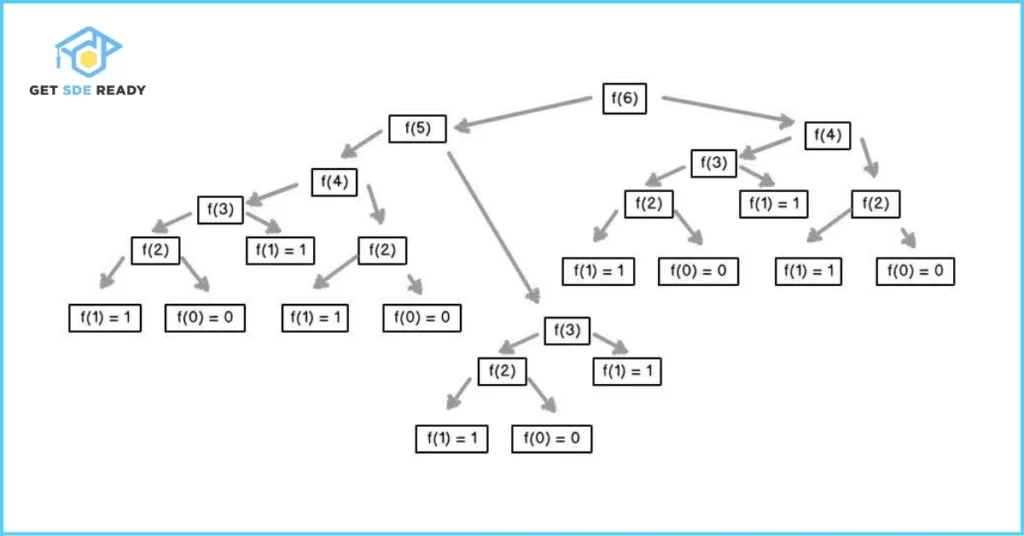
Recursion tree diagram for Fibonacci sequence, highlighting overlapping subproblems.

To master this, practice rewriting it iteratively for comparison.

Step 2: Identifying Common Recursion Patterns

As you progress, you’ll notice patterns in recursive problems.

Divide and Conquer

Break the problem into non-overlapping subproblems, solve them recursively, and combine results. Examples: Merge sort, quicksort.

Backtracking

Explore all possible solutions by building candidates incrementally and abandoning (“backtracking”) when invalid. Useful for puzzles like N-Queens or Sudoku.

Tree and Graph Traversals

Recursion naturally fits trees: inorder, preorder, postorder traversals.

For graphs, depth-first search (DFS) uses recursion to explore as far as possible along each branch.

Tip: Always check for cycles in graphs to avoid infinite recursion.

If data science intrigues you, recursion also appears in decision trees—explore our data science course for applications.

Step 3: Practice with Real-World Problems

Theory is great, but practice cements mastery. Here are 15 common recursion problems, drawn from platforms like LeetCode and GeeksforGeeks. We’ll explain a few in depth, with code.

Easy Problems

Print Numbers from 1 to N: Recursively print without loops.

				
					def print_numbers(n):
    if n == 0:
        return
    print_numbers(n-1)

    print(n)

Sum of Array Elements: Recurse to add elements.
Reverse a String: Swap characters recursively.

Medium Problems

Generate Parentheses (LeetCode #22): Generate all valid combinations.

Approach: Use backtracking to add open/close parentheses, ensuring balance.

				
					
def generate_parenthesis(n):
    def backtrack(s, open_count, close_count):
        if len(s) == 2 * n:
            result.append(s)
            return
        if open_count < n:
            backtrack(s + '(', open_count + 1, close_count)
        if close_count < open_count:
            backtrack(s + ')', open_count, close_count + 1)
    
    result = []
    backtrack('', 0, 0)
    return result

1. Subsets (LeetCode #78): Find all subsets of a set.
  Use recursion to include/exclude each element.
2. Permutations of a String: Generate all arrangements.
3. Merge Two Sorted Lists (LeetCode #21): Recursively merge.
4. Binary Tree Inorder Traversal (LeetCode #94).
Hard Problems
1. Word Search II (LeetCode #212): Backtrack on a grid.
2. Sudoku Solver (LeetCode #37): Try numbers 1-9, backtrack on failure.
3. N-Queens (LeetCode #51).
4. Longest Increasing Path in a Matrix (LeetCode #329).
5. Burst Balloons (LeetCode #312): Dynamic programming with recursion.
6. Regular Expression Matching (LeetCode #10).
7. Edit Distance (LeetCode #72).
For each, start by drawing the recursion tree. Practice on LeetCode—aim for 50 problems to build intuition.
Step 4: Debugging and Common Pitfalls
Recursion can be tricky to debug. Common issues:
- Missing Base Case: Leads to stack overflow.
- Off-by-One Errors: Wrong bounds in arrays/trees.
- Overlapping Subproblems: Use memoization (caching results) to optimize.
Tools like Python’s debugger (pdb) or visualizing the stack help. Always test with small inputs first.
Step 5: Optimization Techniques
Memoization
Store computed results to avoid redundant calculations. For Fibonacci:

				
					
def fibonacci_memo(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)
    return memo[n]

This drops time from O(2^n) to O(n).

Tail Recursion

When the recursive call is the last operation, compilers can optimize to use constant space. Not all languages support it fully, but it’s worth knowing.

Advanced Topics: Beyond Basics

Once comfortable, explore:

Mutual Recursion: Functions calling each other.
Recursion in Functional Programming: Pure functions enhance clarity.
Recursion in Web Development: Used in parsing JSON or DOM trees. If interested, our web development course covers this.

Recursion also ties into fractals and AI search algorithms.

Conclusion: Your Path to Mastery

Mastering recursion in DSA is about practice and patience. Start with basics, build patterns, optimize, and apply to real problems. You’ve got this—keep coding! For more structured learning, dive into our DSA course. What’s your next recursive challenge? Share in the comments and let’s discuss.

FAQs

What is recursion in DSA?

Recursion in data structures and algorithms is a method where a function solves problems by calling itself with smaller inputs until reaching a base case.

How does recursion differ from iteration?

Recursion uses function calls and stack memory for hierarchical problems, while iteration employs loops for efficient, linear processing without extra space.

Why is a base case important in recursion?

A base case prevents infinite recursion and stack overflow by providing a termination condition for the recursive calls.

What are common recursion examples in algorithms?

Common examples include factorial calculation, Fibonacci sequence, tree traversals like inorder, and backtracking problems such as generating permutations.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 52% OFF
₹25,000.00 ₹11,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

arun@getsdeready.com

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Step-by-Step Guide to Master Recursion in DSA

What is Recursion and Why Does It Matter in DSA?

The Building Blocks of Recursion

Recursion vs. Iteration: When to Choose What

Step 1: Grasping the Fundamentals with Simple Examples

Factorial: Your First Recursive Function

Fibonacci Sequence: Spotting Inefficiencies

Step 2: Identifying Common Recursion Patterns

Divide and Conquer

Backtracking

Tree and Graph Traversals

Step 3: Practice with Real-World Problems

Easy Problems

Medium Problems

Hard Problems

Step 4: Debugging and Common Pitfalls

Step 5: Optimization Techniques

Memoization

Tail Recursion

Advanced Topics: Beyond Basics

Conclusion: Your Path to Mastery

FAQs

What is recursion in DSA?

How does recursion differ from iteration?

Why is a base case important in recursion?

What are common recursion examples in algorithms?

DSA, High & Low Level System Designs

Buy for 52% OFF ₹25,000.00 ₹11,999.00

Accelerate your Path to a Product based Career

Mental Ability

DSA, High & Low Level System Designs

Buy for 52% OFF ₹25,000.00 ₹11,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 51% OFF ₹35,000.00 ₹16,999.00

Low & High Level System Design

Buy for 60% OFF ₹20,000.00 ₹7,999.00

Mastering Mern Stack (WEB DEVELOPMENT)

Buy for 53% OFF ₹15,000.00 ₹6,999.00

Mastering Data Structures & Algorithms

Buy for 40% OFF ₹9,999.00 ₹5,999.00

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Buy for 52% OFF
₹25,000.00 ₹11,999.00

Buy for 52% OFF
₹25,000.00 ₹11,999.00

Buy for 51% OFF
₹35,000.00 ₹16,999.00

Buy for 60% OFF
₹20,000.00 ₹7,999.00

Buy for 53% OFF
₹15,000.00 ₹6,999.00

Buy for 40% OFF
₹9,999.00 ₹5,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design