Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Introduction to High-Level System Design
System Design Fundamentals
- Functional vs. Non-Functional Requirements
- Scalability, Availability, and Reliability
- Latency and Throughput Considerations
- Load Balancing Strategies
Architectural Patterns
- Monolithic vs. Microservices Architecture
- Layered Architecture
- Event-Driven Architecture
- Serverless Architecture
- Model-View-Controller (MVC) Pattern
- CQRS (Command Query Responsibility Segregation)
Scaling Strategies
- Vertical Scaling vs. Horizontal Scaling
- Sharding and Partitioning
- Data Replication and Consistency Models
- Load Balancing Strategies
- CDN and Edge Computing
Database Design in HLD
- SQL vs. NoSQL Databases
- CAP Theorem and its Impact on System Design
- Database Indexing and Query Optimization
- Database Sharding and Partitioning
- Replication Strategies
API Design and Communication
Caching Strategies
- Types of Caching
- Cache Invalidation Strategies
- Redis vs. Memcached
- Cache-Aside, Write-Through, and Write-Behind Strategies
Message Queues and Event-Driven Systems
- Kafka vs. RabbitMQ vs. SQS
- Pub-Sub vs. Point-to-Point Messaging
- Handling Asynchronous Workloads
- Eventual Consistency in Distributed Systems
Security in System Design
Observability and Monitoring
- Logging Strategies (ELK Stack, Prometheus, Grafana)
- API Security Best Practices
- Secure Data Storage and Access Control
- DDoS Protection and Rate Limiting
Real-World System Design Case Studies
- Distributed locking (Locking and its Types)
- Memory leaks and Out of memory issues
- HLD of YouTube
- HLD of WhatsApp
System Design Interview Questions
- Adobe System Design Interview Questions
- Top Atlassian System Design Interview Questions
- Top Amazon System Design Interview Questions
- Top Microsoft System Design Interview Questions
- Top Meta (Facebook) System Design Interview Questions
- Top Netflix System Design Interview Questions
- Top Uber System Design Interview Questions
- Top Google System Design Interview Questions
- Top Apple System Design Interview Questions
- Top Airbnb System Design Interview Questions
- Top 10 System Design Interview Questions
- Mobile App System Design Interview Questions
- Top 20 Stripe System Design Interview Questions
- Top Shopify System Design Interview Questions
- Top 20 System Design Interview Questions
- Top Advanced System Design Questions
- Most-Frequented System Design Questions in Big Tech Interviews
- What Interviewers Look for in System Design Questions
- Critical System Design Questions to Crack Any Tech Interview
- Top 20 API Design Questions for System Design Interviews
- Top 10 Steps to Create a System Design Portfolio for Developers
Prim’s Algorithm for Minimum Spanning Tree (MST)
Prim’s Algorithm is a classic Greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, undirected graph. Similar to Kruskal’s algorithm, Prim’s algorithm works by incrementally building the MST. However, instead of sorting all edges upfront, it grows the MST one edge at a time from a selected starting node.
- This approach begins with an empty MST and uses two distinct sets of vertices:
- One set contains the vertices already included in the MST.
- The other set includes vertices not yet part of the MST.
At each iteration, the algorithm examines all edges connecting the two sets and selects the edge with the minimum weight. Once chosen, the algorithm adds the corresponding vertex to the MST set.
In graph theory, edges that connect two disjoint sets of vertices are referred to as Cut Edges, and their connecting vertices are known as Articulation Points (or Cut Vertices). Prim’s Algorithm, at every step, identifies such a cut and adds the minimum weight edge to the growing MST.
How Prim’s Algorithm Works
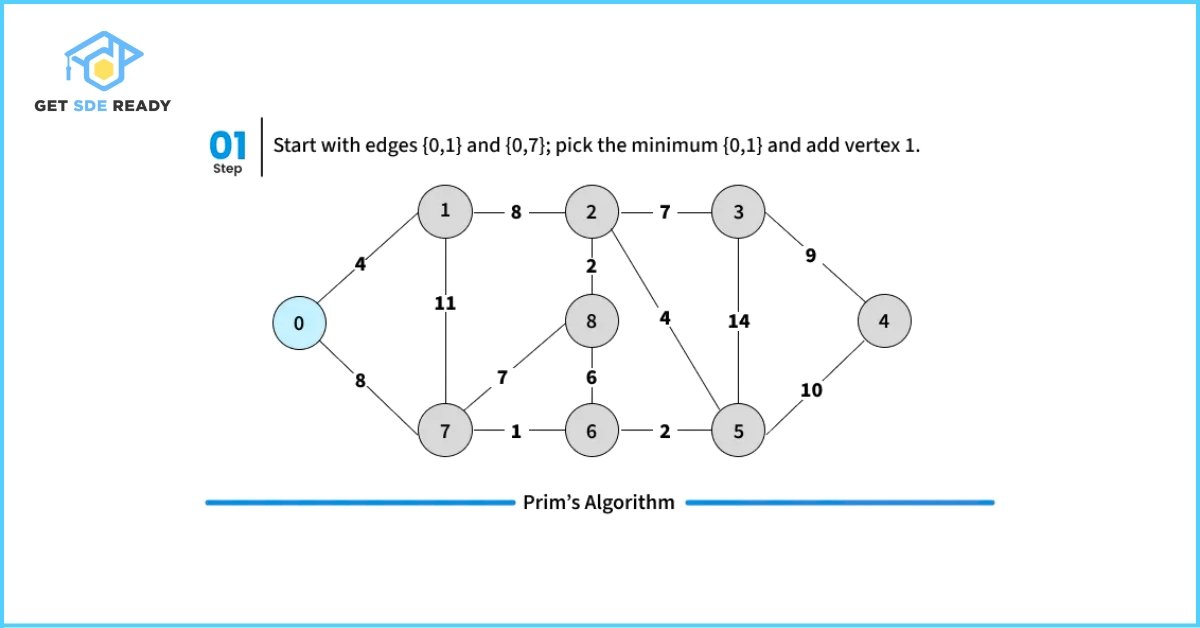
- Step 1: Choose any arbitrary vertex as the starting point for the MST.
- In the diagram example below, vertex 0 is selected.
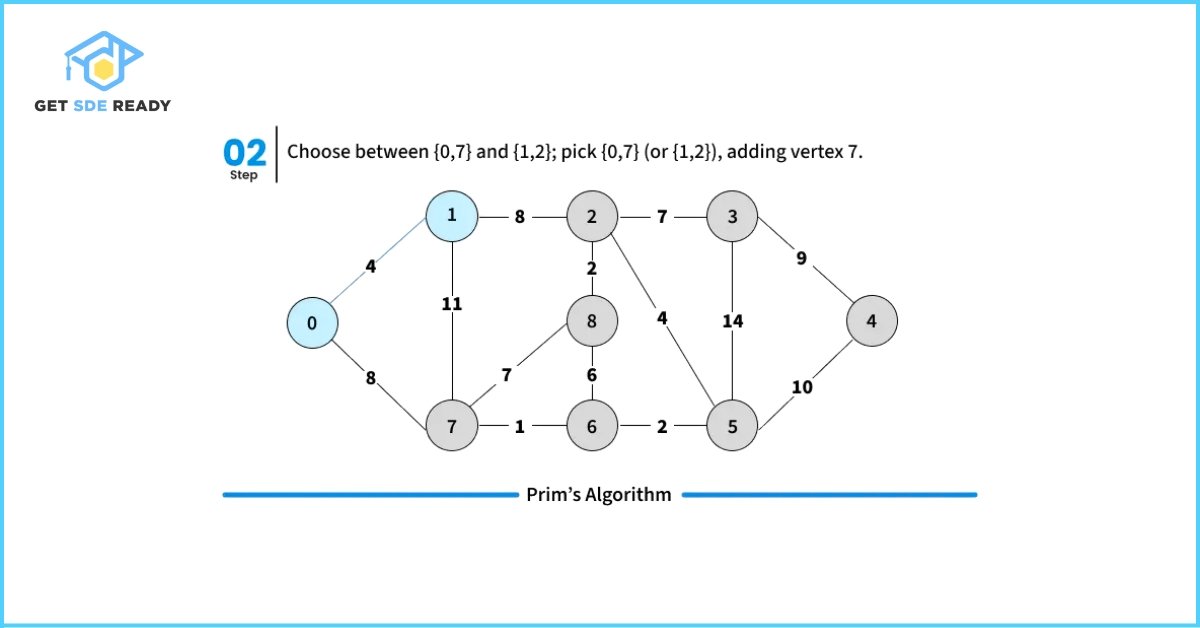
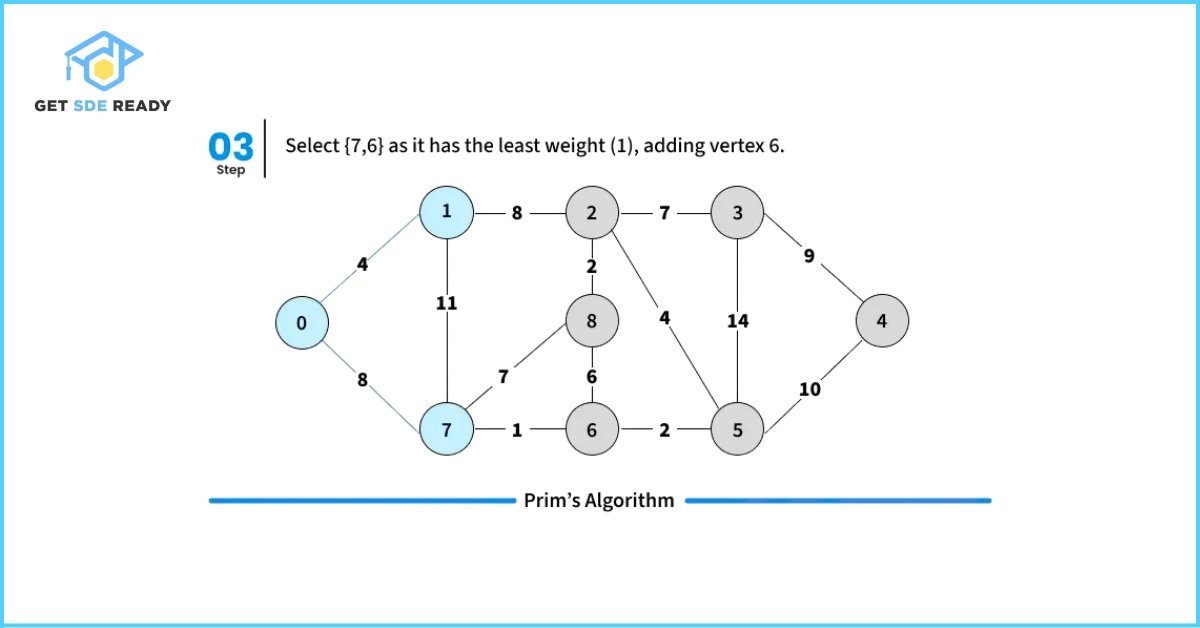
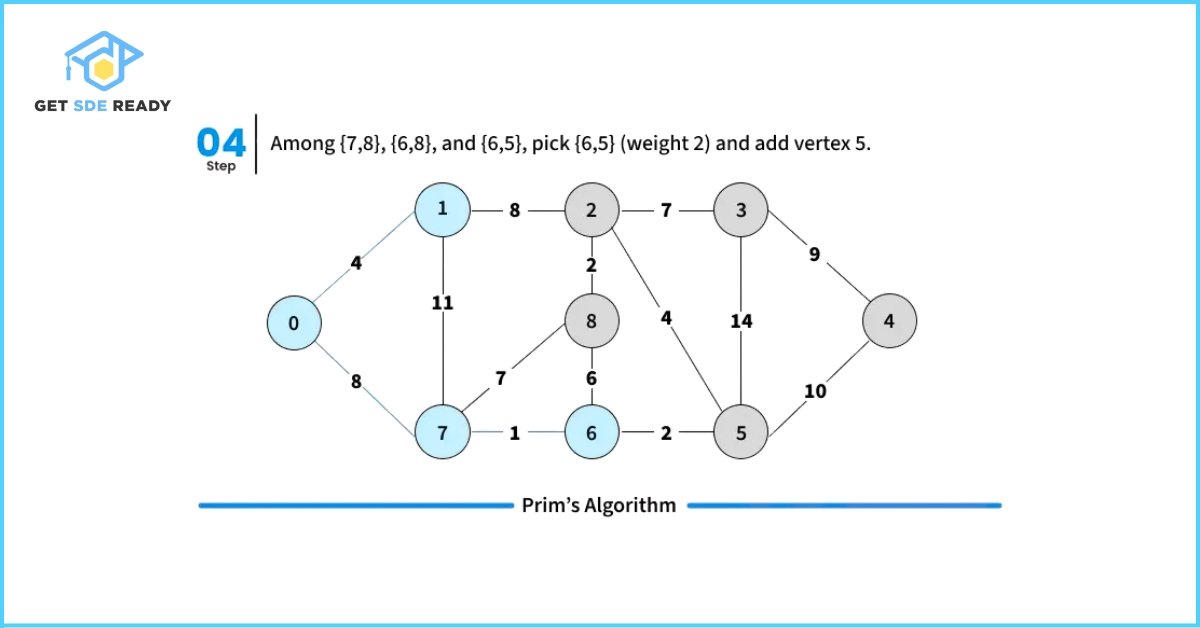
- Step 2: Repeat steps 3 to 5 while there are still fringe vertices (vertices not yet included in the MST).
- Step 3: Identify all the edges connecting vertices in the MST with the fringe vertices.
- Step 4: From these connecting edges, find the edge with the smallest weight.
- Step 5: Add the selected minimum edge to the MST.
- Since the algorithm only considers edges between the MST and fringe vertices, cycles are never formed.
- Step 6: Once all vertices are included in the MST, return the final tree and terminate the algorithm.


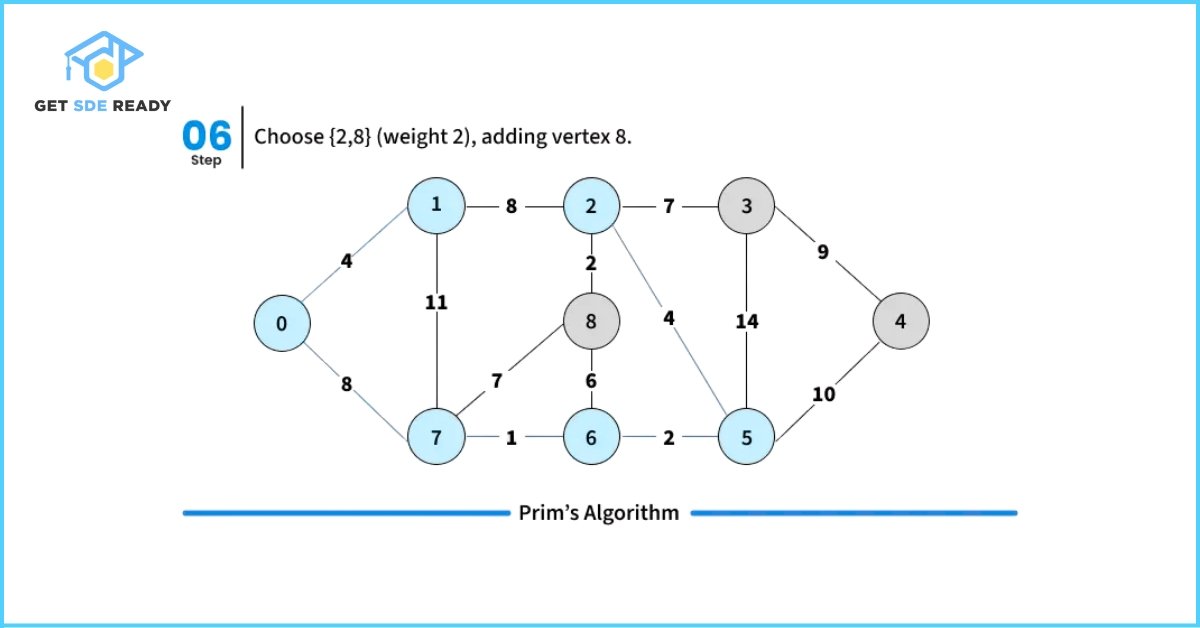
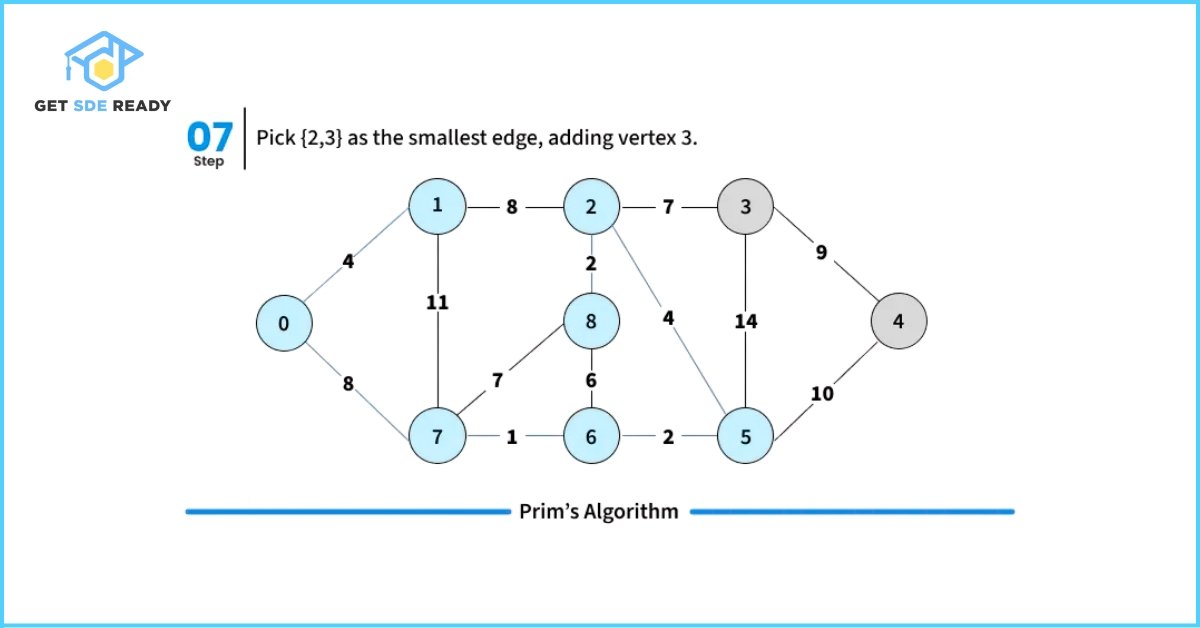
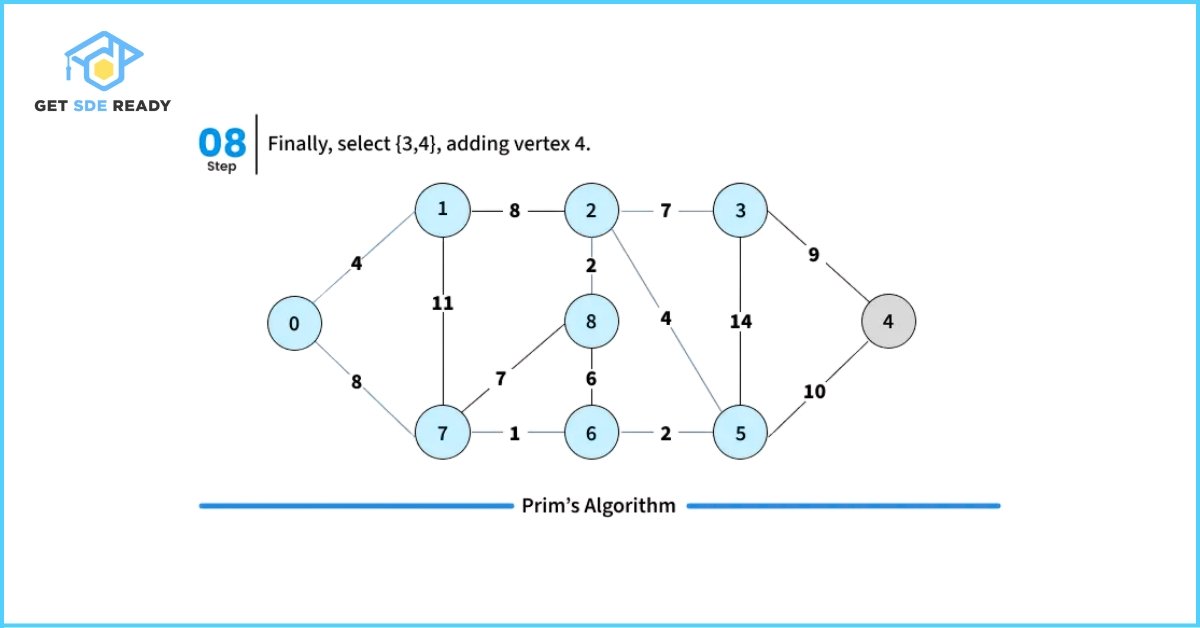

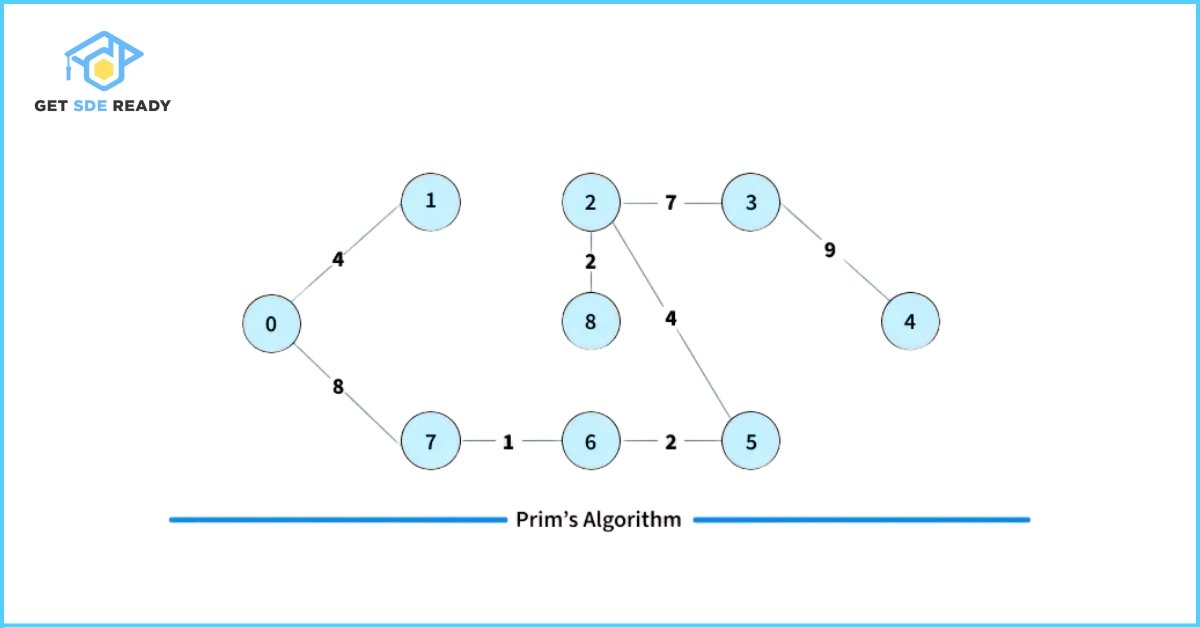

How to Implement Prim’s Algorithm?
To implement Prim’s Algorithm for finding the Minimum Spanning Tree (MST) of a graph, follow the steps outlined below:
- Initialize a set mstSet to keep track of the vertices that have already been included in the MST.
- Assign a key value to each vertex in the graph. Initially, set all key values to INFINITY. For the starting vertex, assign the key value 0 so that it is selected first.
- Repeat the following steps until mstSet includes all vertices:
- Select a vertex u that is not yet in mstSet and has the minimum key value.
- Add vertex u to mstSet, marking it as included in the MST.
- Update the key values of all adjacent vertices of u. For each adjacent vertex v, if the edge weight between u and v is less than the current key value of v, update the key value of v to the weight of edge u-v.
- Select a vertex u that is not yet in mstSet and has the minimum key value.
The core idea behind using key values is to ensure that at each step, the algorithm selects the lightest possible edge connecting the current MST to a new vertex. These key values are maintained only for vertices not yet included in the MST, representing the minimum edge weight connecting them to the already included set.
Below is the implementation of this approach:
// A C++ program for Prim's Minimum
// Spanning Tree (MST) algorithm. The program is
// for adjacency matrix representation of the graph
#include <bits/stdc++.h>
using namespace std;
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
int minKey(vector<int> &key, vector<bool> &mstSet) {
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < mstSet.size(); v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
void printMST(vector<int> &parent, vector<vector<int>> &graph) {
cout << "Edge \tWeight\n";
for (int i = 1; i < graph.size(); i++)
cout << parent[i] << " - " << i << " \t"
<< graph[parent[i]][i] << " \n";
}
// Function to construct and print MST for
// a graph represented using adjacency
// matrix representation
void primMST(vector<vector<int>> &graph) {
int V = graph.size();
// Array to store constructed MST
vector<int> parent(V);
// Key values used to pick minimum weight edge in cut
vector<int> key(V);
// To represent set of vertices included in MST
vector<bool> mstSet(V);
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is picked as first
// vertex.
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the
// set of vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of
// the adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for vertices
// not yet included in MST Update the key only
// if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false
&& graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// Print the constructed MST
printMST(parent, graph);
}
// Driver's code
int main() {
vector<vector<int>> graph = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
primMST(graph);
return 0;
}
// A Java program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency matrix
// representation of the graph
import java.io.*;
import java.lang.*;
import java.util.*;
class MST {
// A utility function to find the vertex with minimum
// key value, from the set of vertices not yet included
// in MST
int minKey(int key[], Boolean mstSet[])
{
// Initialize min value
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < mstSet.length; v++)
if (mstSet[v] == false && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
// A utility function to print the constructed MST
// stored in parent[]
void printMST(int parent[], int graph[][])
{
System.out.println("Edge \tWeight");
for (int i = 1; i < graph.length; i++)
System.out.println(parent[i] + " - " + i + "\t"
+ graph[parent[i]][i]);
}
// Function to construct and print MST for a graph
// represented using adjacency matrix representation
void primMST(int graph[][])
{
int V = graph.length;
// Array to store constructed MST
int parent[] = new int[V];
// Key values used to pick minimum weight edge in
// cut
int key[] = new int[V];
// To represent set of vertices included in MST
Boolean mstSet[] = new Boolean[V];
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++) {
key[i] = Integer.MAX_VALUE;
mstSet[i] = false;
}
// Always include first 1st vertex in MST.
// Make key 0 so that this vertex is
// picked as first vertex
key[0] = 0;
// First node is always root of MST
parent[0] = -1;
// The MST will have V vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of
// vertices not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the
// adjacent vertices of the picked vertex.
// Consider only those vertices which are not
// yet included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent
// vertices of m mstSet[v] is false for
// vertices not yet included in MST Update
// the key only if graph[u][v] is smaller
// than key[v]
if (graph[u][v] != 0 && mstSet[v] == false
&& graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
// Print the constructed MST
printMST(parent, graph);
}
public static void main(String[] args)
{
MST t = new MST();
int graph[][] = new int[][] { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
// Print the solution
t.primMST(graph);
}
}
// Number of vertices in the graph
let V = 5;
// A utility function to find the vertex with
// minimum key value, from the set of vertices
// not yet included in MST
function minKey(key, mstSet) {
// Initialize min value
let min = Number.MAX_VALUE, min_index = -1;
for (let v = 0; v < V; v++)
if (!mstSet[v] && key[v] < min) {
min = key[v];
min_index = v;
}
return min_index;
}
// A utility function to print the
// constructed MST stored in parent[]
function printMST(parent, graph) {
console.log("Edge Weight");
for (let i = 1; i < V; i++)
console.log(parent[i] + " - " + i + " " + graph[parent[i]][i]);
}
// Function to construct and print MST for
// a graph represented using adjacency matrix
function primMST(graph) {
// Array to store constructed MST
let parent = new Array(V);
// Key values used to pick minimum weight edge in cut
let key = new Array(V);
// To represent set of vertices included in MST
let mstSet = new Array(V);
// Initialize all keys as INFINITE
for (let i = 0; i < V; i++) {
key[i] = Number.MAX_VALUE;
mstSet[i] = false;
}
// Always include first vertex in MST.
key[0] = 0;
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (let count = 0; count < V - 1; count++) {
// Pick the minimum key vertex from the set of vertices not yet included in MST
let u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the adjacent vertices of the picked vertex.
for (let v = 0; v < V; v++) {
// graph[u][v] is non-zero only for adjacent vertices of u
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && !mstSet[v] && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
// Print the constructed MST
printMST(parent, graph);
}
// Driver code
let graph = [
[ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ]
];
// Print the solution
primMST(graph);
# A Python3 program for
# Prim's Minimum Spanning Tree (MST) algorithm.
# The program is for adjacency matrix
# representation of the graph
# Library for INT_MAX
import sys
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
# A utility function to print
# the constructed MST stored in parent[]
def printMST(self, parent):
print("Edge \tWeight")
for i in range(1, self.V):
print(parent[i], "-", i, "\t", self.graph[parent[i]][i])
# A utility function to find the vertex with
# minimum distance value, from the set of vertices
# not yet included in shortest path tree
def minKey(self, key, mstSet):
# Initialize min value
min = sys.maxsize
for v in range(self.V):
if key[v] < min and mstSet[v] == False:
min = key[v]
min_index = v
return min_index
# Function to construct and print MST for a graph
# represented using adjacency matrix representation
def primMST(self):
# Key values used to pick minimum weight edge in cut
key = [sys.maxsize] * self.V
parent = [None] * self.V # Array to store constructed MST
# Make key 0 so that this vertex is picked as first vertex
key[0] = 0
mstSet = [False] * self.V
parent[0] = -1 # First node is always the root of
for cout in range(self.V):
# Pick the minimum distance vertex from
# the set of vertices not yet processed.
# u is always equal to src in first iteration
u = self.minKey(key, mstSet)
# Put the minimum distance vertex in
# the shortest path tree
mstSet[u] = True
# Update dist value of the adjacent vertices
# of the picked vertex only if the current
# distance is greater than new distance and
# the vertex in not in the shortest path tree
for v in range(self.V):
# graph[u][v] is non zero only for adjacent vertices of m
# mstSet[v] is false for vertices not yet included in MST
# Update the key only if graph[u][v] is smaller than key[v]
if self.graph[u][v] > 0 and mstSet[v] == False \
and key[v] > self.graph[u][v]:
key[v] = self.graph[u][v]
parent[v] = u
self.printMST(parent)
# Driver's code
if __name__ == '__main__':
g = Graph(5)
g.graph = [[0, 2, 0, 6, 0],
[2, 0, 3, 8, 5],
[0, 3, 0, 0, 7],
[6, 8, 0, 0, 9],
[0, 5, 7, 9, 0]]
g.primMST()
Output: Shortest Path Distance Matrix
3 0 1 4 6
2 6 0 3 5
3 7 1 0 2
1 5 5 4 0
Each number represents the shortest distance from the row node to the column node after applying the Floyd-Warshall algorithm.
Time Complexity
The algorithm runs in O(V³) time, where V is the number of vertices. This complexity arises from three nested loops, each iterating over all vertices.
Auxiliary Space
The space complexity is O(1) beyond the input distance matrix, as the algorithm updates the matrix in place without requiring additional significant storage.
Note
The above implementation of the Floyd-Warshall algorithm only computes and prints the shortest distances between all pairs of nodes.
If you want to also reconstruct and print the actual shortest paths, the algorithm can be modified by maintaining a predecessor matrix (or parent matrix). This separate 2D matrix stores the predecessor of each node on the shortest path, allowing you to trace back the path from the destination node to the source node.
Real-World Applications of the Floyd-Warshall Algorithm
1. Network Routing in Computer Networking
The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.
2. Flight Connectivity in Aviation
In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.
3. Geographic Information Systems (GIS)
GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.
4. Kleene’s Algorithm and Formal Language Theory
A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.
Network Routing in Computer Networking
The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.
Flight Connectivity in Aviation
In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.
Geographic Information Systems (GIS)
GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.
Kleene’s Algorithm and Formal Language Theory
A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.
Edge Weight
0 – 1 2
1 – 2 3
0 – 3 6
1 – 4 5
Time Complexity: O(V²)
This complexity arises when the graph is represented using an adjacency matrix. However, when using an adjacency list and implementing a binary heap (priority queue), the time complexity of Prim’s Algorithm improves significantly to:
Optimized Time Complexity: O((E + V) * log V)
Auxiliary Space: O(V)
Optimized Implementation Using Adjacency List and Priority Queue
To enhance the efficiency of Prim’s Algorithm, we can use an adjacency list representation of the graph combined with a priority queue (or min-heap). Here’s a step-by-step explanation of the optimized approach:
- Convert the adjacency matrix into an adjacency list:
- Use ArrayList<ArrayList<Integer>> in Java,
- A list of lists in Python,
- Or an array of vectors in C++.
- Create a Pair class or structure to store each vertex along with its edge weight.
- Sort the adjacency list based on the edge weights, ensuring that lighter edges are considered first.
- Initialize a priority queue (min-heap) and push the starting vertex with its weight into the queue.
- Traverse the graph:
- At each step, pick the vertex with the lowest weight edge from the queue.
- Update adjacent vertices if a lower weight edge is found.
- Accumulate the minimum weights in a variable called ans.
After all vertices are processed, return the accumulated weight stored in ans as the total weight of the Minimum Spanning Tree (MST).
#include<bits/stdc++.h>
using namespace std;
// Function to find sum of weights of edges of the Minimum Spanning Tree.
int spanningTree(int V, int E, vector<vector<int>> &edges) {
// Create an adjacency list representation of the graph
vector<vector<int>> adj[V];
// Fill the adjacency list with edges and their weights
for (int i = 0; i < E; i++) {
int u = edges[i][0];
int v = edges[i][1];
int wt = edges[i][2];
adj[u].push_back({v, wt});
adj[v].push_back({u, wt});
}
// Create a priority queue to store edges with their weights
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
// Create a visited array to keep track of visited vertices
vector<bool> visited(V, false);
// Variable to store the result (sum of edge weights)
int res = 0;
// Start with vertex 0
pq.push({0, 0});
// Perform Prim's algorithm to find the Minimum Spanning Tree
while(!pq.empty()){
auto p = pq.top();
pq.pop();
int wt = p.first; // Weight of the edge
int u = p.second; // Vertex connected to the edge
if(visited[u] == true){
continue; // Skip if the vertex is already visited
}
res += wt; // Add the edge weight to the result
visited[u] = true; // Mark the vertex as visited
// Explore the adjacent vertices
for(auto v : adj[u]){
// v[0] represents the vertex and v[1] represents the edge weight
if(visited[v[0]] == false){
pq.push({v[1], v[0]}); // Add the adjacent edge to the priority queue
}
}
}
return res; // Return the sum of edge weights of the Minimum Spanning Tree
}
int main() {
vector<vector<int>> graph = {{0, 1, 5},
{1, 2, 3},
{0, 2, 1}};
cout << spanningTree(3, 3, graph) << endl;
return 0;
}
// A Java program for Prim's Minimum Spanning Tree (MST)
// algorithm. The program is for adjacency list
// representation of the graph
import java.io.*;
import java.util.*;
// Class to form pair
class Pair implements Comparable<Pair>
{
int v;
int wt;
Pair(int v,int wt)
{
this.v=v;
this.wt=wt;
}
public int compareTo(Pair that)
{
return this.wt-that.wt;
}
}
class GFG {
// Function of spanning tree
static int spanningTree(int V, int E, int edges[][])
{
ArrayList<ArrayList<Pair>> adj=new ArrayList<>();
for(int i=0;i<V;i++)
{
adj.add(new ArrayList<Pair>());
}
for(int i=0;i<edges.length;i++)
{
int u=edges[i][0];
int v=edges[i][1];
int wt=edges[i][2];
adj.get(u).add(new Pair(v,wt));
adj.get(v).add(new Pair(u,wt));
}
PriorityQueue<Pair> pq = new PriorityQueue<Pair>();
pq.add(new Pair(0,0));
int[] vis=new int[V];
int s=0;
while(!pq.isEmpty())
{
Pair node=pq.poll();
int v=node.v;
int wt=node.wt;
if(vis[v]==1)
continue;
s+=wt;
vis[v]=1;
for(Pair it:adj.get(v))
{
if(vis[it.v]==0)
{
pq.add(new Pair(it.v,it.wt));
}
}
}
return s;
}
// Driver code
public static void main (String[] args) {
int graph[][] = new int[][] {{0,1,5},
{1,2,3},
{0,2,1}};
// Function call
System.out.println(spanningTree(3,3,graph));
}
}
class PriorityQueue {
constructor() {
this.heap = [];
}
enqueue(value) {
this.heap.push(value);
let i = this.heap.length - 1;
while (i > 0) {
let j = Math.floor((i - 1) / 2);
if (this.heap[i][0] >= this.heap[j][0]) {
break;
}
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
i = j;
}
}
dequeue() {
if (this.heap.length === 0) {
throw new Error("Queue is empty");
}
let i = this.heap.length - 1;
const result = this.heap[0];
this.heap[0] = this.heap[i];
this.heap.pop();
i--;
let j = 0;
while (true) {
const left = j * 2 + 1;
if (left > i) {
break;
}
const right = left + 1;
let k = left;
if (right <= i && this.heap[right][0] < this.heap[left][0]) {
k = right;
}
if (this.heap[j][0] <= this.heap[k][0]) {
break;
}
[this.heap[j], this.heap[k]] = [this.heap[k], this.heap[j]];
j = k;
}
return result;
}
get count() {
return this.heap.length;
}
}
function spanningTree(V, E, edges) {
// Create an adjacency list representation of the graph
const adj = new Array(V).fill(null).map(() => []);
// Fill the adjacency list with edges and their weights
for (let i = 0; i < E; i++) {
const [u, v, wt] = edges[i];
adj[u].push([v, wt]);
adj[v].push([u, wt]);
}
// Create a priority queue to store edges with their weights
const pq = new PriorityQueue();
// Create a visited array to keep track of visited vertices
const visited = new Array(V).fill(false);
// Variable to store the result (sum of edge weights)
let res = 0;
// Start with vertex 0
pq.enqueue([0, 0]);
// Perform Prim's algorithm to find the Minimum Spanning Tree
while (pq.count > 0) {
const p = pq.dequeue();
const wt = p[0]; // Weight of the edge
const u = p[1]; // Vertex connected to the edge
if (visited[u]) {
continue; // Skip if the vertex is already visited
}
res += wt; // Add the edge weight to the result
visited[u] = true; // Mark the vertex as visited
// Explore the adjacent vertices
for (const v of adj[u]) {
// v[0] represents the vertex and v[1] represents the edge weight
if (!visited[v[0]]) {
pq.enqueue([v[1], v[0]]); // Add the adjacent edge to the priority queue
}
}
}
return res; // Return the sum of edge weights of the Minimum Spanning Tree
}
// Example usage
const graph = [[0, 1, 5], [1, 2, 3], [0, 2, 1]];
// Function call
console.log(spanningTree(3, 3, graph));
def tree(V, E, edges):
# Create an adjacency list representation of the graph
adj = [[] for _ in range(V)]
# Fill the adjacency list with edges and their weights
for i in range(E):
u, v, wt = edges[i]
adj[u].append((v, wt))
adj[v].append((u, wt))
# Create a priority queue to store edges with their weights
pq = []
# Create a visited array to keep track of visited vertices
visited = [False] * V
# Variable to store the result (sum of edge weights)
res = 0
# Start with vertex 0
heapq.heappush(pq, (0, 0))
# Perform Prim's algorithm to find the Minimum Spanning Tree
while pq:
wt, u = heapq.heappop(pq)
if visited[u]:
continue
# Skip if the vertex is already visited
res += wt
# Add the edge weight to the result
visited[u] = True
# Mark the vertex as visited
# Explore the adjacent vertices
for v, weight in adj[u]:
if not visited[v]:
heapq.heappush(pq, (weight, v))
# Add the adjacent edge to the priority queue
return res
# Return the sum of edge weights of the Minimum Spanning Tree
if __name__ == "__main__":
graph = [[0, 1, 5],
[1, 2, 3],
[0, 2, 1]]
# Function call
print(tree(3, 3, graph))
Output
4
Time Complexity: O((E + V) * log(V))
Where V is the number of vertices and E is the number of edges in the graph.
Auxiliary Space: O(E + V)
This space is used to store the graph and auxiliary data structures like the priority queue and visited array.
Advantages and Disadvantages of Prim’s Algorithm
Advantages:
- Guaranteed to find the MST: Prim’s algorithm reliably computes the Minimum Spanning Tree in any connected, weighted graph.
- Efficient with optimized data structures: When used with a binary heap or Fibonacci heap, it achieves a time complexity of O((E + V) * log(V)).
- Ease of understanding and implementation: Compared to some other MST algorithms, Prim’s algorithm is relatively straightforward to grasp and code.
Disadvantages:
- Performance on dense graphs: On graphs with a high number of edges, the algorithm may be slower since it needs to consider every edge at least once.
- Additional memory usage: The reliance on a priority queue can increase memory consumption, which might lead to slower performance on very large-scale graphs.
- MST may vary based on the starting node: The initial vertex selection can influence the structure of the resulting MST, which could be undesirable in certain scenarios where consistency is critical.
Note: If you’re studying Data Structures & Algorithms (DSA) for the first time, you can explore our comprehensive Data Structures & Algorithms course. For developers looking to build end-to-end applications, our Web Development program covers both frontend and backend concepts. If you want an integrated path covering algorithms, web development, and system design, check out the Master DSA, Web Dev & System Design curriculum. For those interested in analytics, our Data Science course offers hands-on projects and real-world datasets.
Network Routing in Computer Networking
The Floyd-Warshall algorithm is widely used in computer networks to determine the shortest paths between all pairs of nodes. This helps in efficient routing of data packets, ensuring optimal communication paths in network infrastructure.
Flight Connectivity in Aviation
In the aviation industry, this algorithm assists in finding the shortest and most cost-effective routes between airports, optimizing flight paths and connections for passengers and cargo.
Geographic Information Systems (GIS)
GIS applications frequently analyze spatial data such as road networks. Floyd-Warshall is used to calculate the shortest paths between various locations, helping in navigation, urban planning, and resource management.
Kleene’s Algorithm and Formal Language Theory
A generalization of Floyd-Warshall, known as Kleene’s algorithm, is employed in automata theory to compute regular expressions for regular languages, facilitating pattern matching and compiler design.
What is the main difference between Kruskal’s and Prim’s algorithms?
Kruskal’s algorithm is edge-centric, sorting all edges first and picking the smallest one that doesn’t form a cycle; Prim’s is vertex-centric, growing a tree from a starting vertex by adding the smallest edge connecting to the tree. If you prefer structured, step-by-step guidance on spanning tree algorithms, check out our DSA Course for expert-led tutorials.
How does Union-Find (DSU) speed up cycle detection in Kruskal’s Algorithm?
By keeping track of connected components in a tree-like structure. Each find operation locates the root parent of a vertex (compressing paths along the way), and union merges two components by rank. This nearly constant-time check avoids expensive cycle detection via traversal. If you want to see DSU and other algorithmic fundamentals applied in web-based projects, explore our Web Development Course.
Can Kruskal’s Algorithm handle graphs with negative edge weights?
Yes—since Kruskal’s sorts edges by weight, it will include negative-weight edges first (if they don’t create a cycle). The algorithm still produces the MST correctly, even if some edge weights are negative. For comprehensive practice problems on graph algorithms, consider enrolling in our Design DSA Combined program.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Essentials of Machine Learning and Artificial Intelligence
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 22+ Hands-on Live Projects & Deployments
- Comprehensive Notes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 57% OFF
₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 60% OFF
₹25,000.00 ₹9,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 65% OFF
₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 60% OFF
₹15,000.00 ₹5,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085
