Data Structures and Algorithms

DSA Interview Questions

Recursion and Backtracking: Basics and Applications

Want to master recursion and backtracking? These concepts are the backbone of solving complex programming challenges, from algorithm design to coding interviews. Whether you’re preparing for a tech role or sharpening your problem-solving skills, understanding these techniques is essential. Stay ahead of the curve by signing up for free course updates and exclusive resources tailored to help you excel.

Basics of Recursion

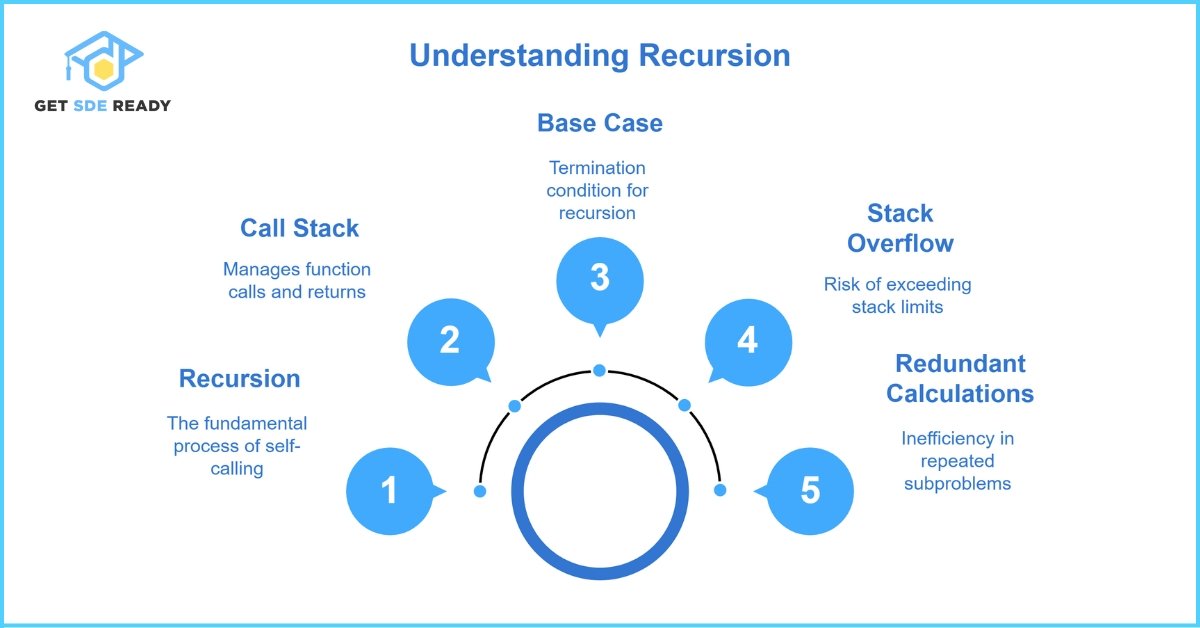
Recursion is a programming technique where a function calls itself to solve smaller instances of the same problem. Think of it like a Russian doll: each doll opens to reveal a smaller version until you reach the tiniest one.

What Makes Recursion Work?

Base Case: The stopping condition that prevents infinite loops.
Recursive Case: The part where the function calls itself with modified inputs.

For example, calculating a factorial:

def factorial(n):

if n == 0: # Base case

return 1

else: # Recursive case

return n * factorial(n-1)

Key Elements of Recursion

Divide and Conquer: Break problems into smaller subproblems.
Stack Utilization: Recursion uses the call stack to manage function calls.

Recursion vs. Iteration

– Recursion simplifies code but risks stack overflow.

– Iteration uses loops and is memory-efficient.

How Recursion Works

When a recursive function runs, each call gets added to the call stack. Once the base case is met, the stack “unwinds,” returning results backward.

Visualizing the Call Stack

Imagine solving a maze: you mark each path you take, backtracking if you hit a dead end. Similarly, the call stack tracks every recursive step.

Common Pitfalls

Stack Overflow: Occurs with deep recursion (e.g., factorial(10000)).
Redundant Calculations: Repeatedly solving the same subproblem (e.g., Fibonacci recursion).

For a deeper dive into managing recursion efficiently, explore advanced DSA strategies.

Basics of Backtracking

Backtracking is a refined form of recursion used to explore all possible solutions by building candidates incrementally and abandoning paths that don’t work (“pruning”).

Why Backtracking Matters

Solves constraint satisfaction problems (e.g., Sudoku, N-Queens).
Tests partial solutions and backtracks upon failure.

Characteristics of Backtracking

Incremental Construction: Build solutions step-by-step.
Pruning: Discard invalid paths early.

Recursion vs. Backtracking

– Recursion solves subproblems independently.

– Backtracking explores paths and reverses decisions.

How Backtracking Works

Backtracking follows a systematic approach:

Choose: Pick a potential candidate.
Explore: Recursively check if it leads to a solution.
Unchoose: Remove the candidate if it fails.

Example: Permutations

def backtrack(path, choices):
if solution_found:
    return path
for choice in choices:
    if valid(choice):
        path.append(choice)
        result = backtrack(path, remaining_choices)
        if result: return result
        path.pop()
return None

Key Differences Between Recursion and Backtracking

Aspect	Recursion	Backtracking
Purpose	Solve subproblems	Explore all possible solutions
Efficiency	Can be inefficient	Optimized via pruning
Use Cases	Tree traversals, Divide & Conquer	Puzzles, Optimization problems

Applications of Recursion and Backtracking

Real-World Uses

Recursion: File system traversal, Merge Sort, Tree/Graph algorithms.
Backtracking: Sudoku solvers, Robot path planning, Combinatorial problems.

Industry Applications

– AI: Pathfinding in robotics.

– Bioinformatics: DNA sequence alignment.

For hands-on practice, check out our comprehensive web development course that integrates DSA with real-world projects.

Common Problems and Solutions

Recursion Challenges

Stack Overflow: Solve using iteration or memoization.
Redundant Calls: Use dynamic programming to cache results.

Backtracking Challenges

Inefficient Pruning: Optimize constraint checks.
Combinatorial Explosion: Limit depth-first search.

Problem	Solution
Exponential time complexity	Memoization or iterative DP
Memory overuse	Tail recursion optimization

Best Practices and Optimization Techniques

Memoization: Cache results to avoid recomputation.
Tail Recursion: Convert recursive calls to loops.
Pruning Heuristics: Eliminate invalid paths early.

Tip: Always define clear base cases and constraints. Struggling with system design? Our DSA and Web Development combo course covers these optimizations in depth.

How do I decide between recursion and backtracking?

Use recursion for problems with overlapping subproblems (e.g., Fibonacci). Backtracking suits scenarios requiring exhaustive search (e.g., permutations). For structured learning, enroll in our Design and DSA Combined Course.

What’s the biggest mistake beginners make?

Neglecting the base case, leading to infinite loops. Always test edge cases first.

Are these concepts used in coding interviews?

Absolutely! Companies like Google and Meta frequently test recursion and backtracking. Prepare with our Data Science and Algorithm Guide.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

arun@getsdeready.com

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085