Data Structures and Algorithms

DSA Interview Questions

Segment Tree in Data Structure (Explained with Examples)

Introduction

The Segment Tree is a powerful data structure widely used in computer science, especially in competitive programming and software development. It allows for efficient range queries and updates on arrays, making it an essential tool for optimizing operations. In this guide, we’ll explore the fundamentals, advantages, and real-world applications of the Segment Tree in data structures.

What is a Segment Tree?

A Segment Tree is a binary tree-based data structure designed to perform range-based operations such as sum, minimum, maximum, and more, in a highly efficient way.
Consider a scenario where you have an array of numbers and you need to frequently:

Calculate the sum between two indices, or
Update a specific element in the array.

A Segment Tree helps execute these tasks in logarithmic time complexity (O(log n)), which is significantly faster than a brute-force approach. This efficiency makes it ideal for scenarios where performance is critical.

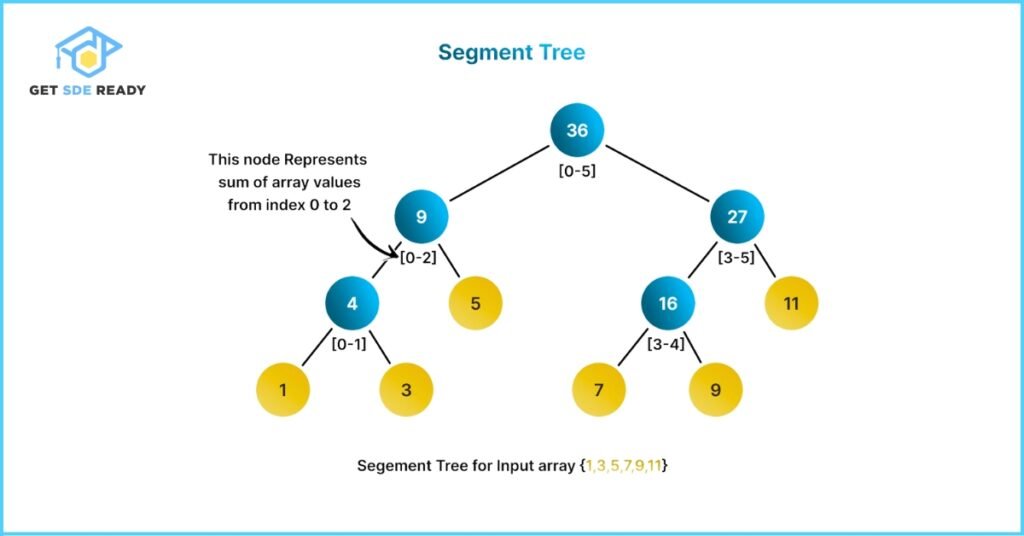
Structure of a Segment Tree

Root Node

The root node sits at the top of the tree and represents the entire range of the array. It holds information about the full list, such as the total sum or minimum value, depending on the operation.

Internal Nodes

These are the nodes between the root and the leaves. Internal nodes store information about sub-segments of the array. Each internal node represents a portion of the list and is built by combining the data from its child nodes.

Leaf Nodes

The leaf nodes represent the individual elements of the original array. These are the endpoints of the tree, and the building blocks used to compute the values in the internal and root nodes.

Each node essentially acts like a container that stores aggregated information (like sum, min, or max) for a particular segment of the array, allowing for quick and efficient access during queries or updates.

Real-World Analogies of Segment Tree

Bookshelf Sections

Imagine a long bookshelf filled with books. Instead of counting the pages of each book every time you need the total for a section, you divide the shelf into smaller parts and pre-calculate the total pages for each part.
Now, to find the total pages in a certain range, you simply combine the stored page counts from the relevant sections — much faster and easier.

Warehouse Inventory

Think of a warehouse with rows of shelves, each holding a number of items. If the manager wants to know how many items are stored across a specific range of shelves, they don’t have to count everything manually.
By keeping pre-recorded counts for each shelf segment, the manager can quickly retrieve and sum up the data — just like a Segment Tree does with numerical data.

Why Use the Segment Tree Data Structure?

Segment Trees are widely used in algorithm design because they provide optimized performance for operations that would otherwise be time-consuming. Here’s why they are so valuable:

Efficient Range Queries

Segment Trees enable fast computation of operations like sum, minimum, maximum, and more across a specific range of an array.
For example, if you’re frequently calculating the sum between two indices, a Segment Tree can return the result in O(log n) time — much faster than a traditional loop that takes O(n) time.

Fast Updates

Need to update an element in your array and immediately reflect that change in future queries? A Segment Tree handles this seamlessly.
When a value is modified, the tree automatically propagates the update to the necessary parent nodes, ensuring that subsequent queries remain accurate and fast.

Versatility

One of the greatest strengths of the Segment Tree is its adaptability. It can support a wide range of operations, such as:

Sum
Minimum / Maximum
Greatest Common Divisor (GCD)
Bitwise operations
This versatility makes it ideal for a variety of problem-solving scenarios in competitive programming and real-world applications.

Space Efficiency

While a Segment Tree uses more space than a plain array — roughly four times the size — it’s still quite efficient compared to other complex data structures.
For the benefits it provides in speed and flexibility, this trade-off in memory is usually well worth it.

If you want hands-on practice with these concepts, explore our DSA course for guided exercises and real-world problem sets.

How to Build a Segment Tree

Building a Segment Tree follows a systematic process. Here’s how it’s done:

1. Choose an Array

Start with your base array of numbers. For example:
[2, 4, 1, 3, 5]

2. Create the Leaf Nodes

Each leaf node in the tree corresponds to a single element of the array. So, for the given example, we will create five leaf nodes, one for each number.

3. Build the Internal Nodes

Next, pair up the leaf nodes and combine their values using the desired operation (like sum).
Each internal node will represent the result of its two child nodes. This process continues upward, forming the middle structure of the tree.

4. Repeat Until You Form the Root Node

Keep merging nodes until you build the root node, which holds the aggregated result for the entire array.
At this point, your Segment Tree is fully constructed and ready for efficient queries and updates.

Visual Representation of Segment Tree for Array [2, 4, 1, 3, 5]

To better understand how a Segment Tree is structured, let’s look at a visual example using the array:

				
					[2, 4, 1, 3, 5]

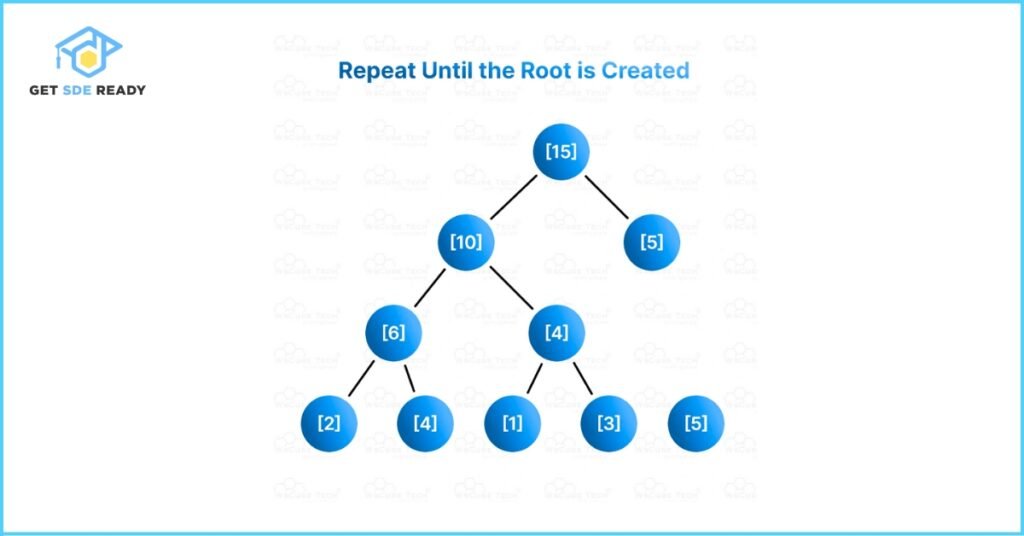
Segment Tree Operations

Segment Trees support two primary operations that make them highly useful for a variety of computational tasks: Query and Update. Below is a clear explanation of how each works.

Query Operation

The query operation in a Segment Tree retrieves information such as the sum, minimum, maximum, or other aggregate data from a specific range of the array — all with impressive speed.

Example:

Let’s refer back to our Segment Tree built from the array [2, 4, 1, 3, 5]. Suppose we want to find the sum of elements from index 1 to 3, which corresponds to the range [4, 1, 3].

Steps:

Start at the Root
The root node covers the entire range [0, 4].
Check for Overlap
- If the node’s range fully overlaps the query range, return the node’s value.
- If there is no overlap, return 0 (or a neutral value based on the operation type).
- If the overlap is partial, recursively explore both left and right children of the node.
Combine Results
Merge the results from the left and right subtrees to produce the final query result.

Update Operation

The update operation allows you to change a value in the original array and reflect that change in the Segment Tree, ensuring the tree remains accurate for future queries.

Example:

Let’s update the value at index 2 (which is 1) to 6 in the array [2, 4, 1, 3, 5].

Steps:

Start at the Root
Begin at the root node that represents the full range [0, 4].
Traverse to the Leaf
Navigate down the tree to find the leaf node corresponding to index 2.
Update the Leaf
Replace the old value with the new value (6) in the respective leaf node.
Update Internal Nodes
Move back up the tree, recalculating and updating the values of all parent nodes that include the modified element in their range.

This ensures that the Segment Tree continues to provide correct results for all range queries after any update — again in just O(log n) time.

Updated Segment Tree

After performing the update operation — changing the value at index 2 from 1 to 6 in the array [2, 4, 1, 3, 5] — the new array becomes:
[2, 4, 6, 3, 5]

As a result, the Segment Tree structure is modified to reflect this change. Here’s how the updated Segment Tree looks:

Segment Tree Implementation in Python, Java and C++

Understanding how to implement a Segment Tree in different programming languages helps solidify its concept and prepare you for real-world coding challenges. Below are practical code examples in Python, Java, and C++.

Segment Tree in Python

				
					#include <iostream>
#include <vector>

class SegmentTree {
private:
    std::vector<int> tree;
    int n;

    void build(const std::vector<int>& data) {
        for (int i = 0; i < n; i++)
            tree[n + i] = data[i];
        for (int i = n - 1; i > 0; --i)
            tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }

public:
    SegmentTree(const std::vector<int>& data) {
        n = data.size();
        tree.resize(2 * n);
        build(data);
    }

    void update(int idx, int value) {
        idx += n;
        tree[idx] = value;
        for (int i = idx; i > 1; i >>= 1)
            tree[i >> 1] = tree[i] + tree[i ^ 1];
    }

    int query(int l, int r) {
        int res = 0;
        l += n;
        r += n;
        while (l < r) {
            if (l & 1) res += tree[l++];
            if (r & 1) res += tree[--r];
            l >>= 1;
            r >>= 1;
        }
        return res;
    }
};

int main() {
    std::vector<int> data = {2, 4, 1, 3, 5};
    SegmentTree segTree(data);
    std::cout << segTree.query(1, 4) << std::endl;  // Output: 8
    segTree.update(2, 6);
    std::cout << segTree.query(1, 4) << std::endl;  // Output: 13
    return 0;
}

Searching

Traverse the loop to find a target value, requiring safeguards against infinite loops.

For a quick refresher on these operations, try our crash course.

Implementation of Circular Linked Lists

Let’s see how circular linked lists come to life in code. Below are examples in C, C++, and Java for inserting nodes at the beginning and end.

				
					class SegmentTree {
    private int[] tree;
    private int n;

    public SegmentTree(int[] data) {
        this.n = data.length;
        this.tree = new int[2 * n];
        build(data);
    }

    private void build(int[] data) {
        for (int i = 0; i < n; i++)
            tree[n + i] = data[i];
        for (int i = n - 1; i > 0; --i)
            tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }

    public void update(int idx, int value) {
        idx += n;
        tree[idx] = value;
        for (int i = idx; i > 1; i >>= 1)
            tree[i >> 1] = tree[i] + tree[i ^ 1];
    }

    public int query(int l, int r) {
        int res = 0;
        l += n;
        r += n;
        while (l < r) {
            if ((l & 1) == 1) res += tree[l++];
            if ((r & 1) == 1) res += tree[--r];
            l >>= 1;
            r >>= 1;
        }
        return res;
    }

    public static void main(String[] args) {
        int[] data = {2, 4, 1, 3, 5};
        SegmentTree segTree = new SegmentTree(data);
        System.out.println(segTree.query(1, 4));  // Output: 8
        segTree.update(2, 6);
        System.out.println(segTree.query(1, 4));  // Output: 13

				
					class SegmentTree:
    def __init__(self, data):
        self.n = len(data)
        self.tree = [0] * (2 * self.n)
        self.build(data)

    def build(self, data):
        for i in range(self.n):
            self.tree[self.n + i] = data[i]
        for i in range(self.n - 1, 0, -1):
            self.tree[i] = self.tree[i * 2] + self.tree[i * 2 + 1]

    def update(self, idx, value):
        idx += self.n
        self.tree[idx] = value
        i = idx
        while i > 1:
            self.tree[i // 2] = self.tree[i] + self.tree[i ^ 1]
            i //= 2

    def query(self, l, r):
        res = 0
        l += self.n
        r += self.n
        while l < r:
            if l & 1:
                res += self.tree[l]
                l += 1
            if r & 1:
                r -= 1
                res += self.tree[r]
            l //= 2
            r //= 2
        return res

# Example Usage
data = [2, 4, 1, 3, 5]
seg_tree = SegmentTree(data)
print(seg_tree.query(1, 4))  # Output: 8
seg_tree.update(2, 6)
print(seg_tree.query(1, 4))  # Output: 13

Each of these code implementations demonstrates how a Segment Tree can be constructed, queried, and updated efficiently in different programming environments. This cross-language perspective is valuable for both academic learning and technical interviews.

Time and Space Complexity of Segment Tree

Understanding the efficiency of Segment Trees is crucial for choosing the right data structure for range query and update problems. Here’s a breakdown of the time and space complexities for various operations:

Complexity Table

Operation	Time Complexity	Space Complexity
Building Segment Tree	O(n)	O(n)
Query Operation	O(log n)	O(1)
Update Operation	O(log n)	O(1)

Explanation

Building the Tree: Takes linear time O(n) since each node (leaf and internal) is computed once.
Query Operation: Each query checks only the relevant branches of the tree, resulting in O(log n) time.
Update Operation: Similar to querying, updates traverse from the leaf to the root, taking O(log n) time.
Space Complexity: The tree uses O(n) space for storage, but individual queries and updates require only constant additional space O(1) during execution.

For broader system architecture insights (e.g., how to integrate such data structures into scalable backends), explore our Web Development course and advanced system design modules.

FAQs

How does a Segment Tree differ from a Binary Indexed Tree?

While both Segment Trees and Binary Indexed Trees (Fenwick Trees) are used for range queries and updates, Segment Trees are more flexible. Segment Trees can handle a wider variety of operations (like min, max, GCD, etc.), while Binary Indexed Trees are typically limited to operations like sum or prefix sums. Additionally, Segment Trees work well for both point and range updates, offering more control.

Can Segment Trees handle dynamic arrays?

Standard Segment Trees are built for static arrays, but advanced variations like Dynamic Segment Trees or Segment Trees with Lazy Propagation can handle dynamic ranges and updates efficiently. However, frequent insertions or deletions in the middle of the array may require rebuilding the tree.

Can Segment Trees be used for 2D range queries?

Yes, 2D Segment Trees are a more complex form of the standard Segment Tree that can handle two-dimensional data. These are useful in applications like image processing, matrix operations, and games involving grids. However, they require more memory and are more difficult to implement efficiently.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

[email protected]

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Segment Tree in Data Structure (Explained with Examples)

Introduction

What is a Segment Tree?

Structure of a Segment Tree

Root Node

Internal Nodes

Leaf Nodes

Real-World Analogies of Segment Tree

Bookshelf Sections

Warehouse Inventory

Why Use the Segment Tree Data Structure?

Efficient Range Queries

Fast Updates

Versatility

Space Efficiency

How to Build a Segment Tree

1. Choose an Array

2. Create the Leaf Nodes

3. Build the Internal Nodes

4. Repeat Until You Form the Root Node

Visual Representation of Segment Tree for Array [2, 4, 1, 3, 5]

Segment Tree Operations

Query Operation

Example:

Steps:

Update Operation

Example:

Steps:

Updated Segment Tree

Segment Tree Implementation in Python, Java and C++

Segment Tree in Python

Searching

Implementation of Circular Linked Lists

Time and Space Complexity of Segment Tree

Complexity Table

Explanation

FAQs

How does a Segment Tree differ from a Binary Indexed Tree?

Can Segment Trees handle dynamic arrays?

Can Segment Trees be used for 2D range queries?

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Essentials of Machine Learning and Artificial Intelligence

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Fast-Track to Full Spectrum Software Engineering

Buy for 57% OFF ₹35,000.00 ₹14,999.00

DSA, High & Low Level System Designs

Buy for 60% OFF ₹25,000.00 ₹9,999.00

Low & High Level System Design

Buy for 65% OFF ₹20,000.00 ₹6,999.00

Mastering Mern Stack (WEB DEVELOPMENT)

Buy for 60% OFF ₹15,000.00 ₹5,999.00

10 Day Google Interview Preparation Bootcamp

Reach Out Now

Contact Email

Phone Number

Our Location

Quick Links

Quick Links

Social Media

Master Your Interviews with Our Free Roadmap!

Hi Instagram Fam! Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam! Get a FREE Cheat Sheet on System Design

Loved Our YouTube Videos? Get a FREE Cheat Sheet on System Design.

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 57% OFF
₹35,000.00 ₹14,999.00

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Buy for 65% OFF
₹20,000.00 ₹6,999.00

Buy for 60% OFF
₹15,000.00 ₹5,999.00

Hi Instagram Fam!
Get a FREE Cheat Sheet on System Design.

Hi LinkedIn Fam!
Get a FREE Cheat Sheet on System Design