Data Structures and Algorithms

DSA Interview Questions

Top 30 DSA Questions to Crack Product-Based Company Interviews

Introduction

Data Structures and Algorithms (DSA) are fundamental to computer science and are critical for anyone aiming to secure a role at top product-based companies like Google, Amazon, Microsoft, and Facebook. These companies are known for their rigorous interview processes, which test your problem-solving skills, logical reasoning, and ability to write efficient code. Mastering DSA equips you to tackle complex problems, optimize solutions, and demonstrate a deep understanding of software development principles.

To stay ahead in your preparation, sign up for our exclusive offers and free resources by clicking here: Sign up here.

Understanding the Interview Process

The interview process for product-based companies typically involves multiple stages:

Online Assessment: Candidates solve coding problems on platforms like HackerRank or CodeSignal, testing basic DSA knowledge and coding proficiency.
Phone Screen: A technical phone interview where you may solve one or two coding problems, often related to arrays, strings, or linked lists.
On-Site Interviews: Multiple rounds with different interviewers, focusing on advanced DSA topics like trees, graphs, and dynamic programming, alongside system design and behavioral questions.
Final Round: Senior-level interviews may emphasize system design, scalability, or leadership skills.

DSA questions are a cornerstone of the coding rounds, assessing your ability to think algorithmically and write clean, efficient code.

Detailed Solutions for Top 30 Questions

Below are in-depth explanations and solution approaches for 30 frequently asked DSA questions, selected for their prevalence in interviews at top tech companies.

1. Two Sum (Arrays)

Problem: Given an array of integers and a target sum, return the indices of two numbers that add up to the target.
Concept: Tests hash map usage for efficient lookups.
Solution Approach: Iterate through the array, storing each number and its index in a hash map. For each number, check if (target – number) exists in the hash map. If found, return the current index and the stored index.
Time Complexity: O(n), where n is the array length.
Space Complexity: O(n) for the hash map.

2. Reverse a Linked List (Linked List)

Problem: Reverse a singly linked list.
Concept: Tests understanding of linked list manipulation.
Solution Approach: Use three pointers (prev, curr, next). For each node, save the next node, reverse the link to point to prev, and move forward.
Time Complexity: O(n), where n is the number of nodes.
Space Complexity: O(1).

3. Valid Parentheses (Stacks)

Problem: Given a string of parentheses, determine if it is valid.
Concept: Tests stack usage for balancing parentheses.
Solution Approach: Push opening parentheses onto a stack. For each closing parenthesis, check if the stack’s top matches. If not, or if the stack is empty, return false. Ensure the stack is empty at the end.
Time Complexity: O(n), where n is the string length.
Space Complexity: O(n).

4. Merge K Sorted Lists (Linked List)

Problem: Merge k sorted linked lists into one sorted list.
Concept: Tests priority queue usage for merging.
Solution Approach: Use a min-heap to store the heads of the lists. Repeatedly pop the smallest node, add it to the result, and push the next node from the same list.
Time Complexity: O(N log k), where N is the total number of nodes, k is the number of lists.
Space Complexity: O(k).

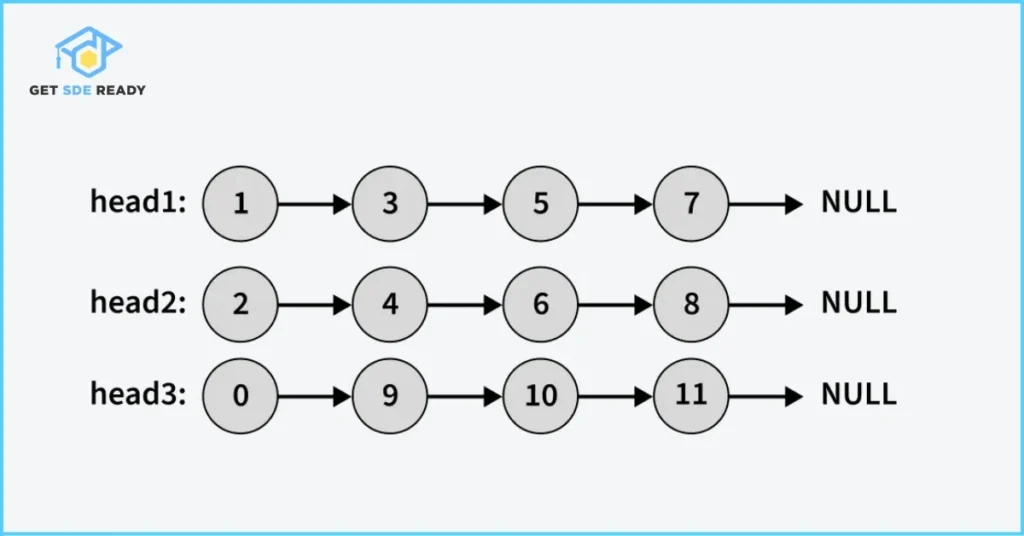
5. Maximum Depth of Binary Tree (Trees)

Problem: Find the maximum depth of a binary tree.
Concept: Tests recursive tree traversal.
Solution Approach: Use recursion to compute the depth of left and right subtrees, returning the maximum plus one.
Time Complexity: O(n), where n is the number of nodes.
Space Complexity: O(h), where h is the tree height.

6. Inorder Traversal of Binary Tree (Trees)

Problem: Perform an inorder traversal of a binary tree.
Concept: Tests tree traversal techniques.
Solution Approach: Recursively visit left subtree, current node, then right subtree. Alternatively, use a stack for iterative traversal.
Time Complexity: O(n).
Space Complexity: O(h).

7. Top K Frequent Elements (Heap)

Problem: Find the k most frequent elements in an array.
Concept: Tests heap and hash map usage.
Solution Approach: Count frequencies using a hash map, then use a min-heap of size k to keep track of the top k elements.
Time Complexity: O(n log k), where n is the array length.
Space Complexity: O(n).

8. Clone Graph (Graphs)

Problem: Clone an undirected graph.
Concept: Tests graph traversal and deep copying.
Solution Approach: Use DFS or BFS with a hash map to track cloned nodes, ensuring each node is copied only once.
Time Complexity: O(V + E), where V is vertices, E is edges.
Space Complexity: O(V).

9. Longest Substring Without Repeating Characters (Strings)

Problem: Find the length of the longest substring without repeating characters.
Concept: Tests sliding window technique.
Solution Approach: Use a hash map to store character indices and a sliding window to track the current substring.
Time Complexity: O(n).
Space Complexity: O(min(m, n)), where m is the character set size.

10. Regular Expression Matching (Dynamic Programming)

Problem: Implement regular expression matching with support for ‘.’ and ‘*’.
Concept: Tests dynamic programming for pattern matching.
Solution Approach: Use a DP table to track matching states between the string and pattern.
Time Complexity: O(m*n), where m and n are the lengths of the string and pattern.
Space Complexity: O(m*n).

11. Coin Change (Dynamic Programming)

Problem: Find the minimum number of coins needed to make a given amount.
Concept: Tests bottom-up dynamic programming.
Solution Approach: Use a DP array where dp[i] represents the minimum coins for amount i. Iterate through coins for each amount.
Time Complexity: O(amount * coins).
Space Complexity: O(amount).

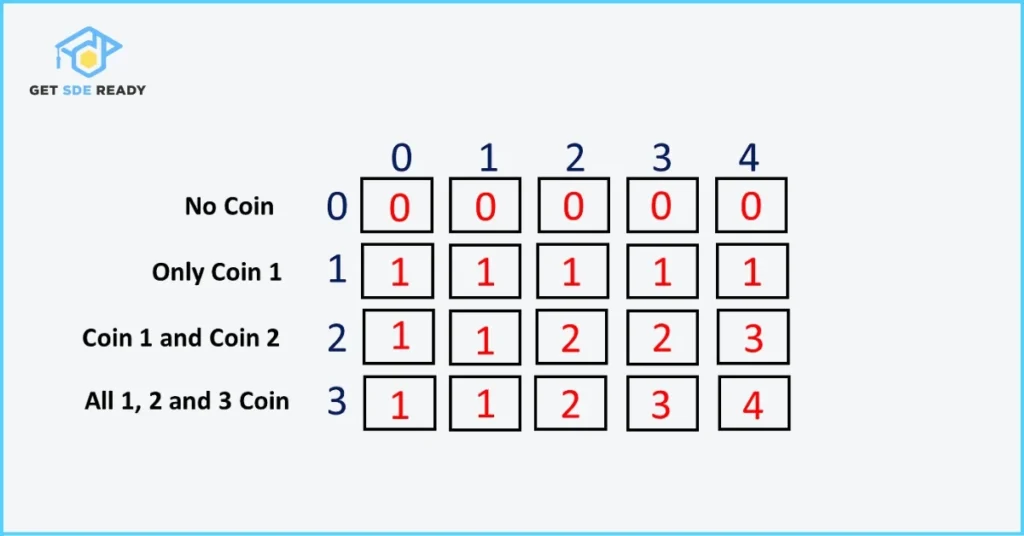
12. Word Break (Dynamic Programming)

Problem: Determine if a string can be segmented into words from a dictionary.
Concept: Tests dynamic programming for string segmentation.
Solution Approach: Use a DP array where dp[i] indicates if the substring up to i can be segmented. Check all prefixes.
Time Complexity: O(n^2).
Space Complexity: O(n).

13. Longest Increasing Subsequence (Dynamic Programming)

Problem: Find the length of the longest increasing subsequence in an array.
Concept: Tests dynamic programming for subsequences.
Solution Approach: Use a DP array where dp[i] stores the length of the LIS ending at index i.
Time Complexity: O(n^2).
Space Complexity: O(n).

14. Trapping Rain Water (Arrays)

Problem: Compute how much water can be trapped between bars of given heights.
Concept: Tests two-pointer technique.
Solution Approach: Use two pointers to track the maximum height from left and right, calculating trapped water at each index.
Time Complexity: O(n).
Space Complexity: O(1).

15. Container With Most Water (Arrays)

Problem: Find two lines that together with the x-axis form a container with the most water.
Concept: Tests two-pointer technique.
Solution Approach: Use two pointers starting from both ends, moving the pointer at the shorter line inward.
Time Complexity: O(n).
Space Complexity: O(1).

16. 3Sum (Arrays)

Problem: Find all unique triplets in an array that sum to zero.
Concept: Tests sorting and two-pointer technique.
Solution Approach: Sort the array, then for each element, use two pointers to find pairs summing to the negative of the element.
Time Complexity: O(n^2).
Space Complexity: O(1) or O(n) for sorting.

17. Letter Combinations of a Phone Number (Backtracking)

Problem: Given a string of digits, return all possible letter combinations.
Concept: Tests backtracking for combinatorial problems.
Solution Approach: Use recursion to build combinations by iterating through each

18. Spiral Matrix (Matrix)

Problem Statement: Given an m x n matrix, return all elements in spiral order (clockwise starting from the top-left).

Approach: Use four pointers (top, bottom, left, right) to track the boundaries of the matrix. Traverse the matrix in a spiral pattern: right, down, left, up, shrinking the boundaries after each traversal until they cross.

Solution Code:

				
					def spiralOrder(matrix):
    if not matrix:
        return []
    result = []
    top, bottom = 0, len(matrix) - 1
    left, right = 0, len(matrix[0]) - 1
    while top <= bottom and left <= right:
        # Traverse right
        for i in range(left, right + 1):
            result.append(matrix[top][i])
        top += 1
        # Traverse down
        for i in range(top, bottom + 1):
            result.append(matrix[i][right])
        right -= 1
        if top <= bottom:
            # Traverse left
            for i in range(right, left - 1, -1):
                result.append(matrix[bottom][i])
            bottom -= 1
        if left <= right:
            # Traverse up
            for i in range(bottom, top - 1, -1):
                result.append(matrix[i][left])
            left += 1
    return result

Time Complexity: O(m*n), where m and n are the dimensions of the matrix.
Space Complexity: O(1), excluding the output array.

19. Rotate Matrix (Matrix)

Problem Statement: Rotate an n x n matrix by 90 degrees clockwise in-place.

Approach: First, transpose the matrix (swap elements across the main diagonal). Then, reverse each row to achieve a 90-degree rotation.

Solution Code:

				
					def rotate(matrix):
    n = len(matrix)
    # Transpose matrix
    for i in range(n):
        for j in range(i, n):
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
    # Reverse each row
    for i in range(n):
        matrix[i].reverse()

Time Complexity: O(n^2), where n is the matrix size.
Space Complexity: O(1), as it’s done in-place.

20. Search in a row-wise and column-wise sorted matrix (Matrix)

Problem Statement: Given a matrix sorted row-wise and column-wise, find if a target element exists.

Approach: Start from the top-right corner. If the current element equals the target, return true. If it’s greater, move left; if smaller, move down.

Solution Code:

				
					def searchMatrix(matrix, target):
    if not matrix or not matrix[0]:
        return False
    m, n = len(matrix), len(matrix[0])
    row, col = 0, n - 1
    while row < m and col >= 0:
        if matrix[row][col] == target:
            return True
        elif matrix[row][col] > target:
            col -= 1
        else:
            row += 1
    return False

Time Complexity: O(m + n), where m and n are the matrix dimensions.
Space Complexity: O(1).

21. Longest Substring Without Repeating Characters (Strings)

Problem Statement: Find the length of the longest substring without repeating characters in a given string.

Approach: Use a sliding window with a hash map to track the last index of each character. Move the window’s start when a repeating character is found.

Solution Code:

				
					def lengthOfLongestSubstring(s):
    char_index = {}
    max_length = 0
    start = 0
    for end in range(len(s)):
        if s[end] in char_index and char_index[s[end]] >= start:
            start = char_index[s[end]] + 1
        else:
            max_length = max(max_length, end - start + 1)
        char_index[s[end]] = end
    return max_length

Time Complexity: O(n), where n is the string length.
Space Complexity: O(min(m, n)), where m is the character set size.

22. Check for Anagram (Strings)

Problem Statement: Determine if two strings are anagrams of each other.

Approach: Sort both strings and compare them, or use a frequency array to count characters.

Solution Code:

				
					def isAnagram(s, t):
    if len(s) != len(t):
        return False
    count = [0] * 26
    for c1, c2 in zip(s, t):
        count[ord(c1) - ord('a')] += 1
        count[ord(c2) - ord('a')] -= 1
    return all(c == 0 for c in count)

Time Complexity: O(n), where n is the string length.
Space Complexity: O(1), as the frequency array size is fixed.

23. Reverse words in a given string (Strings)

Problem Statement: Reverse the order of words in a given string.

Approach: Split the string into words, reverse the list of words, and join them back.

Solution Code:

				
					def reverseWords(s):
    words = s.strip().split()
    words.reverse()
    return ' '.join(words)

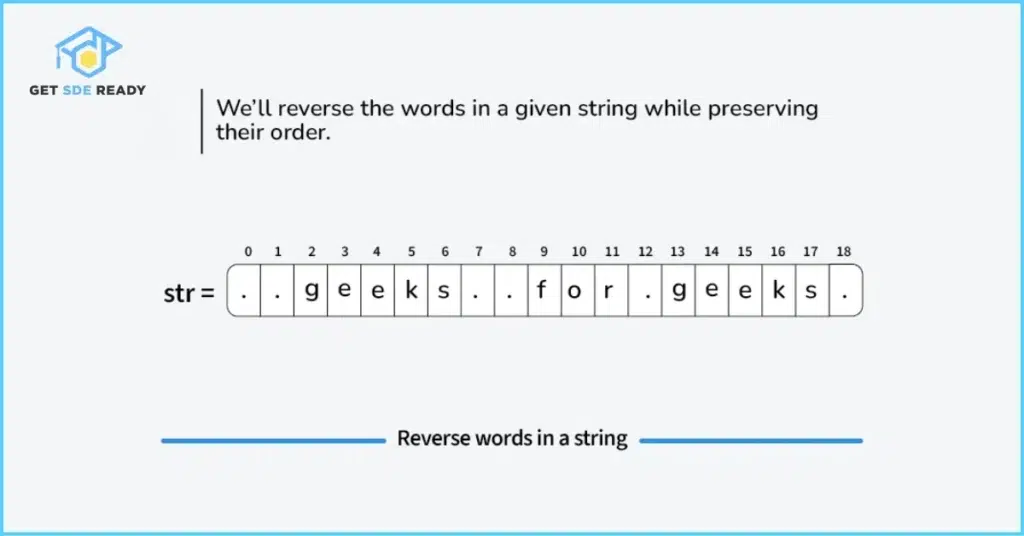
Time Complexity: O(n), where n is the string length.
Space Complexity: O(n), for storing the words.

24. Word Wrap Problem (Strings)

Problem Statement: Given a sequence of words and a maximum line width, wrap the words to minimize the total cost (sum of squares of extra spaces).

Approach: Use dynamic programming to compute the minimum cost for each prefix of the word list.

Solution Code:

				
					def wordWrap(words, k):
    n = len(words)
    dp = [float('inf')] * (n + 1)
    dp[0] = 0
    for i in range(1, n + 1):
        curr_len = -1
        for j in range(i, 0, -1):
            curr_len += len(words[j-1]) + 1
            if curr_len > k:
                break
            extra = k - curr_len + 1
            dp[i] = min(dp[i], dp[j-1] + extra * extra)
    return dp[n]

Time Complexity: O(n^2), where n is the number of words.
Space Complexity: O(n), for the DP array.

25. Implement atoi (Strings)

Problem Statement: Convert a string to an integer, handling signs, spaces, and overflow.

Approach: Parse the string, handle leading spaces, signs, and digits, and check for overflow.

Solution Code:

				
					def myAtoi(s):
    s = s.strip()
    if not s:
        return 0
    sign = 1
    if s[0] in ['+', '-']:
        sign = -1 if s[0] == '-' else 1
        s = s[1:]
    result = 0
    for c in s:
        if not c.isdigit():
            break
        result = result * 10 + int(c)
    result *= sign
    return max(min(result, 2**31 - 1), -2**31)

Time Complexity: O(n), where n is the string length.
Space Complexity: O(1).

26. Compare two strings represented as linked lists (Strings)

Problem Statement: Compare two strings where each character is a node in a linked list.

Approach: Traverse both linked lists simultaneously, comparing characters.

Solution Code:

				
					class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def compareStrings(list1, list2):
    while list1 and list2:
        if list1.val != list2.val:
            return False
        list1 = list1.next
        list2 = list2.next
    return list1 is None and list2 is None

Time Complexity: O(min(n, m)), where n and m are the lengths of the lists.
Space Complexity: O(1).

27. Find the first non-repeating character from a stream of characters (Strings)

Problem Statement: Find the first non-repeating character in a stream of characters.

Approach: Use a hash map to count character frequencies and a queue to track order.

Solution Code:

				
					from collections import deque

def firstNonRepeating(stream):
    count = {}
    queue = deque()
    for char in stream:
        count[char] = count.get(char, 0) + 1
        if count[char] == 1:
            queue.append(char)
        while queue and count[queue[0]] > 1:
            queue.popleft()
        print(queue[0] if queue else '#')

Time Complexity: O(n), where n is the stream length.
Space Complexity: O(k), where k is the character set size.

28. Count and Say Problem (Strings)

Problem Statement: Generate the nth term of the “count and say” sequence.

Approach: Iteratively generate each term by counting consecutive digits in the previous term.

Solution Code:

				
					def countAndSay(n):
    if n == 1:
        return "1"
    s = countAndSay(n - 1)
    result = ""
    count = 1
    for i in range(len(s)):
        if i == len(s) - 1 or s[i] != s[i + 1]:
            result += str(count) + s[i]
            count = 1
        else:
            count += 1
    return result

Time Complexity: O(2^n), due to exponential growth of the string.
Space Complexity: O(2^n), for storing the result.

29. Edit Distance (Strings)

Problem Statement: Compute the minimum number of operations (insert, delete, replace) to convert one string to another.

Approach: Use dynamic programming with a 2D table to store the minimum operations for substrings.

Solution Code:

				
					def minDistance(word1, word2):
    m, n = len(word1), len(word2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    for i in range(m + 1):
        dp[i][0] = i
    for j in range(n + 1):
        dp[0][j] = j
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if word1[i-1] == word2[j-1]:
                dp[i][j] = dp[i-1][j-1]
            else:
                dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
    return dp[m][n]

Time Complexity: O(mn), where m and n are the string lengths.
Space Complexity: O(mn), for the DP table.

30. Longest Palindromic Substring (Strings)

Problem Statement: Find the longest substring that is a palindrome.

Approach: Use the expand-around-center technique to check for palindromes centered at each position.

Solution Code:

				
					def longestPalindromicSubstring(s):
    def expand(left, right):
        while left >= 0 and right < len(s) and s[left] == s[right]:
            left -= 1
            right += 1
        return s[left + 1:right]
    
    longest = ""
    for i in range(len(s)):
        # Odd length palindromes
        palindrome1 = expand(i, i)
        if len(palindrome1) > len(longest):
            longest = palindrome1
        # Even length palindromes
        palindrome2 = expand(i, i + 1)
        if len(palindrome2) > len(longest):
            longest = palindrome2
    return longest

Time Complexity: O(n^2), where n is the string length.
Space Complexity: O(1), excluding the output string.

Preparation Tips

To excel in DSA interviews, consider the following:

Practice Regularly: Solve problems daily on platforms like LeetCode or HackerRank.
Understand Concepts: Focus on understanding the logic behind each solution.
Analyze Complexity: Be ready to explain time and space complexity during interviews.

DSA, High & Low Level System Designs

85+ Live Classes & Recordings
24*7 Live Doubt Support
400+ DSA Practice Questions
Comprehensive Notes
HackerRank Tests & Quizzes
Topic-wise Quizzes
Case Studies
Access to Global Peer Community

Buy for 60% OFF
₹25,000.00 ₹9,999.00

Accelerate your Path to a Product based Career

Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

Reach Out Now

If you have any queries, please fill out this form. We will surely reach out to you.

Contact Email

Reach us at the following email address.

arun@getsdeready.com

Phone Number

You can reach us by phone as well.

+91-97737 28034

Our Location

Rohini, Sector-3, Delhi-110085

Topic	Number of Questions	Example Questions
Arrays	16	Pair with the given Sum, Best Time to Buy and Sell Stock
Matrix	4	Set Matrix Zeroes, Spiral Matrix
Strings	10	Longest Substring Without Repeating Characters, Check for Anagram

Top 30 DSA Questions to Crack Product-Based Company Interviews

Introduction

Understanding the Interview Process