Data Structures and Algorithms
- Introduction to Data Structures and Algorithms
- Time and Space Complexity Analysis
- Big-O, Big-Theta, and Big-Omega Notations
- Recursion and Backtracking
- Divide and Conquer Algorithm
- Dynamic Programming: Memoization vs. Tabulation
- Greedy Algorithms and Their Use Cases
- Understanding Arrays: Types and Operations
- Linear Search vs. Binary Search
- Sorting Algorithms: Bubble, Insertion, Selection, and Merge Sort
- QuickSort: Explanation and Implementation
- Heap Sort and Its Applications
- Counting Sort, Radix Sort, and Bucket Sort
- Hashing Techniques: Hash Tables and Collisions
- Open Addressing vs. Separate Chaining in Hashing
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
DSA Interview Questions
- DSA Questions for Beginners
- Advanced DSA Questions for Competitive Programming
- Top 10 DSA Questions to Crack Your Next Coding Test
- Top 50 DSA Questions Every Programmer Should Practice
- Top Atlassian DSA Interview Questions
- Top Amazon DSA Interview Questions
- Top Microsoft DSA Interview Questions
- Top Meta (Facebook) DSA Interview Questions
- Netflix DSA Interview Questions and Preparation Guide
- Top 20 DSA Interview Questions You Need to Know
- Top Uber DSA Interview Questions and Solutions
- Google DSA Interview Questions and How to Prepare
- Airbnb DSA Interview Questions and How to Solve Them
- Mobile App DSA Interview Questions and Solutions
Introduction to High-Level System Design
System Design Fundamentals
- Functional vs. Non-Functional Requirements
- Scalability, Availability, and Reliability
- Latency and Throughput Considerations
- Load Balancing Strategies
Architectural Patterns
- Monolithic vs. Microservices Architecture
- Layered Architecture
- Event-Driven Architecture
- Serverless Architecture
- Model-View-Controller (MVC) Pattern
- CQRS (Command Query Responsibility Segregation)
Scaling Strategies
- Vertical Scaling vs. Horizontal Scaling
- Sharding and Partitioning
- Data Replication and Consistency Models
- Load Balancing Strategies
- CDN and Edge Computing
Database Design in HLD
- SQL vs. NoSQL Databases
- CAP Theorem and its Impact on System Design
- Database Indexing and Query Optimization
- Database Sharding and Partitioning
- Replication Strategies
API Design and Communication
Caching Strategies
- Types of Caching
- Cache Invalidation Strategies
- Redis vs. Memcached
- Cache-Aside, Write-Through, and Write-Behind Strategies
Message Queues and Event-Driven Systems
- Kafka vs. RabbitMQ vs. SQS
- Pub-Sub vs. Point-to-Point Messaging
- Handling Asynchronous Workloads
- Eventual Consistency in Distributed Systems
Security in System Design
Observability and Monitoring
- Logging Strategies (ELK Stack, Prometheus, Grafana)
- API Security Best Practices
- Secure Data Storage and Access Control
- DDoS Protection and Rate Limiting
Real-World System Design Case Studies
- Distributed locking (Locking and its Types)
- Memory leaks and Out of memory issues
- HLD of YouTube
- HLD of WhatsApp
System Design Interview Questions
- Adobe System Design Interview Questions
- Top Atlassian System Design Interview Questions
- Top Amazon System Design Interview Questions
- Top Microsoft System Design Interview Questions
- Top Meta (Facebook) System Design Interview Questions
- Top Netflix System Design Interview Questions
- Top Uber System Design Interview Questions
- Top Google System Design Interview Questions
- Top Apple System Design Interview Questions
- Top Airbnb System Design Interview Questions
- Top 10 System Design Interview Questions
- Mobile App System Design Interview Questions
- Top 20 Stripe System Design Interview Questions
- Top Shopify System Design Interview Questions
- Top 20 System Design Interview Questions
- Top Advanced System Design Questions
- Most-Frequented System Design Questions in Big Tech Interviews
- What Interviewers Look for in System Design Questions
- Critical System Design Questions to Crack Any Tech Interview
- Top 20 API Design Questions for System Design Interviews
- Top 10 Steps to Create a System Design Portfolio for Developers
Top 10 Recursion Problems and How to Break Them Down Efficiently
Introduction
Recursion is a powerful concept in computer science that enables us to solve complex problems by breaking them down into smaller, more manageable pieces. In this article, we will explore the top 10 recursion problems and explain how to efficiently break them down step by step. Whether you are a beginner or an experienced developer, understanding these recursion challenges will help you improve your problem-solving skills. Recursion is often compared to iterative approaches, yet it offers an elegant solution when used properly.
The concept of recursion can sometimes appear daunting, but with clear examples and systematic breakdowns, even a fifth grader can grasp its fundamentals. It’s important to recognize that every recursive solution has a base case and a recursive step. This method not only simplifies complex algorithms but also makes your code more readable and maintainable. For additional tips and techniques, exploring related topics like algorithm design and coding best practices is highly beneficial.
Also Read: Low-Level Design of YouTube Recommendations
1: Factorial Calculation
Factorial calculation is a classic example of recursion where the function calls itself with a decrementing number until it reaches 1. The factorial of a number nn (written as n!n!) is the product of all positive integers up to nn. This problem is an excellent starting point for understanding recursion because of its simple yet illustrative recursive nature.
In a recursive factorial function, the base case is when nn equals 1, and the recursive step multiplies nn by the factorial of n−1n-1. Many students and professionals alike use factorial recursion to learn how recursion unwinds and eventually resolves. The simplicity of this problem allows learners to focus on understanding the control flow and the importance of a base case.
Key Points:
- Base Case: n=1n = 1 or n=0n = 0
- Recursive Step: n!=n×(n−1)!n! = n \times (n-1)!
- Application: Widely used in combinatorics and probability calculations
Step | Description |
Base Case | When nn is 0 or 1 |
Recursive Case | Multiply nn by factorial of n−1n-1 |
This simple breakdown makes the factorial problem a perfect example for learning how recursion works and how to handle recursive calls efficiently. Experts often quote renowned computer scientists who emphasize that mastering recursion is fundamental for algorithm optimization.
Also Read: Top 10 DSA Questions on Linked Lists and Arrays
2: Fibonacci Sequence
The Fibonacci sequence is another popular recursion problem where each number is the sum of the two preceding ones, starting from 0 and 1. The recursive approach for generating Fibonacci numbers is straightforward, yet it is important to handle overlapping subproblems to improve efficiency. While the naive recursive solution can be inefficient, dynamic programming techniques such as memoization can significantly enhance performance.
In a recursive Fibonacci function, the base cases are defined when the sequence index is 0 or 1. The recursive case then computes the sum of the two previous Fibonacci numbers. It is a great example to understand the concept of overlapping subproblems and the benefits of caching previously computed results. Additionally, learning how to optimize recursive solutions is key to mastering more advanced algorithms.
Key Points:
- Base Cases: F(0)=0F(0) = 0, F(1)=1F(1) = 1
- Recursive Step: F(n)=F(n−1)+F(n−2)F(n) = F(n-1) + F(n-2)
- Optimization: Use memoization to reduce repeated computations
Index nn | Fibonacci Number F(n)F(n) |
0 | 0 |
1 | 1 |
2 | 1 |
3 | 2 |
4 | 3 |
By understanding and implementing the Fibonacci sequence recursively, developers can gain insights into both the power and limitations of recursion. This example also highlights the importance of identifying and optimizing overlapping subproblems in recursive algorithms.

3: Tower of Hanoi
The Tower of Hanoi is a classic puzzle that is frequently used to teach recursion and algorithmic thinking. The problem involves moving a stack of disks from one peg to another, following strict rules. This challenge requires you to move smaller sub-stacks recursively, ensuring that larger disks are never placed on top of smaller ones. The Tower of Hanoi is not only an exercise in recursion but also a demonstration of algorithmic efficiency.
In solving the Tower of Hanoi problem recursively, the base case occurs when there is only one disk to move. The recursive solution involves moving n−1n-1 disks to an auxiliary peg, moving the largest disk to the target peg, and then moving the n−1n-1 disks from the auxiliary peg to the target peg. This breakdown shows the power of recursion in solving problems that might initially seem unsolvable with iterative methods.
Key Points:
- Base Case: Single disk scenario
- Recursive Step: Move n−1n-1 disks, shift largest disk, then move n−1n-1 disks again
- Complexity: The number of moves required is 2n−12^n – 1
Number of Disks | Minimum Moves Required |
1 | 1 |
2 | 3 |
3 | 7 |
4 | 15 |
This problem is a favorite among educators for its clarity in demonstrating the recursive method. Statistically, the Tower of Hanoi problem is used in various computer science curriculums to illustrate the exponential growth in recursive function calls if not optimized properly.
Also Read: Top 10 System Design Interview Questions 2025
4: Permutations of a Set
Generating permutations is a common problem in computer science that can be elegantly solved with recursion. The goal is to list all possible arrangements of a set of items, and recursion simplifies this by breaking the problem into smaller subproblems. Each recursive call fixes one element and permutes the rest of the list, thereby covering all possible arrangements.
For permutation problems, the base case is reached when there is only one element left to arrange. The recursive case involves swapping elements and then recursively calling the function on the remaining list. This approach is highly intuitive and forms the backbone of many algorithms that require exploring all potential combinations.
Key Points:
- Base Case: A single element remains
- Recursive Step: Fix an element and recursively permute the rest
- Use Cases: Important in solving puzzles, optimization problems, and generating test cases
Step | Action |
1 | Choose an element |
2 | Swap with current position |
3 | Recurse for remaining elements |
4 | Backtrack to restore order |
By dissecting the permutation problem recursively, programmers can clearly see how complex arrangements emerge from simple recursive calls. This method also facilitates debugging and testing, making it easier to identify mistakes in logic or implementation.
Also Read: Why System Design Interviews Are Tough
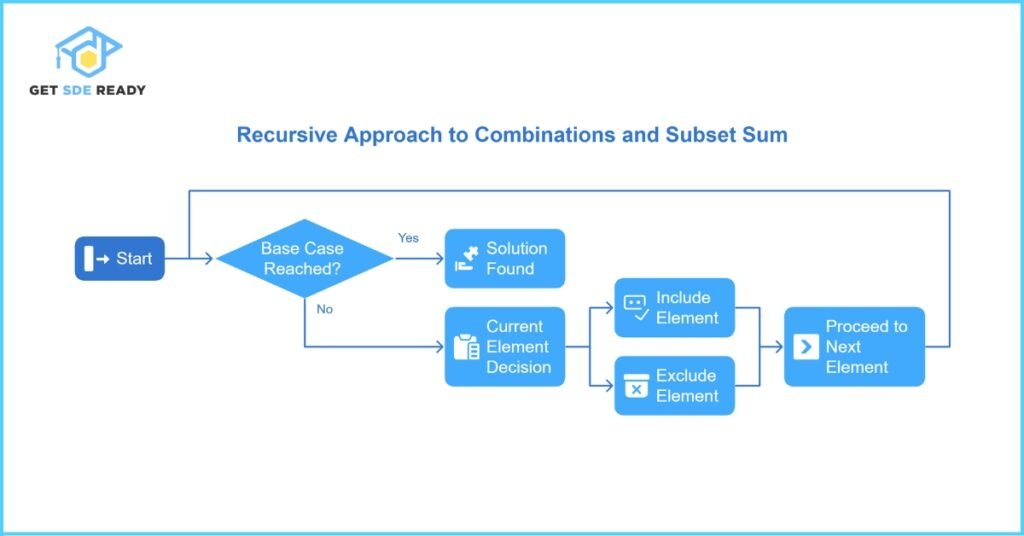
5: Combinations and Subset Sum
Recursion is not only useful for permutations but also for generating combinations and solving subset sum problems. The subset sum problem involves finding a subset of numbers that add up to a target sum, while the combinations problem requires selecting a specific number of elements from a set. Both of these problems can be efficiently tackled using recursion, as they involve exploring all possible selections of elements.
For these types of problems, the base case occurs when the subset is either empty or the desired number of elements has been chosen. The recursive approach involves either including the current element in the subset or excluding it, then proceeding to the next element. This dual-choice scenario is a hallmark of recursive solutions in combinatorial problems.
Key Points:
- Base Case: Target subset size reached or no elements remain
- Recursive Choice: Include or exclude the current element
- Applications: Useful in optimization, resource allocation, and decision-making processes
Decision | Outcome |
Include element | Add element and reduce target |
Exclude element | Move to the next element |
Base Condition | Subset meets criteria or no elements left |
This problem often serves as a gateway for learning advanced recursion techniques and dynamic programming. Experts have noted that mastering such combinatorial problems is critical for algorithm design, especially in interview settings and competitive programming.
6: Binary Search in a Sorted Array
Binary search is a fundamental algorithm that can be implemented using recursion to locate an element in a sorted array. The idea is to repeatedly divide the search interval in half, comparing the target value to the middle element of the array. If the target value is not found, the search continues in the appropriate half. Although binary search is often implemented iteratively, the recursive approach offers clarity in understanding divide-and-conquer techniques.
In the recursive binary search, the base case occurs when the search interval is empty, meaning the target is not present in the array. The recursive step involves calculating the midpoint and then determining whether to search the left or right half of the array. This method is both elegant and efficient, with a logarithmic time complexity of O(logn)O(\log n).
Key Points:
- Base Case: Array segment is empty
- Recursive Step: Compare target with middle element and decide direction
- Advantages: Simplifies the division of the search space and clarifies algorithm logic
Step | Process Description |
1 | Calculate the midpoint of the array |
2 | Compare the target with the midpoint value |
3 | Recurse on the appropriate half |
Binary search is a classic example of how recursion can simplify the logic behind dividing a problem space, making it a valuable tool in both academic and practical coding scenarios. Its efficiency and clarity have made it one of the most taught algorithms in computer science curricula worldwide.
Also Read: How to Crack DSA Interviews in 3 Months
7: Merge Sort Algorithm
Merge sort is a highly efficient, comparison-based sorting algorithm that employs recursion to break down arrays into smaller segments before merging them back together in sorted order. The divide-and-conquer strategy lies at the heart of merge sort, making it a perfect example of recursion in action. The algorithm splits the array recursively until each sub-array has one element, then merges these sub-arrays while sorting them.
In the merge sort algorithm, the base case is reached when the sub-array contains a single element. The recursive case involves dividing the array into two halves and then merging the sorted halves. This process ensures that at every step, the array becomes more organized until the entire array is sorted. The merge process itself requires careful handling to maintain the correct order, which can be implemented using additional temporary storage.
Key Points:
- Base Case: Sub-array with one element
- Recursive Division: Split array into halves repeatedly
- Merge Process: Combine sorted arrays into one
Phase | Description |
Division | Recursively split array into two halves |
Base Case | Single element arrays |
Merging | Combine and sort the halves |
Merge sort is celebrated for its predictable O(nlogn)O(n \log n) time complexity and its stable sorting characteristics. Many developers find that breaking down merge sort recursively not only clarifies the algorithm but also highlights the importance of managing memory and temporary data during the merge phase.
Also Read: Top 15 Full-Stack Dev Interview Questions 2025
8: Quick Sort Algorithm
Quick sort is another efficient sorting algorithm that uses recursion and the divide-and-conquer strategy. Unlike merge sort, quick sort works by selecting a pivot element from the array and partitioning the remaining elements into two sub-arrays based on whether they are less than or greater than the pivot. This partitioning step is key to the algorithm, as it positions the pivot in its correct place and allows the algorithm to recursively sort the sub-arrays.
The recursive quick sort function terminates when the sub-array has fewer than two elements, making the base case clear and concise. Although quick sort can have a worst-case time complexity of O(n2)O(n^2), the average complexity is O(nlogn)O(n \log n), which is why it is widely used in practical applications. With careful pivot selection, the performance of quick sort can be optimized to reduce the risk of encountering the worst-case scenario.
Key Points:
- Base Case: Sub-array has less than two elements
- Pivot Selection: Choose an element to partition the array
- Partitioning: Rearrange elements based on pivot comparison
Stage | Description |
Pivot Selection | Choose an element from the array |
Partitioning | Reorder array so that elements are partitioned by pivot |
Recursive Sort | Apply quick sort to the resulting sub-arrays |
Quick sort’s efficiency and in-place sorting capability make it a favorite in many software development scenarios. Its recursive structure simplifies the implementation of complex partitioning logic, which is a critical skill for developers facing algorithmic challenges.
Also Read: System Design for Real-Time Chat Apps
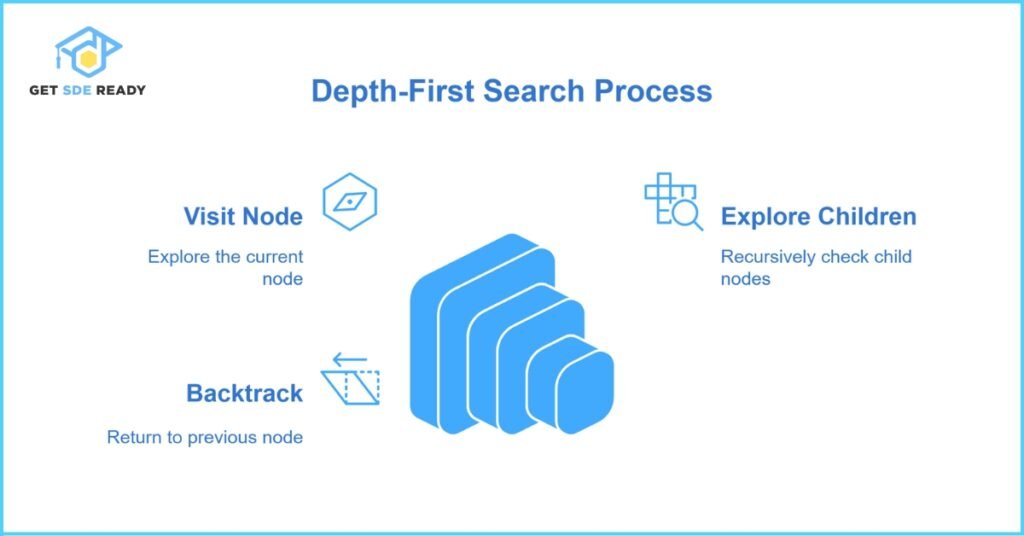
9: Depth-First Search (Tree Traversal)
Depth-first search (DFS) is a recursive algorithm used to traverse or search tree and graph data structures. DFS explores as far along each branch as possible before backtracking, making it an ideal candidate for recursive implementation. This method is particularly useful in scenarios such as maze solving, file system exploration, and analyzing network structures. The recursive approach makes the algorithm both elegant and straightforward.
In a DFS implementation, the base case is reached when there are no more child nodes to explore. The recursive case involves visiting a node, then recursively exploring each of its children before backtracking. This clear, structured approach helps in efficiently managing the traversal process while ensuring that every node is visited. It also demonstrates the effectiveness of recursion in handling hierarchical data structures.
Key Points:
- Base Case: A node with no children
- Recursive Step: Visit node and recursively explore its children
- Applications: Widely used in graph theory, game development, and AI pathfinding
Process | Description |
Visit Node | Process current node data |
Recurse on Child | Call DFS for each child node |
Backtrack | Return to previous node after child exploration |
Depth-first search is praised for its simplicity and clarity when implemented recursively. Its practical applications across various domains, from AI to network analysis, highlight the versatility of recursion in solving real-world problems.
Also Read: Top 10 Greedy Algorithms for Programming
10: Solving the N-Queens Problem
The N-Queens problem involves placing NN queens on an N×NN \times N chessboard such that no two queens threaten each other. This problem is a benchmark for testing recursive backtracking algorithms. By placing one queen at a time and ensuring no conflicts with previously placed queens, the problem naturally lends itself to a recursive solution that backtracks upon encountering conflicts.
In the N-Queens problem, the base case is reached when queens have been successfully placed in all rows. The recursive case involves placing a queen in a valid position on the current row and then calling the function recursively for the next row. If no valid position is found, the algorithm backtracks and tries a different position for the previous queen. This methodical approach showcases the importance of backtracking in recursive solutions and demonstrates how recursion can be used to explore large solution spaces systematically.
Key Points:
- Base Case: All queens are placed successfully
- Recursive Decision: Place a queen and move to the next row
- Backtracking: Revert decisions when a conflict is detected
Aspect | Description |
Valid Placement | Ensure no two queens threaten each other |
Recursive Call | Move to the next row after placement |
Backtracking | Remove queen if no valid positions are available |
The N-Queens problem is well-known in algorithm design for its complexity and the elegant recursive approach it necessitates. Learning this problem enhances one’s ability to handle other recursive challenges that require systematic exploration and backtracking.
Also Read: Top 10 Python Libraries and Frameworks
What is recursion and why is it important in programming?
Recursion is a method of solving problems where a function calls itself to break down the problem into simpler subproblems. It is important because it offers an elegant solution for complex challenges like tree traversals and combinatorial searches. Recursion simplifies code, improves readability, and is essential in many algorithms. For more insights on algorithm design, consider exploring our data structures course.
How can I optimize recursive algorithms for better performance?
Optimizing recursive algorithms can be achieved through techniques such as memoization, which caches previously computed results, and tail recursion, which minimizes the overhead of recursive calls. It is also important to ensure that every recursive function has a clearly defined base case to prevent infinite recursion. Efficient recursion not only improves runtime but also conserves memory, making your applications more robust. For additional optimization strategies, check out our web development course.
What common pitfalls should developers avoid when using recursion?
Developers should avoid common pitfalls such as missing or incorrect base cases, which can lead to infinite recursion, and excessive memory use due to deep recursive calls. Another common issue is not accounting for overlapping subproblems, which can make recursive solutions inefficient without proper optimization techniques like memoization. Understanding these pitfalls is crucial for writing effective and maintainable recursive code. To further improve your skills, explore our combined design and DSA course.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 52% OFF
₹25,000.00 ₹11,999.00
Accelerate your Path to a Product based Career
Boost your career or get hired at top product-based companies by joining our expertly crafted courses. Gain practical skills and real-world knowledge to help you succeed.

DSA, High & Low Level System Designs
- 85+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- Topic-wise Quizzes
- Case Studies
- Access to Global Peer Community
Buy for 52% OFF
₹25,000.00 ₹11,999.00

Fast-Track to Full Spectrum Software Engineering
- 120+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests & Quizzes
- 12+ live Projects & Deployments
- Case Studies
- Access to Global Peer Community
Buy for 51% OFF
₹35,000.00 ₹16,999.00

Low & High Level System Design
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- Case Studies
- Comprehensive Notes
- HackerRank Tests
- Topic-wise Quizzes
- Access to Global Peer Community
- Interview Prep Material
Buy for 60% OFF
₹20,000.00 ₹7,999.00

Mastering Mern Stack (WEB DEVELOPMENT)
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 12+ Hands-on Live Projects & Deployments
- Comprehensive Notes & Quizzes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 53% OFF
₹15,000.00 ₹6,999.00

Mastering Data Structures & Algorithms
- 65+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 400+ DSA Practice Questions
- Comprehensive Notes
- HackerRank Tests
- Access to Global Peer Community
- Topic-wise Quizzes
- Interview Prep Material
Buy for 40% OFF
₹9,999.00 ₹5,999.00

Data Analytics
- 20+ Live Classes & Recordings
- 24*7 Live Doubt Support
- 15+ Hands-on Live Projects
- Comprehensive Notes
- Real-world Tools & Technologies
- Access to Global Peer Community
- Interview Prep Material
- Placement Assistance
Buy for 70% OFF
₹9,999.00 ₹2,999.00
Reach Out Now
If you have any queries, please fill out this form. We will surely reach out to you.
Contact Email
Reach us at the following email address.
arun@getsdeready.com
Phone Number
You can reach us by phone as well.
+91-97737 28034
Our Location
Rohini, Sector-3, Delhi-110085